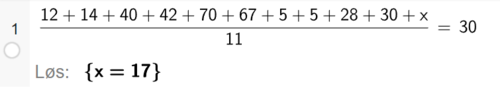2P 2025 Vår LØSNING
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
88 % av elevene deltar på undersøkelsen. Det vil si at 100 % - 88 % = 12 % ikke deltar på undersøkelsen
3 elever tilsvarer 12 %, som betyr at 1 elev tilsvarer 4 %.
100 % tilsvarer da 25 elever, fordi $\frac{100\,\%}{4\,\%}=25$
Det er 25 elever i klassen.
Oppgave 2
a)
Skriver tallene i stigende rekkefølge:
2 2 3 4 4 6 6 7 8 8
Medianen er det midterste tallet, her midt mellom 4 og 6. Medianen er 5.
Gjennomsnitt: $\frac{2 + 2 + 3 + 4 + 4 + 6 + 6 + 7 + 8 + 8}{10}=\frac{50}{10}=5$
b)
Den kumulative frekvensen for 6 personer er 7. Det betyr at 7 vogner i skiheisen hadde 6 eller færre personer om bord.
Oppgave 3
x = vekten til en liten sekk.
y = vekten til en stor sekk.
4 små sekker + 2 store sekker = 44 kg. Dette gir oss likning I:
$4x + 2y=44$
stor sekk = liten sekk + 7 kg. Dette gir oss likning II:
$y = x+7$
Løser likningssystemet ved innsettingsmetoden. Setter x+7 for y i den første likningen.
$4x + 2(x+7)=44$
$4x + 2x+14=44$
$6x=44-14$
$x=\frac{30}{6}$
$x=5$
En liten sekk veier 5 kg. Setter inn denne verdien i den andre likningen.
$y = 5+ 7 = 12$
En stor sekk veier 12 kg.
Oppgave 4
AREAL:
Areal av halvsirkel (en hel sirkel delt på 2): $\frac{\pi r^2}{2} =\frac{\pi \cdot 1^2}{2}=\frac{\pi}{2}\approx\frac{3,14}{2}$
Areal av trekant: $\frac{ g\cdot h}{2}=\frac{3\cdot 1}{2}=\frac{3}{2}$
Arealet av halvsirkelen er litt større enn arealet av trekanten.
OMKRETS:
Omkrets av halvsirkel: $r+r+\frac{2\pi r}{2}=1+1+\frac{2\cdot \pi\cdot 1}{2}=1+1+\pi\approx 5,14$
Omkrets av trekant: $AB+AC+BC=3+AC+BC>6$
Jeg vet ikke nøyaktig hvor lange sidene AC og BC er, men jeg vet at de er like lange, og at de er større enn 1,5. Dette vet jeg fordi trekanten kan deles opp i to rettvinklede trekanter, hvor hypotenusen (AC eller BC) vil være lengre enn den lengste kateten (halvparten av AB).
Omkretsen av trekanten må da være større enn 6, og dette er uansett større enn omkretsen til halvsirkelen.
Oppgave 5
a)
For å finne størrelsen på lånet, legger jeg sammen alle avdragene.
Lånet er $10\cdot 10\,000\,kr=100\,000\,kr$.
b)
Dette er et serielån fordi avdragene er like store. Terminbeløpet er høyest i starten, og går ned etter hvert som lånet nedbetales og man derfor betaler et lavere beløp i rente.
Oppgave 6
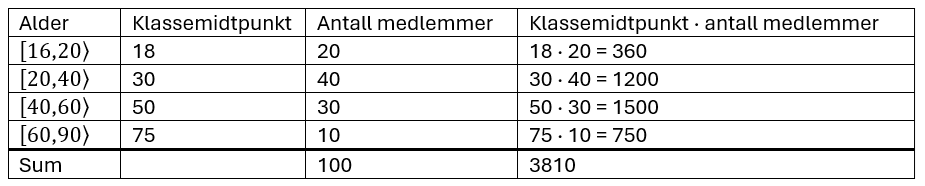
GJENNOMSNITT:
Gjennomsnittsalder: $\frac{3810}{100}=38,1$
Trine har rett i at gjennomsnittsalderen er ca. 38 år. Hun har da antatt at personene i hver klasse i gjennomsnitt har alder tilsvarende klassemidtpunktet.
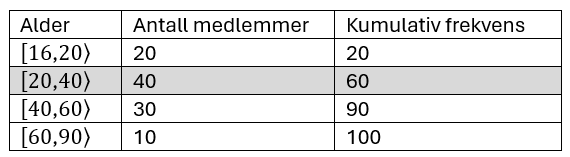
MEDIAN:
Medianen befinner seg i den klassen person nr. 50 er i, det vil si i klassen 20 til 40 år.
Person nr. 50, som befinner seg 30 personer "inn" i klassen [20,40>.
Vi antar at de 40 medlemmene fordeler seg jevnt i klassen [20,40>. Aldersforskjellen på hver person blir da 20/40=0,5 år. Person nr. 30 i klassen er 0,5*30 = 15 år "inn" i klassen, det vil si at han er 20+15=35 år.
Trine har antatt at personene sin alder fordeler seg jevnt i klassen.
Oppgave 7
En familie på 4 kaster 160 kg mat i 2025. Sofie ønsker å finne ut i hvilket år matsvinnet til en slik familie blir halvert, dersom de reduserer matsvinnet med 13 % per år.
Vekstfaktoren 0,87 angir en årlig reduksjon i avfall på 13 %.
En while-løkke beregner nytt matsvinn og nytt årstall, så lenge matsvinnet er større enn målet (halvert matsvinn).
Verdiene som blir skrevet ut forteller at i 2030, vil familien kaste ca. 79,7 kg mat.
DEL 2
Oppgave 1
a)
Planen er at prosessen som slipper ut 5000 tonn miljøskadelige stoffer per år skal redusere utslippene med 5 % per år (5000 er ganget med en vekstfaktor på 0,95). Den andre prosessen skal fortsette å slippe ut 1000 tonn per år (konstantleddet er 1000).
b)
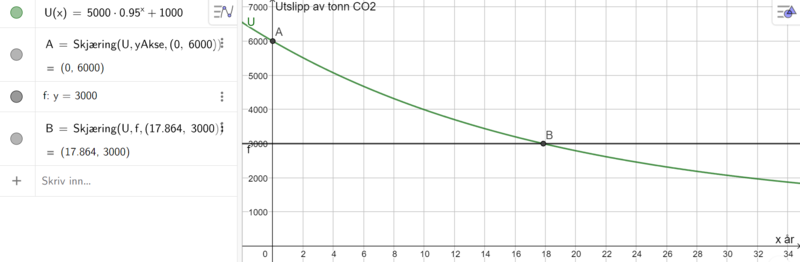
Bruker Geogebra. Finner utslippet ved start: 6000 tonn per år (se punkt A). Finner ut når utslippet har nådd 3000 tonn per år, ved å finne skjæringspunktet mellom linja y=3000 og grafen til U (se punkt B).
Utslippet er halvert etter ca. 17,9 år.
c)
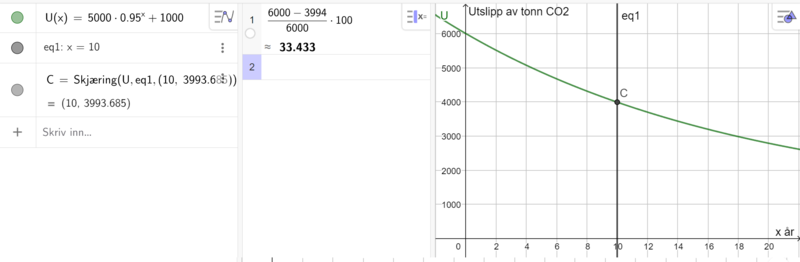
Finner utslippet etter 10 år, ved å finne skjæringspunktet mellom linja x=10 og grafen til U (se punkt C). Utslippet etter 10 år er ca. 3994 tonn per år. Bruker deretter CAS til å regne ut prosent endring i utslippene.
Etter 10 år er det årlige utslippet redusert med ca. 33,4 %.
d)
Bedriften har ikke planlagt å redusere utslippet til prosessen som slipper ut 1000 tonn miljøskadelige stoffer per år (konstantleddet er 1000). Det vil derfor være umulig for bedriften å fylle kravet om utslipp på 800 tonn per år.
Oppgave 2
PÅSTAND 1
Det er ikke sikkert medianalderen endres dersom det kommer en ny person inn i rommet. Dersom personen er akkurat like gammel som medianalderen, vil ikke medianen endres. Dersom personen er yngre eller eldre enn medianalderen, vil medianen derimot endres.
PÅSTAND 2
Bruker CAS i Geogebra.
Gjennomsnittsalderen kan bli 30 år dersom det kommer inn en person på 17 år.
Oppgave 3
a)
Trekant ABC og trekant ADE har har parvis like store vinkler, og er derfor formlike.
Vinkel ADE = vinkel ABC = 90 grader (dette er merket på figuren).
Vinkel A er felles i begge trekanter (og da selvfølgelig like stor i begge trekanter).
Vinkel BCA og vinkel DEA er samsvarende vinkler, og derfor også like store.
b)
For å finne avstanden fra B til D, kan vi først regne avstanden fra A til B, og trekke fra avstanden fra A til D.
AD er halvparten av DE, så AB må være halvparten av BC, siden trekantene er formlike. Det vil si at AB = 20 m.
$BD = AB - AD = 20 - 5 = 15$
Avstanden fra B til D er 15 m.
Oppgave 4
a)
Vi kan løse oppgaven enten ved regresjon i Geogebra, eller ved regning.
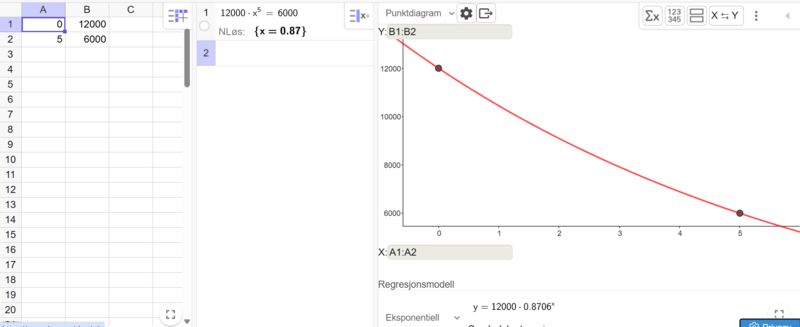
Ved regresjon, legger jeg inn opplysningene i regenarket i Geogebra (se bilde), og bruker "regresjonsanalyse" og velger eksponentiell modell. Jeg får da modellen $y=12000\cdot 0,87^x$.
Ved regning bruker jeg CAS til å finne vekstfaktoren som halverer antall fugler etter 5 år (se bildet). Jeg løser likningen $12000\cdot x^5=6000$, og finner at vekstfaktoren må være 0,87.
b)
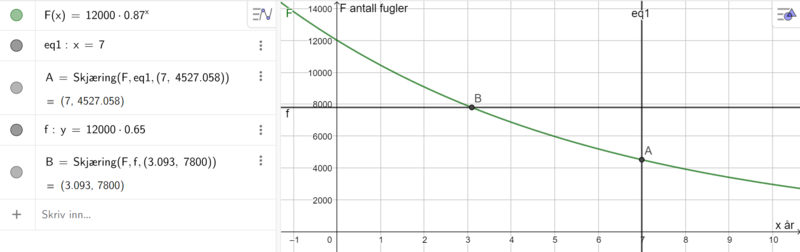
Finner skjæringspunktet mellom linja x=7 og grafen til F. Det vil være 4527 fugler om 7 år ifølge modellen (se punkt A).
c)
En reduksjon på 35 % gir en vekstfaktor på 0,65. Finner skjæringspunktet mellom linja $y=12000\cdot 0,65$ og grafen til F (se punkt B på bildet over). Det vil gå 3 år før bestanden er redusert med 35 % ifølge modellen.
Oppgave 5
a)
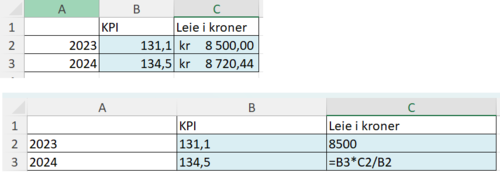
Bruker Excel til å beregne ny maksimal husleie i 2024, dersom husleia fulgte utviklingen til konsumprisindeksen.
Husleien kunne maksimalt vært satt til 8720,44 kroner i 2024, så huseieren hadde ikke lov til å sette opp husleia til 9000 kr i 2024.
b)
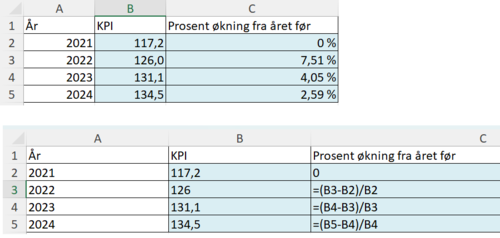
Bruker Excel til å lage en oversikt som viser hvor mange prosent konsumprisindeksen økte med per år fra oktober 2021 til oktober 2024.
c)
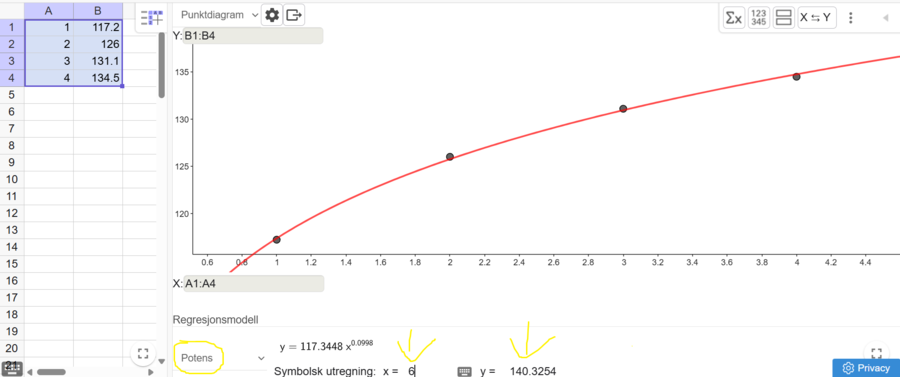
Det er litt vanskelig å forutsi hvordan KPI vil endre seg i årene fremover, da økonomien avhenger av hvordan verdensbildet endrer seg. Hvis vi likevel skal det, utfører jeg en regresjonsanalyse basert på de KPI'ene jeg har, og finner at en potensmodell passer godt til punktene. Jeg skriver inn x=6 (for 2026) i vinduet for regresjonsanalyse, og får opp y=140,3. Dette er ifølge modellen verdien for KPI i 2026. Jeg bruker deretter denne KPI'en til å beregne husleien i 2026, dersom den følge KPI-utviklingen.
Husleien i 2026 kan være på ca. 9096 kr per måned.
Oppgave 6
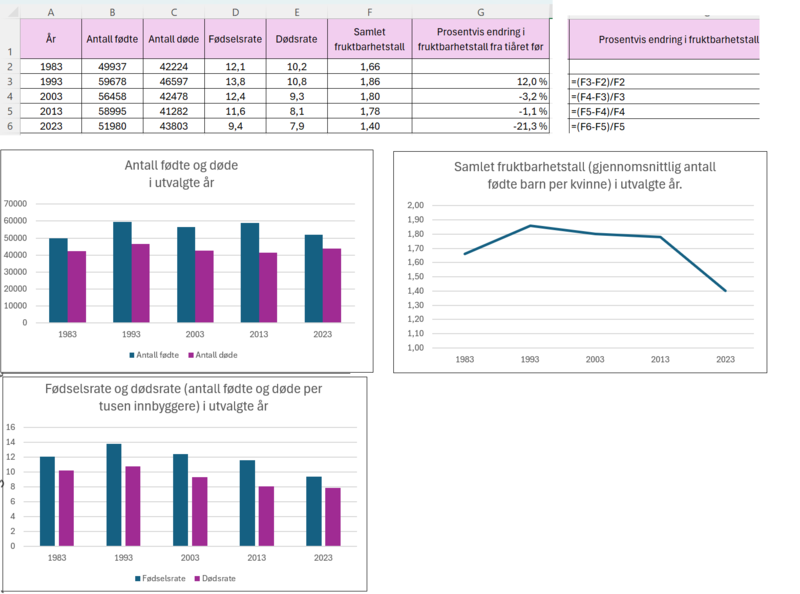
Bruker Excel til ulike fremstillinger. Her velger seg søylediagrammer som viser fødselstall og dødstall sammen. Dette blir selvfølgelig et veldig likt diagram som å vise fødselsrate og dødsrate. Jeg velger et linjediagram for å vise utviklingen i fruktbarhetstall, og viser prosentvis endring i fruktbarhetstall i Excel. Det er mange flere beregninger man kan gjøre, dette er bare et utvalg.
