Fortegnsskjema
Et fortegnsskjema kan være nyttig i flere sammenhenger, som for eksempel ved drøfting av funksjoner eller ved løsing av ulikheter.
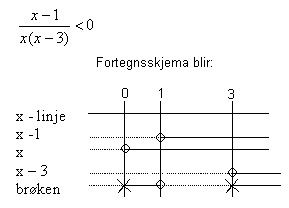
Eks:
Vi har ulikheten:
Fra fortegnsskjemaet ser man hvor brøkens faktorer er negative og positive og man kan lese direkte fra skjemaet for hvilke x verdier ulikheten er oppfylt. Stiplet linje representerer negative verdier og heltrukket linje positive verdier.
Fra fortegnsskjemaet ser man at brøken er mindre enn null for x verdier mindre enn null og i intervallet en til tre. Merk at brøken ikke er definert for x lik null, eller x lik tre. Løsningen på ulikheten blir altså:
<math> x \in < \leftarrow , 0 > \cup < 1, 3 > </math>
På samme måte kan man trekke opp skjema for funksjoner og deriverte for å få oversikt over funksjonens oppførsel.