Funksjonen a sin cx + b cos cx
Vi ønsker å skrive funksjonen f(x)= a sin cx + b cos cx på formen g(x)= A sin (cx +$\varphi$). Det er alltid mulig.
Altså: a sin cx + b cos cx = A sin (cx + $\varphi$)
$A = \sqrt{a^2 + b^2}$ og $tan \varphi = \frac ba$
NB: $\varphi$ ligger i samme kvadrant som punktet (a, b)
Eksempel:
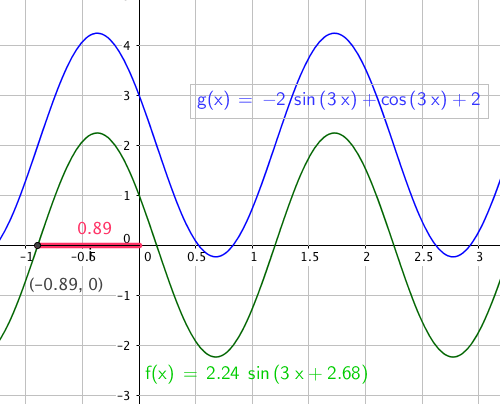
f(x) = -2 sin 3x + cos 3x $\quad \quad A= \sqrt{(-2)^2 + 1^2} = \sqrt 5 = 2,24 \quad \quad tan \varphi = - \frac 12 \Rightarrow \varphi = 2,678$
Husk at punktet (-2,1) ligger i andre kvadrant, så vi jakter på en vinkel i denne kvadranten.
Vi får : f(x)= 2,24 sin(3x + 2,,678)
Her er utgangsfunksjonen, her kalt g(x) tegnet med likevektslinje y = 2, bare for å kunne sammenligne grafene til de to uttrykkene. Vi ser at de er identiske, med en faseforskyvning mot venstre på $ \frac{2,678}{3} = 0,89$.
Bevis