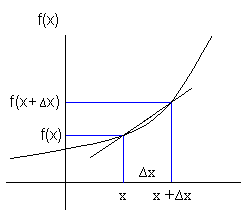Funksjoner II
Gjennomsnittlig vekst
Gjennomsnittlig vekst refererer til den jevne eller gjennomsnittlige økningen (eller reduksjonen) i en verdi over en bestemt tidsperiode. Dette konseptet brukes ofte i matematikk, økonomi og naturfag for å forstå utviklingen over tid, og det gir et mål på hvordan en variabel forandrer seg i gjennomsnitt mellom to punkter.
Matematisk beregnes gjennomsnittlig vekst ved hjelp av formelen:
\[ \text{Gjennomsnittlig vekst} = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1} \]
Her er:
\( y_1 \) og \( y_2 \): verdier ved to forskjellige tidspunkter \( x_1 \) og \( x_2 \),
\( \Delta y \): forskjellen mellom de to verdiene,
\( \Delta x \): forskjellen mellom de to tidspunktene.
Eksempel 1:
Gjennomsnittlig vekst i et tre
La oss si at et tre er 2 meter høyt når det blir plantet, og etter 5 år har det vokst til en høyde på 7 meter. Vi ønsker å finne ut hva den gjennomsnittlige veksten per år er.
Steg 1: Identifiser verdiene
Startverdi (\( y_1 \)): 2 meter (ved \( x_1 = 0 \), altså år 0).
Sluttverdi (\( y_2 \)): 7 meter (ved \( x_2 = 5 \), altså år 5).
Steg 2: Beregn forskjellene
\( \Delta y = y_2 - y_1 = 7 - 2 = 5 \) meter.
\( \Delta x = x_2 - x_1 = 5 - 0 = 5 \) år.
Steg 3: Sett inn i formelen
\[ \text{Gjennomsnittlig vekst} = \frac{\Delta y}{\Delta x} = \frac{5 \, \text{meter}}{5 \, \text{år}} = 1 \, \text{meter per år}. \]
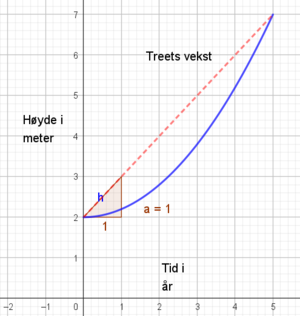
Tolkning: Det betyr at treet har vokst i gjennomsnitt 1 meter per år over de fem årene. Den blå grafen viser modellen for vekst. Vi ser at treet vokser sakte i starten, og at vekstfarten øker etter hvert. Den røde stiplede linjen viser den gjennomsnittlige vekstfarten i perioden 0 til 5 år.
Dersom vi trenger å vite hva veksten var på et gitt tidspunkt, bruker vi det som kalles for momentan vekst.
Gjennomsnittlig vekst gir en enkel måte å forstå endring over tid på, selv om veksten i virkeligheten kanskje ikke har vært helt jevn. Dette gjør konseptet nyttig i alt fra biologiske studier til økonomiske analyser.
Momentan vekst
Den momentane veksten i et punkt er det samme som den deriverte i punktet.
Momentan vekst refererer til vekstraten i et bestemt øyeblikk i stedet for gjennomsnittet over en periode. Der gjennomsnittlig vekst måler endringen mellom to punkter, beskriver momentan vekst hva som skjer "akkurat nå". Matematikere bruker den deriverte til å beregne momentan vekst, som er et sentralt konsept i kalkulus.
Matematisk kan momentan vekst defineres som grensen for gjennomsnittlig vekst når tidsintervallet \( \Delta x \) nærmer seg 0. Dette skrives som:
\[ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]
Her er:
- \( f'(x) \): den momentane vekstraten,
- \( f(x) \): funksjonsverdien (f.eks. høyden på et tre, en mengde penger, eller en annen variabel),
- \( \Delta x \): et lite tidsintervall.
Den deriverte av en funksjon beskriver hastigheten funksjonene forandrer seg med, med hensyn på en uavhengig variabel. Den deriverte er også stigningen til tangenten av kurven. La oss anta at vi har funksjonen f(x) i et koordinatsystem. Vi velger et punkt x på førsteaksen. Tilhørende funksjonsverdi er f(x). La oss tenke oss at vi beveger oss et lite stykke bortover på førsteaksen fra x. Denne avstanden kaller vi ∆x. Dette nye punktet på førsteaksen heter da x+∆x. Funksjonsverdien til dette punktet blir f(x+∆x).
Gjennomsnittlig vekst gir et mål på endringen over en periode, mens momentan vekst forteller oss hvor raskt verdien endrer seg på et spesifikt tidspunkt. For å forstå forskjellen kan vi sammenligne det med å kjøre bil: gjennomsnittshastigheten forteller hvor raskt du har kjørt i gjennomsnitt over hele turen, mens momentan hastighet forteller hvor raskt du kjører på et spesifikt tidspunkt – som målt med en fartsmåler.
Eksempel 2:
Momentan vekst av et tre
La oss si at høyden til et tre \( h(t) \) (i meter) er gitt av funksjonen \( h(t) = 0,2t^2 + 2 \), der \( t \) er tiden i år. Vi ønsker å finne den momentane vekstraten (veksthastigheten) etter \( t = 1 \) år, og etter \(t =4,5\) år. (Dette er samme treet som vi så på i gjennomsnittlig vekst.)
Steg 1: Finn den deriverte av \( f(t) \)
Den momentane vekstraten er gitt av den deriverte \( f'(t) \). Deriver funksjonen: \[ f'(t) =( 0,2t^2 + 2)' = 0,4t \]
Steg 2: Beregn \( f'(t) \) ved \( t = 1 \) og \( t=4,5\)
Sett inn i \( f'(t) \):
\[
f'(1) = 0,4 \cdot 1 = 0,4
\]
\[
f'(4,5) = 0,4 \cdot 4,5 = 1,8
\]
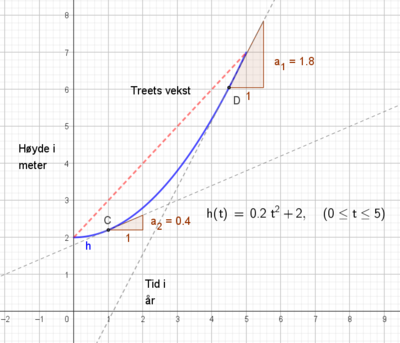
Tolkning: Den momentane vekstraten etter 1 år er 0,4 meter per år. Det betyr at treet vokser med en hastighet på 0,4 meter per år akkurat på dette tidspunktet. Etter 4,5 år er veksten bedre, da er den 1,8 m/år. Legg merke til at den deriverte i punktene er stigningstallet til tangenten i det respektive punkt.
Sammenligning med gjennomsnittlig vekst
Hvis vi sammenligner dette med gjennomsnittlig vekst mellom \( t = 0 \) og \( t = 5 \), så vi at den var 1,0 m/år. Det er en grei informasjon dersom vi ikke er interessert i detaljene i vekstforløpet, men bare gjennomsnittet mellom start og stopp punkt. Skal man si noe mer detaljert om veksten er ofte momentan vekst egnet til det.
Dersom man ikke har et funksjonsuttrykk, men bare en graf kan man likevel finne gode verdier for både gjennomsnittlig vekst og momentan vekst.
For gjennomsnittlig vekst: Merk av start og sluttpunkt på grafen. Legg en linjal over og tegn den rette linjen mellom punktene. Finn stigningstallet til den rette linjen. Det er den gjennomsnittlige veksten.
For momentan vekst: Merk av punktet på grafen. Legg en linjal i flukt med grafen, slik at den kun tangerer grafen i det avmerkede punktet ( vanskelig å få nøyaktig dersom figuren er liten).Tegn den rette linjen og finn stigningstallet.
Derivasjon ved bruk av definisjonen
Vi har funksjonen
\[f(x) = x^2-2x+1 \]
og definisjonen
\[f'(x) = \lim_{\Delta x\to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]
Vi setter funksjonen inn i definisjonen:
\[f'(x) = \lim_{\Delta x\to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]
\[f'(x) = \lim_{\Delta x\to 0} \frac{(x+\Delta x)^2 - 2(x + \Delta x) +1 - (x^2-2x + 1)}{\Delta x} \]
\[f'(x) = \lim_{\Delta x\to 0} \frac{x^2+2x\Delta x + (\Delta x)^2 - 2x - 2\Delta x + 1 - x^2 +2x - 1}{\Delta x} \]
\[f'(x) = \lim_{\Delta x\to 0} \frac{2x\Delta x + ( \Delta x)^2 - 2\Delta x}{\Delta x} \]
\[f'(x) = \lim_{\Delta x\to 0} \frac{ \Delta x(2x +\Delta x-2)}{\Delta x} \]
\[f'(x) = \lim_{\Delta x\to 0} 2x + \Delta x - 2 \]
\[f'(x) = 2x - 2 \]
Nå slipper vi vanligvis å bruke definisjonen når vi deriverer, fordi vi har et sett med derivasjonsregler som gjør det lettere.
Derivasjonsregler
Polynomfunksjoner
Den deriverte av en konstant er null. Vi deriverer ledd for ledd. En potens med grunntall x deriveres slik:
\[ f(x) = k, \quad \quad f'(x) = 0 \]
\[ f(x) = x^n, \quad \quad f'(x) = nx^{n-1}\]
\[ f(x) = kx^n, \quad \quad f'(x) = nkx^{n-1}\]
\[ f(x) = g(x) + h(x) + ..., \quad \quad f'(x) = g'(x) + h'(x) + ....\]
Eksempel 3:
\[ f(x) = x^4- 3x^2 + 3x - 1 \]
\[ f'(x) = 4x^3- 6x + 3 \]
I det første leddet trekkes fire ned foran x og eksponenten reduseres med en. I det andre leddet multipliseres 2 med faktoren som allerede står foran x. I ledd nr tre deriverer vi x og får 1, altså blir det 3 ganger 1 som er 3. Det siste leddet er -1, det er en konstant og den deriverte er da null.
Funksjoner med kvadratrot og n'te røtter
Funksjoner som inneholder
\[ \sqrt{x} \quad eller \quad \sqrt[m]{x^n} \] skrives om til \[ x^{\frac 12} \quad eller \quad x^{\frac nm} \]
Derivasjons regelen for potenser med x som grunntall (over) Gjelder
\[ f(x) =\sqrt{x}, \quad \quad \quad \quad f'(x)= (\sqrt{x})' = ( x^{\frac 12})' = \frac12 x^{- \frac 12} = \frac{1}{2 \sqrt{x}} \]
\[ f(x) =\sqrt[m]{x^n}, \quad \quad \quad \quad f'(x)= (\sqrt[m]{x^n})' = ( x^{\frac nm} )' = \frac nm x^{ \frac nm - 1} \]
Eksempel 4:
\[ g(x) = 4 \sqrt{x} - \sqrt[6]{x^{5}} \]
\[ g'(x) = 4 \cdot \frac{1}{2 \sqrt{x}} - \frac 56 x^{ \frac 56 - 1} \]
Da er derivasjonen gjort, så er det å rydde opp litt:
\[ g'(x) = \frac{4}{2 \sqrt{x}} - \frac 56 x^{ -\frac 16} = \frac{2}{ \sqrt{x}} - \frac{5}{6 \sqrt[6]{x}} \]
Logaritme- og eksponential funksjoner
\[ f(x)= \ln|x|, \quad \quad \quad f'(x) = \frac 1x \]
\[ g(x)= e^x, \quad \quad \quad g'(x) = e^x \]
\[ h(x) = a^x \quad \quad \quad h'(x) = a^x \cdot ln a \]
Trigonometriske funksjoner
\[ f(x) = \sin(x), \quad \quad \quad f'(x) = \cos(x) \]
\[ f(x) = \cos(x), \quad \quad \quad f'(x) = -\sin(x) \]
\[ f(x) = \tan(x), \quad \quad \quad f'(x)=\frac{1}{cos^2x} \quad eller \quad f ' (x)= 1 + tan^2x \]
Til nå har vi sett hvordan enkle funksjoner har sine deriverte, men vi trenger noen metoder for sammensatte funksjoner som brøkfunksjoner, produkt av funksjoner, og funksjoner inne i en funksjon:
Produktregelen
\[ f(x) = g(x) \cdot h(x), \quad \quad \quad f'(x) = g'(x) \cdot h(x) + g(x) \cdot h'(x) \]
Eksempel 5:
\[ f(x) = x^4 \ln|x| \]
\[ f'(x) = 4x^3 \cdot \ln|x| + x^4 \cdot \frac 1x = x^3( 4 \ln|x| + 1) \]
Brøkfunksjoner
\[ f (x)=\frac{g(x)}{h(x)}, \quad \quad \quad f ' (x)= \frac{g'(x)\cdot h(x)- g(x)\cdot h'(x)}{(h(x))^2} \]
Kjerneregelen
\[ f(x) = g(u(x)), \quad \quad \quad f'(x) = g'(u) \cdot u'(x) \]
Eksempel 6:
\[ f(x) = (x^2- \sqrt{x})^3 \] Setter $ u = x^2- \sqrt{x} $ og får \[ f'(x) = 3u^2 \cdot (2x - \frac{1}{2 \sqrt{x}}) = 3 (x^2- \sqrt{x})^2 \cdot (2x - \frac{1}{2 \sqrt{x}}) \]
Praktisk anvendelse av derivasjon
Grensekostnader
En kostnadsfunksjon uttrykker hva det koster å produsere x enheter av en vare.
Grensekostnaden forteller hvor mye kostnaden øker dersom man øker produksjonen fra x enheter til x+1 enheter.
Grensekostnaden er tilnærmet lik den deriverte av kostnadsfunksjonen
Eksempel 7:
Kostnaden ved produksjon av en vare er gitt som:
\[K(x) = 0,002x^2 + 30x +2000, x \in [ 0, 3000]\]
Der x er antall enheter.
Den deriverte av K(x) er:
\[K’(x) = 0,004x + 30 \]
Man produseres 500 enheter og ønsker å finne økningen i kostnader når produksjonen økes til 501 enheter: \[K’(500) = 0,004 · 500 + 30 = 32 \]
Det vil koste ca. 32 kroner å øke produksjonen fra 500 til 501 enheter.
Kostnaden ved å produsere henholdsvis 500 og 501 enheter er:
\[K(500) = 0,002 · 500 2 + 30 · 500 + 30 = 15.530kr. \]
\[K(501) = 0,002 · 501 2 + 30 · 501 + 30 = 15.562,002kr.\]
Man ser at nøyaktigheten ved å bruke den deriverte er god. Nøyaktigheten er størst når grafen krummer lite.
Kostnadsfunksjonen er en matematisk modell og vil trolig ikke gi det helt riktige bildet a virkeligheten. Derfor kan man bruke K’(x) når man skal finne grensekostnaden. Feilen er liten og regningen enklere.
Grenseinntekter
Dersom inntekten ved salg av et produkt er I(x) der x er solgte enheter er grenseinntekten I’(x). Grenseinntekten forteller hvor mye inntektene øker når salget øker fra x til x+1 enheter.
Overskudd
En virksomhets overskudd er inntekter minus kostnader.
\[O(x) = I(x) – K(x) \]
Overskuddet er størst når O’(x) = 0,
vi får:
\[O’(x) = I’(x) – K’(x)\]
\[O’(x) = 0\]
\[I’(x) – K’(x) = 0 \]
\[I’(x) = K’(x)\]
- Når grensekostnadene er lik grenseinntektene er overskuddet størst.
Eksempel 8:
En bedrift har muligheten til å produsere 3000 enheter av et produkt. Hvor mange enheter må produseres for å maksimalisere overskuddet?
$ x \in [ 0, 3000] $
Kostnadsfunksjonen er gitt som: $K(x) = 0,002x^2 + 30x +2000 $
$K’(x) = 0,004x + 30 $
Inntektsfunksjonen er gitt som: $I(x) = 0,0001x^2 + 40x$
$I’(x) = 0,0002x + 40 $
$K’(x) = I’(x)$
$0,004x + 30 = 0,0002x + 40$
$x = 2632$
Bedriften får størst overskudd ved å produsere 2632 enheter.
Maksimums og minimums problemer
Derivasjon er et egnet verktøy når man arbeider med maksimering eller minimering fordi den deriverte til funksjonen er null i et maksimumspunktet og minimumspunktet til funksjonen.
\[f’(x) = 0 \]
- gir deg alltid x verdien i et maksimums eller minimumspunkt, dersom de finnes.
Eksempel 9:
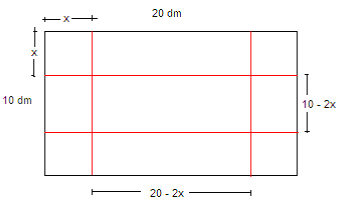
Du har en aluminiumsplate på en ganger to meter og ønsker å forme den til en boks med størst mulig volum.
Volumet av boksen er:
\[V(x) = bhl = x(20-2x)(10-2x) = x(200 – 40x – 20x +4x^2) = 4x^3 – 60x^2 +200x \]
\[V’(x) = 12x^2 – 120x +200 \]
Setter den deriverte lik null:
\[V’(x) = 0 \]
\[12x^2 – 120x + 200 = 0 \]
x = 2,1 (tolkning av svarene fører til at vi forkaster den andre muligheten)
Det betyr at boksen får et størst volum dersom den har en høyde på 21 cm.
Eksempel 10:
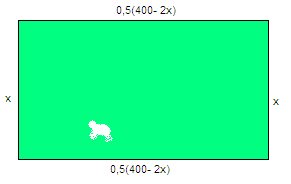
En bonde har en sau og 400 meter gjerde. Hun lurer på hvordan hun kan få det største arealet for sauen, ved å lage en innhegning som er firkantet.
Løsning:
Areal:
\[A(x) = x(200 – x) = 200x – x^2 \]
Den deriverte av arealet:
\[A’(x) = 200 – 2x \]
Setter A’(x) = 0 og får
x = 100
Altså er det et kvadrat som gir størst areal.
Strekning, fart og akselerasjon
Et legeme tilbakelegger strekningen s i løpet av tiden t gitt ved s(t)
Legemets fart v er gitt som $v(t) = s'(t)$
Farten er den deriverte av strekningen.
Legemets akselerasjon a er gitt som
$a(t) = v'(t) = s''(t) $
- Vi har følgende sammenheng mellom strekning, fart og akselerasjon:
\[ s''(t) =v'(t) = a(t)\]
Akselerasjonen er den deriverte av farten, dvs. den dobbelderiverte av strekningen.
Eksempel 11:
En partikkel forflytter seg etter $s(t) = 3,7t^2 $
Hvor langt forflytter partikkelen seg på 6 sekunder?
$s(6) = 3,7 · 6^2 = 133,2m $
Hva er partikkelen fart etter 4 sekunder?
$v(t) = s'(t) = 7,4t $
$v(4) = s'(4) =7,4 · 4 =29,6 m/s $
Hvor lang tid tar det før partikkelen beveger seg med 100 m/s?
v(t) = 100 m/s gir
100m/s = 7,4t,
t =100/7,4 = ca. 13,5s
Hva er partikkelens akselerasjon? Er akselerasjonen konstant, eller varierer den med tiden?
$a(t) = v'(t) = 7,4m/s^2$ Man observerer at t ikke inngår i uttrykket for akselerasjonen, hvilket betyr at den er konstant $7,4 m/s^2$, gjennom hele tidsforløpet.
Fortegnsskjema
Et fortegnsskjema kan være nyttig i flere sammenhenger, som for eksempel ved drøfting av funksjoner eller ved løsning av ulikheter. Heltrukket linje representerer positive verdier. Stiplet linje representerer negative verdier
Eksempel 12:
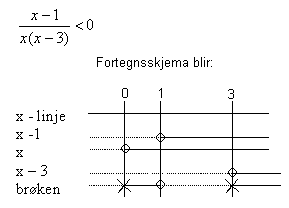
Vi har ulikheten:
Fra fortegnsskjemaet ser man hvor brøkens faktorer er negative og positive og man kan lese direkte fra skjemaet for hvilke x verdier ulikheten er oppfylt. Stiplet linje representerer negative verdier og heltrukket linje positive verdier.
Fra fortegnsskjemaet ser man at brøken er mindre enn null for x verdier mindre enn null og i intervallet en til tre. Merk at brøken ikke er definert for x lik null, eller x lik tre. Løsningen på ulikheten blir altså: <math> x \in < \leftarrow , 0 > \cup < 1, 3 > </math>
Eksempel 13:
På samme måte kan man trekke opp skjema for funksjoner og deriverte for å få oversikt over funksjonens oppførsel.
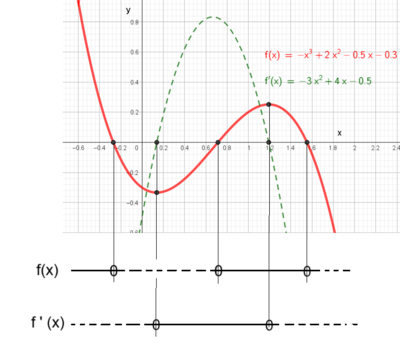
Eksempel 14:
Skisser grafen ut fra fortegnslinjene til funksjonen og funksjonens deriverte:
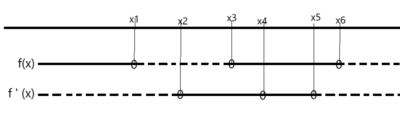
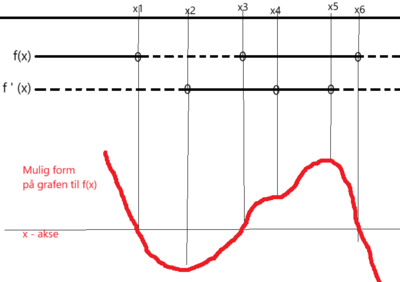
Funksjonen er positiv fram til x1, grafen ligger over x aksen. Grafen synker fram til x2, der den deriverte skifter fortegn. Funksjonen har et minimumspunkt. Funksjonen vokser og kommer over x aksen etter x3. Den fortsetter å vokse til x4, hvor den flater ut og grafen får et terasssepunkt. Etter x4 er den deriverte fortsatt positiv, så grafen vokser til x5 hvor funksjonen når et maksimumspunkt. Den deriverte skifter fortegn, er nå blitt negativ og grafen synker mot nullpunktet i x6. Etter det fortsetter den å avta. Grafen kan ha en form som den nedenfor:
Funksjonsdrøfting
Funksjonsdrøfting er analytiske undersøkelser av funksjonen og ender ofte opp med at vi skisserer (tegner) grafen i et koordinatsystem. I en tid med grafiske kalkulatorer og software for alle mulige analyser kan man jo spørre seg om nødvendigheten og viktigheten av å kunne gjøre dette "manuelt"? Svaret, etter vår mening, er at kalkulator og PC kan hjelpe deg til å få en økt forståelse og er glimrende verktøy, men kun en manuell gjennomgang viser om du har forstått emnet. Nedenfor følger en liste over ting du bør få klarhet i før du tegner grafen til funksjonen. Enkelte punkter kan det være vanskelig å få oversikten over, da går du videre til neste punkt. Vi kaller funksjonen f.
- Finn definisjonsmengden til f og finn eventuelle asymptoter.
- Finn eventuelle nullpunkter til f. f(x) = 0
- Finn punktet der grafen krysser Y aksen. f(0) = ?
- Finn $f'(x)$, finn eventuelle nullpunkter og drøft fortegnet til den deriverte.
- Finn $f''(x)$, finn eventuelle nullpunkter og drøft fortegnet til den dobbelderiverte.
- Se etter mulig symmetri.
Funksjonsutrykket f(x)
\[f(x) = 0 \] Løsningene av ligningen gir alle funksjonens nullpunkter (der grafen krysser x aksen).
Eksempel 15:
En funksjon er gitt som $f(x) = x^3 +2x^2-x-2$
Finn nullpunktene til f.
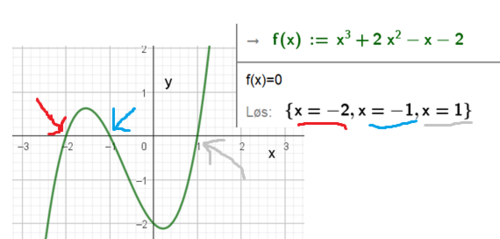
Her er CAS brukt i løsningen. Dersom du skal løse den for hånd må du faktorisere f. Det er naturlig å prøve divisjon med (x+1) eller (x-1). Du vil se at begge fører fram og du kommer til at f også kan skrives som $f(x) = (x+1)(x-1)(x+2)$. På faktorisert form ser man nullpunktene direkte.
Den deriverte f’(x)
\[f ’(x) = 0 \] Løsningen av ligningen gir x verdiene for maksimums- eller minimumspunkter til f, også kalt ekstremalpunkter.
Dersom f’(x) er positiv vokser f(x). Er f’(x) negativ avtar f(x). Grafen til f’(x) viser vekstforløpet til f(x). For å avgjøre om et ekstremalpunkt er et toppunkt eller et bunnpunkt lager man et fortegnsskjema. For å få med alle funksjonens ekstremalpunkter må man også sjekke punkter der funksjonen ikke er deriverbar, som knekkpunkter og endepunkter.
Eksempel 16:
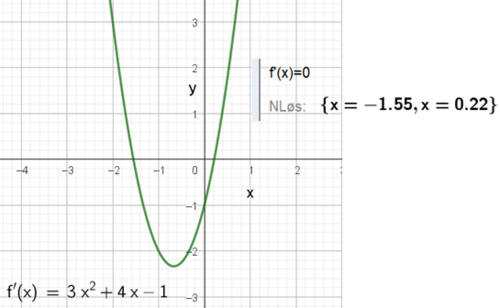
Nullpunktene til den derivert funksjonen gir oss x verdien til ekstremalpunktene til f, fra eksempel 15. Vi observer et den deriverte skifter fra å være positiv til å bli negativ rundt x = -1,55. Det betyr at f har et toppunkt for x = -1,55. Dersom vi setter inn finner vi : f(-1,55) = 0,63. Punktet (-1.55 , 0.63) er altså et ekstremalpunkt, nærmere bestemt et toppunkt eller et maksimumspunkt. Funksjonen har også et minimumspunkt.
Funksjonsverdiene til den deriverte utrykker stigningstallene til tangenter til f, for alle x verdier
Den dobbelderiverte f’’(x)
\[f’’(x) = 0 \] Løsningen av ligningen gir vendepunktet(ene) til f.
Dersom den dobbelderiverte er en konstant har f ingen vendepunkter. Dersom den dobbelderiverte er negativ krummer grafen sin hule side nedover. Er den dobbelderiverte positiv vender grafen sin hule side oppover.
Eksempel 17:
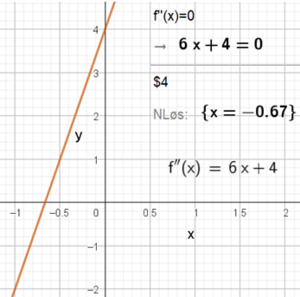
Figuren viser den dobbelderiverte til funksjonen f i eksempel 15. Funksjonen har et vendepunkt for x = -0,67. For mindre x verdier er den dobbelderiverte til f negativ, og f vender sin hule side nedover. For x verdier større enn -0,67 er den dobbelderiverte positiv og f vender sin hule side oppover.
Eksempel 18:
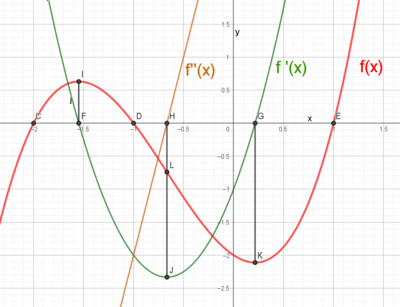
Figuren nedenfor prøver å sammenfatte betydningen av eksemplene 15, 16 og 17. C, D og E er nullpunktene til f. F og G er nullpunktene til f' og forteller at funksjonen har et toppunkt for x = F, i I, og et bunnpunkt for x= G, i K. Den dobbelderiverte er null i H som gir f ' et bunnpunkt i J, men viktigere: et vendepunkt i L. Vendepunkter forteller at grafen skifter fra å vende sin hule side nedover, til å vende den hule siden oppover etter x = L. Det kan vi si fordi når den dobbelderiverte er positiv vender funksjonen sin hule side oppover, og når den dobbelderiverte er negativ vender grafen til f sin hule side ned.
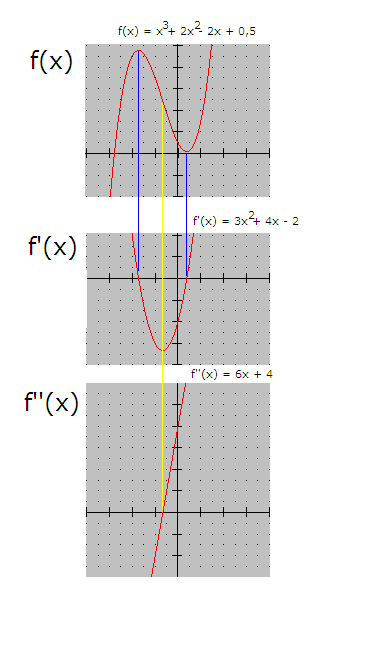
Nedenfor har vi illustrert de samme relasjonene, men med en litt annen funksjon og etter hverandre, i stedet for alle grafer i ett diagram.
Eksempel 19:
La oss se på et eksempel, uten hjelpemidler:
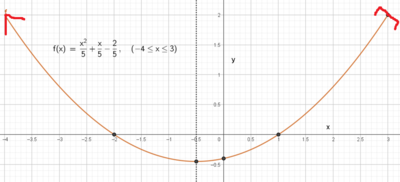
Funksjonen f er gitt ved \[f(x) = \frac{x^2}{5} +\frac{x}{5} - \frac{2}{5}, \quad x \in <-4, 3] \].
a) Finn likningen for symmetrilinjen.
b) bruk symmetrilinjen til å finne eventuelle ekstremalpunkter til f.
c) Hva er skjæringspunktet mellom grafen til f og andreaksen?
d) Bestem nullpunktene til f.
e) Finn verdimengden til f.
f) Finn f'(x). Hva utrykker denne?
g) Finn f'(1). Hva betyr svaret du får?
h) Finn et uttrykk for tangenten til f i punktet (1, f(1))
i) Ett punkt på grafen har en tangent med stigningstall -0,2. Finn likningen til denne tangenten.
j) f har ikke noen vendepunkter. Forklar det ut fra den dobbelderiverte til f. Hva kan du si om f ut fra den dobbelderiverte?
Løsning:
a) Symmetrilinje:
\[ x = \frac{-b}{2a} = \frac{- \frac 15}{2 \cdot \frac 15} = - \frac 12 \], altså $x = - 0,5 $
b) Ekstremalpunkt:
\[ f( - \frac 12) =\frac{(- \frac 12)^2}{5} +\frac{- \frac 12}{5} - \frac{2}{5} = \frac{1}{20} - \frac {1}{10} - \frac 25 = - \frac {9}{20} \]
Koeffisienten foran 2. grads leddet er positiv, hvilket betyr at grafen vender sin hule side opp, vi har et minimumspunkt (bunnpunkt) med koordinater $( - \frac 12, - \frac{9}{20}) $
c) Skjæring med y-akse:
x = 0 :\[f(0) = - \frac 25\]
d) Nullpunkt:
\[ f(x)=0 \] \[ \frac{x^2}{5} + \frac x5 - \frac 25 = 0 \] \[ x= \frac{- \frac 15 \pm \sqrt{(- \frac 15)^2- 4 \cdot \frac 15 \cdot \frac 25}}{2 \cdot \frac 15}\] \[ x= \frac{- \frac 15 \pm \frac 35}{\frac 25} \] \[ x = \frac{-1 \pm 3}{2} \] \[x = -2 \vee x = 1\]
e) Verdimengde. Vi ser at funksjonen er definert for x=3, den er kontinuerlig i definisjonsområdet og den har et minimum for x = - 0,5. Verdimengden må da bli fra f(-0,5) til f(3):
\[ f(3) = \frac 95 + \frac 35 - \frac 25 = 2 \]
Verdimengde: \[V_f = [ - \frac {9}{20}, 2]\]
Funksjonen har altså ett ekstremalpunkt til, for x =3, et maksimum med verdien 2.
f) Bruker regelene for derivasjon av polynomfunksjoner og får:
\[ f'(x) = \frac 25 x + \frac 15 \]
Det er en funksjon som gir oss stigningstallet til tangentene til funksjonen for alle forskjellige x- verdier.
g)
\[ f'(1) = \frac 25 \cdot 1 + \frac 15 = \frac 35, \quad (eller \quad 0,6) \]
Det betyr at den momentane veksten i 1 er 0,6, altså når x= 1 er endringen i y verdi 0,6. Momentan fordi det er bare i x= 1.
h) Vi skal finne likningen for tangenten i (1, f(1)). Vi kjenner stigningstallet fra oppgave g, og vi har punktet (1,0) fra oppgave d:
\[y = ax + b \] \[0 =0,6 \cdot 1 +b \] \[b = -0,6\]
Likningen til tangenten blir da:
\[ y=0,6x - 0,6 \]
i)
Vi vet at f'(x) er et uttrykk for stigningstallet til tangenten til f, så vi setter f'(x) = - 0,2, for å finne den ønskede x verdi.
\[ f'(x) = -0,2 \] \[ \frac 25 x + \frac 15 = -0,2 \]
gjør - 0,2 om til brøk:
\[ \frac 25 x + \frac 15 = - \frac 15 \]
\[ x = -1 \]
Vi finner y verdien til punktet:
\[ f(-1) = \frac{(-1)^2}{5} + \frac {-1}{5} - \frac 25 = - \frac 25 = -\frac{4}{10} = - 0,4 \]
Finner b når vi har stigningstallet a= -0,2 og punktet (-1, -0,4):
\[y = ax + b \]
\[-0,4 = -0,2 \cdot (-1) + b \] \[b = - 0,6 \]
Likningen for tangenten blir da:
\[y= -0,2x - 0,6 \]
j)
For å finne eventuelle vendepunkter deriverer vi funksjonen to ganger, altså deriverer den deriverte og setter uttrykket lik null:
\[f ''(x) = ( \frac 25 x + \frac 15 )' = \frac 25 \]
Vi ser at den dobbelderiverte er en positiv konstant som ikke kan bli null. Funksjonen vender sin hule side oppover og har ingen vendepunkter.
Nå ble man ikke bedt om å tegne grafen til funksjonen, men vi har følgende informasjon:
Da kan man jo trekke en kurve gjennom å få noe som ligner på dette:
Grenseverdi
Grenseverdien til en funksjon er den verdien funksjonsuttrykket går mot når den variable går mot en spesiell verdi.
Vi bruker følgende notasjon:
$\lim\limits_{x \rightarrow a}f(x) =K$
Som leses "limes f av x når x går mot a er k", eller "grensen f beveger seg mot når x går mot a er k".
$\lim\limits_{x \to 3} f(x) = \lim\limits_{x \to 3} x+2 = 5$
lim er en forkortelse for limes som betyr grense på latin.
For å finne grenseverdien til et flerleddet uttrykk, summerer man grenseverdien til de enkelte leddene.
<math>\lim\limits_{x\to3} g(x) = \lim\limits_{x\to3}x^2+2x+1 = 9+6+1 = 16 </math>
Med grenseverdi mener vi den verdi en funksjon f(x) går mot når x går mot et tall, eller mot uendelig.
Når man har brøkuttrykk kan man tilsynelatende få null delt på null som et svar. Null i nevner gir ikke mening og må omarbeides.
Grenseverdien til en brøkfunksjon der utrykkene i både teller og nevner blir null, finner man ved å faktorisere teller og nevner og forkorte brøken. Eventuelt kan man bruke L’Hopitals regel.
Dersom telleren går mot null og nevneren går mot noe annet, er grenseverdien null.
Dersom nevneren går mot null og teller går mot noe annet har man en vertikal asymptote og ingen grenseverdi.
Vi forutsetter <math>\lim\limits_{x \rightarrow a}f(x) =K </math> og <math>\lim\limits_{x \rightarrow a}g(x) = L </math>
Generelle sammenhenger $\lim\limits_{x \rightarrow a}[f(x) \pm g(x) ] $ $ =\lim\limits_{x \rightarrow a}f(x) \pm \lim\limits_{x \rightarrow a}g(x) $
$= K \pm L $$ \lim\limits_{x \rightarrow a}[f(x) \cdot g(x) ] $ $=\lim\limits_{x \rightarrow a}f(x) \cdot \lim\limits_{x \rightarrow a}g(x) $
$= K \cdot L $<math>\lim\limits_{x \rightarrow a}\frac{f(x)}{g(x)}= \frac{\lim\limits_{x \rightarrow a}f(x)}{\lim\limits_{x \rightarrow a}g(x)}= \frac KL \quad \quad \quad L\ne 0 </math> <math>\lim\limits_{x \rightarrow a}\frac{1}{f(x)}= \frac{1}{K} \quad \quad \quad K \ne 0 </math> Spesielle sammenhenger <math>\lim\limits_{x \rightarrow 0} \frac{sin x}{x}= 1 </math> <math>\lim\limits_{x \rightarrow 0} \frac{1 - cos x}{x}= 0 </math> <math>\lim\limits_{x \rightarrow \infty}(1 + \frac 1n)^n = e </math> <math>\lim\limits_{x \rightarrow 0}(1 + n)^{\frac 1n} = e </math> For $ \quad a \geq 1 \quad $
gjelder$ \lim\limits_{x \rightarrow - \infty}a^x = 0 $
$\lim\limits_{x \rightarrow + \infty}a^x = + \infty $For $ \quad 0 \quad< \quad a \quad< \quad 1 \quad $
gjelder$ \lim\limits_{x \rightarrow - \infty}a^x = + \infty $
$\lim\limits_{x \rightarrow + \infty}a^x = 0 $
Ensidig grenseverdi
Dersom en funksjon ikke er definert for alle verdier av x, eller den gjør "hopp" i funksjonsverdien kan det være nødvendig å undersøke hva funksjonen går mot når x nærmer seg et tall fra en spesiell side.
<math>\lim\limits_{x \rightarrow a^+}f(x) = K </math>
Uttrykket betyr at f(x) går mot K når x går mot a fra høyre.
<math>\lim\limits_{x \rightarrow a^-}f(x) = R </math>
Uttrykket betyr at f(x) går mot R når x går mot a fra venstre.
L'Hopitals regel
Regelen brukes til å finne grenseverdien av ubestemte uttrykk som <math> \frac 00 </math> eller <math> \frac{\infty}{\infty} </math> .
Regelen sier at dersom grensen
\[ \lim_{x \rightarrow a}\frac{f(x)}{g(x)} \]
eksisterer
så er det lik grensen
\[ \lim_{x \rightarrow a}\frac{f'(x)}{g'(x)} \]
der f '(x) er den deriverte til funksjonen f(x) og g '(x) er den deriverte til funksjonen g(x).
Eksempel 24:
<math> \lim_{x \rightarrow 1}\frac{ln x}{x - 1} </math>
her går både teller og nevner mot null. Vi deriverer i henhold til L'Hopitals regel:
<math> \lim_{x \rightarrow 1}\frac{ \frac 1x}{1} = 1 </math>
Av og til kan det være nødvendig å benytte regelen flere ganger for å komme fram til en løsning. Forutsetter at grensene eksisterer.
Kontinuitet
Dersom grafen til en funksjon er sammenhengende er funksjonene kontinuerlig.
Gitt en funksjon f og et tall k som er med i definisjonsmengden til f. Dersom $\lim\limits_{x \to k}f(x)= f(a)$, da er f kontinuerlig for x = k.
hvilket betyr at
1.f (a) eksisterer, f er definert i a
2.lim f (x) når x går mot a eksisterer
3.verdiene i 1. og 2. er like
Deriverbarhet
Dersom en funksjon ikke er kontinuerlig for x = a, så er funksjonen heller ikke deriverbar for x = a.
Dersom en funksjon er deriverbar for x = a, så er den også kontinuerlig for x = a.
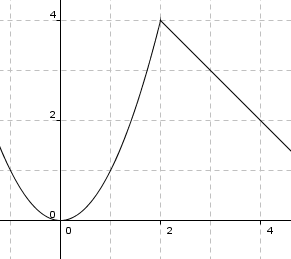
Kontinuerlig men ikke deriverbar for x = 2.
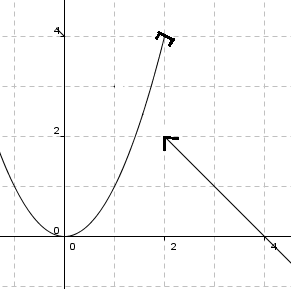
Ikke kontinuerlig eller deriverbar for x = 2
Omvendte funksjoner
Vi har en funksjon $f(x) = 0,25x$ Dersom vi setter inn x = 4 får vi funksjonsverdien 1. Vi har altså gått fra verdien 4 i definisjonsmengden til verdien 1 i verdimengden. En funksjon som tar oss tilbake fra 1 til 4 vil være en omvendt funksjon til f. Den ser slik ut: $f^{-1}(x) = 4x.$ Det som er definisjonsmengden til $f$ blir verdimengden til $f^{-1}$. $f$ og $f^{-1}$ er omvendte eller inverse funksjoner.
\[f^{-1}(f(x)) = x\]
- Funksjonens definisjonsmengde blir den inverse funksjonens verdimengde.
- Funksjonens verdimengde blir den inverse funksjonens definisjonsmengde.
Hvordan finne vi så den omvendte funksjonen? (bruker funksjonen over)
$f(x)= y$
$y = 0,25x$
$x= \frac{y}{0,25}$
$x = 4y$
$f^{-1} (y) = 4y$
$f^{-1} (x) = 4x$
Eksempel 25:
f og g er omvendte funksjoner. Man observere at de speiler hverandre om linjen y = x. Vi observerer også at x koordinaten til f blir y koordinaten til g, i tilsvarende punkt på respektive grafer. Det som er definisjonsmengden til den ene funksjonen er verdimengden til den andre.
Geogebra: man finner den omvendte funksjonen til f ved å skrive invers(f).
Eksempel 26:
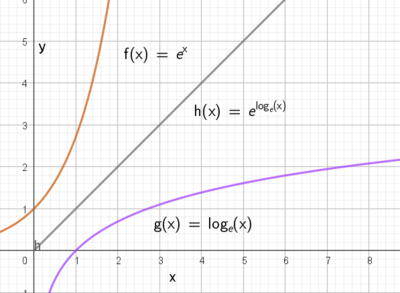
$f(x) = e^x$ og $g(x) = ln(x)$ er omvedte funksjoner. ( $ln(x) = log_e(x)$)
$h(x) = f(g(x)) = e^{ln(x)}= x $ (definisjon).
Setter vi f inn i g får vi $g(f(x))= ln(e^x)= x \cdot ln(e) = x \cdot 1 = x$.
$e^x$ og $\ln(x)$ er inverse funksjoner.
En- entydig
En funksjon er en- entydig dersom:
$x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2) $ for alle $x_1, x_2 \in \mathbb{D}_f$
En funksjon f har en omvendt funksjon hvis og bare hvis den er entydig.
Eksempel 27:
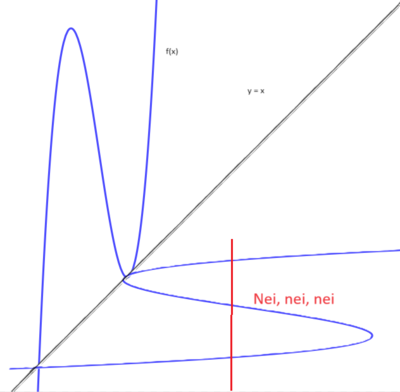
Vi ser at når f(x) speiles om linjen y=x får vi en kurve som ikke tilfredsstiller kravene til en funksjon, fordi en x verdi krysser kurven i mer enn ett sted. f(x) er ikke en- entydig i definisjonsområdet og har derfor ingen omvendt funksjon.
Den deriverte til inverse funksjoner
Dersom vi kjenner den omvendte funksjonen kan vi derivere den på vanlig måte. Dersom vi ikke kjenner den omvendte funksjonen kan vi allikevel finne den deriverte i et punkt, ved å gå veien om den deriverte til funksjonen.
g(x) er den omvendte funksjonen til f(x):
$g(f(x)) = x$
$(g(f(x)))' = x'\quad$ Bruker kjerneregel på venstre side
$g'(f(x)) f'(x) = 1$
$g'(f(x)) = \frac{1}{f'(x)}$
Det kan være umulig å finne g, men vi kan fortsatt finne den deriverte til g i et punkt.
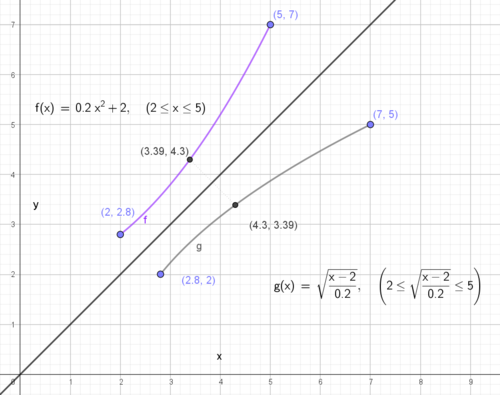
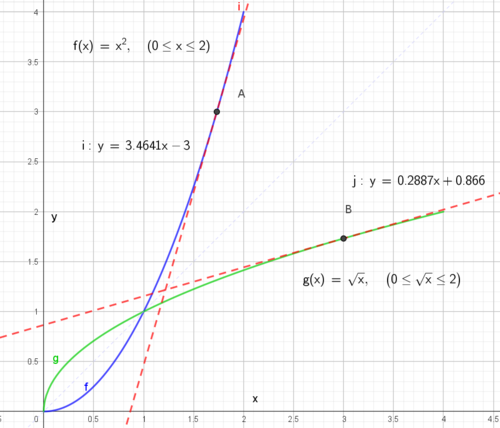
Eksempel 28:
Vi ser på funksjonen $f(x) = x^2, \quad x \in [0,2]$ Vi ønsker å finne den deriverte til den omvendte funksjonen g(x), for x=3. Da må vi først finne den x verdi som gir f(x)=3, husk at g sin definisjonsmengde er f sin verdimengde. f(x) = 3 gir x = 1,732. Vi bruker formelen for derivasjon av den omvendte funksjonen:
$g'(3) = \frac{1}{f'(1,732)}= \frac{1}{2 \cdot 1,732} = 0,288$.
Vi observerer at dette stemmer godt med grafene i figuren. Det er kanskje ikke så overraskende siden vi har symmetri om y=x, ikke bare for grafene til f og g, men også for korresponderende tangenter.
Absoluttverdifunksjoner
Absoluttverdi
Absoluttverdien er den positive verdien av uttrykket. Symbolet er vertikale "stolper". |3| = 3. Absoluttverdien av 3 er 3. |-3| = 3. Absoluttverdien av -3 er også 3. Man kan se på absoluttverdien som avstanden fra null, på tallinjen. Absoluttverdien sier noe om verdien, men ikke om retningen.
Absoluttverdi i den virkelige verden
Absoluttverdi er ikke en kunstig matematisk konstruksjon, men har en praktisk nytteverdi.
Mekanisk produksjon: Dersom du skal dreie en aksling til en maskin er det viktig at dimensjonen blir riktig. Dersom kunden ønsker at akslingen har en diameter på 100 mm. Kan det tenkes at du får denne beskrivelsen: |x-100|<0.1. Det betyr at akslingen kan ha et avvik på $\pm 0.1$ mm, altså må den være mellom 99,90 mm. og 100,10 mm.
Modellering Temperaturen i morgen blir mellom 12 og 16 grader: $|t-14|\leq 2$
Dette var bare to av mange praktiske anvendelser.
Noen viktige egenskaper:
$|a| \geq 0$
$|a| = 0 \Leftrightarrow a=0$
$|ab|= |a|\cdot|b|$
$|\frac ab | = \frac {|a|}{|b|}, \quad \quad b \neq 0$
$|-a| = |a|$
$|a| \leq b \Leftrightarrow \quad -b \leq a \leq b$
$|a| \geq b \Leftrightarrow \quad a \leq -b$ eller $a \geq b$
Eksempel 29:
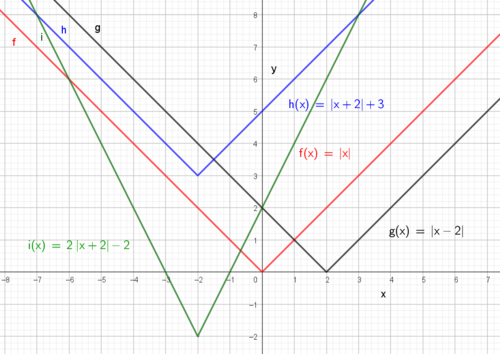
Fuksjonen absoluttverdien av x skrives slik:
\[ f(x)= |x| = \begin{cases}
\quad x,\quad x\geq 0 \\
\, \quad -x,\quad x < 0 \\
\end{cases} \]
Den røde grafen viser funksjonen. Vi observerer at den knekker i origo og danner 45 grader med x og y aksen. La oss se hvordan den kan påvirkes.
|x - a| gir knekkpunktet a enheter til høyre for origo (y-aksen). | x + b | skyver knekkpunktet b enheter til venstre for origo. Fortsatt ligger knekkpunktet på x- aksen.
|x| + a flytter knekkpunktet til a enheter over aksen, |x| - b flytter det b enheter under x - aksen.
Vi finner nullpunktene til i(x):
$i(x)=0$
$2|x+2|-2=0$
$|x+2|=1$
$x+2 = 1 \vee -(x+2)=1$
$x= -1 \vee x = -3$