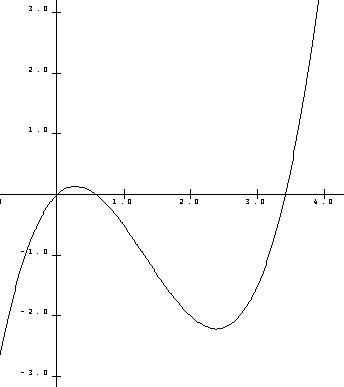Funksjonsdrøfting

Funksjonsdrøfting er analytiske undersøkelser av funksjonen og ender ofte opp med at vi skisserer (tegner) grafen i et koordinatsystem. I en tid med grafiske kalkulatorer og software for alle mulige analyser kan man jo spørre seg om nødvendigheten og viktigheten av å kunne gjøre dette "manuelt"? Svaret, etter vår mening, er at kalkulator og PC kan hjelpe deg til å få en økt forståelse og er glimrende verktøy, men kun en manuell gjennomgang viser om du har forstått emnet. Nedenfor følger en liste over ting du bør få klarhet i før du tegner grafen til funksjonen. Enkelte punkter kan det være vanskelig å få oversikten over, da går du videre til neste punkt. Vi kaller funksjonen f.

•Finn definisjonsmengden til f og finn eventuelle asymptoter.

•Finn eventuelle nullpunkter til f. f(x) = 0

•Finn punktet der grafen krysser Y aksen. f(0) = ?

•Finn <math>f'(x)</math>, finn eventuelle nullpunkter og drøft fortegnet til den deriverte.

•Finn <math>f(x)</math>, finn eventuelle nullpunkter og drøft fortegnet til den dobbelderiverte.

•Se etter mulig symmetri.

La oss se på et eksempel:

Gitt er funksjonen <math>f(x) = \frac 12 x^3 - 2x^2 + x</math>

Finn eventuelle ekstremalpunkter og tegn grafen i et koordinatsystem.

Funksjonen er definert for alle x element i R. Dersom du har med rasjonale funksjoner å gjøre må du sjekke for hvilke x verdier nevneren er lik null. Funksjonen vil ikke være definert for x verdier som gir null i nevner. Du må også sjekke for horisontale og vertikale asymptoter. Funksjonen i vårt eksempel har ingen asymptoter. Ofte er det slik at funksjonens definisjonsmengde er gitt.

For å finne funksjonens nullpunkter (der grafen krysser x aksen) må vi sette funksjonsuttrykket lik null, f(x) = 0. I vårt tilfelle har vi med en tredjegradsligning å gjøre. Disse kan være vanskelige å løse, men i dette tilfelle ser vi at det er mulig å faktorisere.

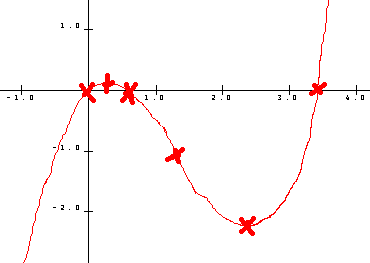
Hvilket gir x =0 som en løsning. Vi finner røttene av den andre faktoren ved å løse andregradslikningen 1/2X2 - 2X + 1 = 0. Løsningen er 0,59 og 3,41. Det betyr at grafen krysser x aksen tre steder, i punktene (0,0), (0,59, 0) og (3,41, 0).

f(0)= 0, det betyr at grafen krysser y aksen o punktet (0,0).

Vi deriverer funksjonen og får:

For å finne eventuelle nullpunkter setter vi f ' (x) = 0 og får en andregradslikning med følgende løsninger: 0,3 og 2,4.

Det betyr at grafen har ekstremalverdier for x = 0,3 og for x = 2,4. Vi kjenner x verdiene. for å finne y verdiene setter vi inn f(0,3) og f(2,4) og får f(0,3)= 0,13 og f(2,4) = 2,2. Det betyr at punktene (0,3 , 0,13) og (2,4, 2,2) er ekstremalpunkter. Vi må undersøke den deriverte for å finne ut hva som skjer mellom disse punktene. Vi lager et fortegnskjema.

f '(0) = 1

f '(1) = -1,5

f '(3) = 2,5

Det betyr at den deriverte er voksende (positiv) fra minus uendelig til 0,3. Fra 0,3 til 2,4 er den deriverte avtagende (negativ). Og fra 2,4 til pluss uendelig er den deriverte voksende. Vi får følgende skjema:

Vi begynner å kjenne funksjonen ganske godt nå, men det er et viktig punkt vi må finne. Et eller annet sted mellom x =0,3 og x =2,4 har funksjonen et vendepunkt. Vi finner dette ved å finne den dobbelderiverte og sette den lik null.

Vi finner hva f(x) er når x = 4/3:

f(4/3) = -1,04

Vi har nå følgende punkter og kan tegne grafen:

Dersom du får litt trening (og hjelp av en PC) kan det se slik ut:

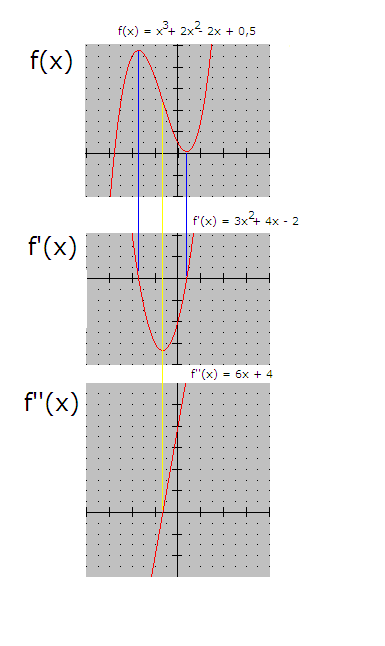
Funksjonsutrykket f(x)

f(x) = 0 Løsningene av ligningen gir alle funksjonens nullpunkter (der grafen krysser x aksen).

Den deriverte f’(x)

f ’(x) = 0 Løsningen av ligningen gir x verdiene for maksimums- eller minimumspunkter til f, også kalt ekstremalpunkter. Dersom f’(x) er positiv vokser f(x). Er f’(x) negativ avtar f(x). Grafen til f’(x) viser vekstforløpet til f(x). For å avgjøre om et ekstremalpunkt er et toppunkt eller et bunnpunkt lager man et fortegnsskjema. For å få med alle funksjonens ekstremalpunkter må man også sjekke punkter der funksjonen ikke er deriverbar, som knekkpunkter og endepunkter.

Den dobbelderiverte f’’(x)

f’’(x) = 0 Løsningen av ligningen gir vendepunktet(ene) til f. Dersom den dobbelderiverte er en konstant har f ingen vendepunkter. Dersom den dobbelderiverte er negativ krummer grafen sin hule side nedover. Er den dobbelderiverte positiv vender grafen sin hule side oppover.
Eks. :