Løsning del 1 utrinn Vår 10
Oppgave 1
a)334 + 465 = 799
b) 854 - 328 = 526
c)<math> 4,3 \cdot 7 = 30,1</math>
d) 264 :4 = 66
Oppgave 2
a) <math>2,5t = 2,5 \cdot 60 min = 150 min</math>
b)<math>4,7mil = 4,7\cdot 10 km = 47km</math>
c)<math>2,3 liter = 2,3\cdot 10 desiliter = 23 desiliter</math>
d)6250 g = 6250 : 1000 kg = 6,250kg
Oppgave 3
a) <math>3^2 +2(5-4) = 9 + 2 = 11 </math>
a) <math>-1^2 \cdot 3(-2)^3 = -1 \cdot 3(-8) = 24 </math>
Oppgave 4
a) <math> \frac{8}{13} + \frac{4}{13} = \frac{8 + 4}{13} =\frac{12}{13} </math>
b) <math> \frac{5}{6} - \frac{2}{3} = \frac{5}{6} - \frac{4}{6}=\frac{1}{6} </math>
c) <math> \frac{7}{9} \cdot \frac{1}{2} = \frac{7 \cdot 1}{9 \cdot 2}=\frac{7}{18} </math>
d) <math> 6:\frac{3}{10} = 6 \cdot \frac{10}{3}=\frac{6 \cdot 10}{3} = 20 </math>
Oppgave 5
a)
<math>4x+7 = 47 \\4x=47-7 \\4x=40 \\\frac{4x}{4}= \frac {40}{4} \\x= 10</math>
b)
<math>\frac x2 =\frac x3 +1 \\6 \cdot \frac x2 = 6 \cdot \frac x3 + 6 \cdot 1 \\3x = 2x + 6 \\x=6</math>
Oppgave 6
Dette er det vi kaller overslagregning. Vi runder av til tall det er lett å regne med i hodet:
348 euro <math>\approx </math> 350 og kursen er 8,732 <math>\approx </math> 9,0
Vi får da 350<math>\cdot </math> 9. Det kan være problematisk å ta i hodet, men dersom vi setter 10 i stedet for 9 får vi 3500, så kan vi trekke fra 350 og får 3150 kr. Dette er mer enn svaralternativene. Vi rundet begge verdier oppover, derfor vil overslaget vi gjorde gi et større beløp enn det som er helt riktig. Altså er ca. 3000 kroner riktig svar.
Oppgave 7
Oppgave 8
Overflaten av en sylinder er
<math> \pi\cdot r^2 + \pi\cdot r^2 + 2\pi rh = 2\pi\cdot r^2 +2\pi rh =2 \cdot 3 \cdot (5cm)^2 + 2 \cdot 3 \cdot 5cm \cdot 10cm = 150cm^2 + 300cm^2 =450cm^2</math>
Overflaten er noe større enn dette i virkeligheten, siden vi avrundet pi til 3.
Oppgave 9
<math> x+y= 3 \\ 2x+3y=8 \\ x=3-y \\ 2x+3y=8</math>
Sette uttrykket for x fra første likning inn i den andre og får
<math>2(3-y)+3y=8\\6-2y+3y=8 \\y=2</math>
Setter så inn y=2 i den første likningen, for å finne x. Vi får da at x=3-2, dvs. x = 1 og y = 2.
Oppgave 10
Dersom et kart har målestokk 1:1000 betyr det at 1cm på kartet er 1000 cm i terrenget. Vi vet at Oslo Bergen er ca 300km = 300.000m = 30.000.000 cm. Vi målte ca 1,9 cm, det må bety at målestokken på kartet er en til femten millioner. 1:15.000.000.
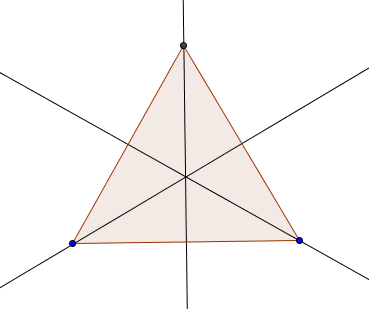
Oppgave 11
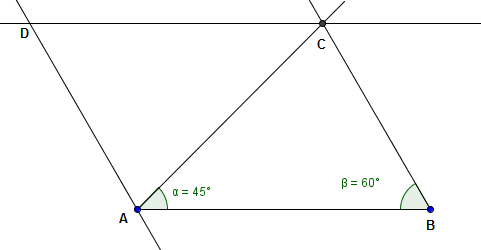
Bildet over er ingen konstruksjon, men en tegning av hvordan konstruksjonen blir seende ut.
Avsett linjestykke AB lik 7 cm
Konstruer en 45 graders vinkel i A, (halver en 90 graders vinkel)
Konstruer en 60 graders vinkel i B
Der linjene møtes ligger punktet C
For å konstruere parallellogrammet konstruerer du en linje gjennom C, parallell med AB. Avsett lengden AB fra C og mot venstre, og du har punktet D. Trekk linjen AD.
Oppgave 12
En rett linje har funksjonsuttrykk y = ax + b, der b forteller hvor grafen krysser y aksen og a forteller hvor mye grafen stiger. På figuren ser man en graf som krysser y aksen i -1 og stiger med 2 enheter. Man får y = 2x-1 som er det fjerde alternativet.
Oppgave 13
Ti prosent av 2990kr er 299kr. Du får 299 kr i rabatt.
Oppgave 14
a) 38 utfall
b) <math>\frac{19}{38} = \frac12 = 50 </math>%
Oppgave 15
Oppgave 16
Volum av eske:
<math>V= ghb= 20cm\cdot 15cm \cdot 10 cm = 3000cm^3</math>
Oppgave 17
Vi organiserer svarene i stigende rekkefølge:
1,1,1,1,1,2,2,3,3,5
a) Typetall er den observasjonen det er mest av, altså 1.
b) Median er det tallet som står i midten når tallene er organisert i stigende rekkefølge. Når observasjonsmengden er partall blir median gjennomsnittet av de to tallene i midten, i dette tilfelle 1,5.
c) Gjennomsnittet er summen av alle observasjoner delt på antallet observasjoner. I dette tilfelle 20 delt på 10 som er 2.
Oppgave 18
a) <math>A = \frac{gh}{2}= \frac{6m \cdot 8m}{2}= 24m^2 </math>
b) <math>x^2= (8m)^2+(6m)^2= 100m^2 \\ x= 10m</math>
En lengde er en positiv størrelse, derfor er x = - 10m ingen løsning på denne oppgaven.
Oppgave 19
Vi har at <math> v = \frac st \Rightarrow t = \frac sv </math>
Farten er <math>300000000 m/s = 3,0 \cdot 10^8 m/s</math>
Vi får da <math>t = \frac sv = \frac{3,84 \cdot 10^8m}{3,0 \cdot 10^8 m/s} = 1,3 s </math>
Svaret blir da ca. 1 sekund.
Oppgave 20
Han kommer til bussholdeplassen 07.38 + 00.05 = 07.43
Neste buss går 09.19.
Han må vente i 17 minutter til klokken er 08.00, så må han vente en time, fra 8 til 9. Til slutt må han vente i 19 minutter, fra 09.00 til 09.19.
Han venter altså i 00.17 + 01.00 + 0019 = 01.36 eller 1 time og 36 minutter.
Oppgave 21
a)
6a + 3b = 3(2a + b)
b)
<math>a^2+2ab+b^2 = (a+b)(a+b) = (a+b)^2</math>
Oppgave 22
Den lille kulen har radius r. Volumet blir da
<math>V = \frac{4 \pi r^3}{3}</math>
Den store kulen har en radius som er dobbelt så stor som den lille, altså 2r. Volumet av den store kula blir da
<math>V = \frac{4 \pi (2r)^3}{3} = \frac{4 \pi 8r^3}{3} = \frac{32 \pi r^3}{3} </math>
Når man deler volumet av den store kula på volumet av den lille kula får man at forholdet mellom volumene er 8.