Løsning del 1 utrinn Vår 15 eksempeloppgave
DEL EN
Oppgave 1
a) $987 + 589 = 1576$
b) $8643 - 4789 = 3854$
c) $345 \cdot 678 = 233 910$
d) $32:0.64 = 50$
Oppgave 2
a) $205 \text{min} = 3 \text{h} 25 \text{min}$
b) $8 000 \text{mg} = 0.008 \text{kg}$
c) $750 \text{mL} = 0.75\text{L}$
d) $1 \text{daa (dekar)} = 1000 m^2$
$11 500 m^2 = 11.5 \cdot 1000 m^2 = 11.5 \text{daa (dekar)}$
Oppgave 3
a) $\frac{3}{10} \cdot 15 = \frac{3 \cdot 15}{10} = \frac{45}{10} = \frac{9}{2} = 4 \frac12 $
b) $6:\frac{3}{4} = 6 \cdot \frac{4}{3} = \frac{6 \cdot 4}{3}= \frac{24}{3} = 8$
Oppgave 4
a) $1 + 2 \cdot (3-4) ^2 = 1 + 2 \cdot (-1)^2 = 3 $
b) $ -5 \cdot (-2 + 4) ^2 - \frac{2^3}{4} = -5 \cdot (2)^2 - 2= -22$
Oppgave 5
a)
$x + 3 = -3x +7$
$x + 3x+ 3 = 7$
$x + 3x = 7 - 3$
$4x = 4$
$x = 1$
b)
$\frac{x}{6} - \frac{2-x}{4} = \frac{x}{3} +1 \quad | \cdot 12 $
$2x - 3 \cdot (2-x) = 4x + 12 \\ 2x - 6 + 3x = 4x+12 $
$2x + 3x - 4x = 12 + 6 \\ x = 18$
Oppgave 6
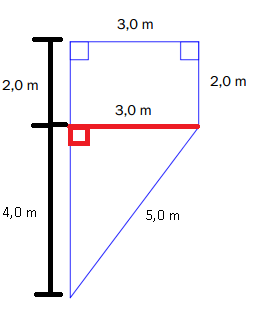
Deler opp figuren i et rektangel og en trekant. Trekanten er rettvinklet, og har to kateter med sider 3 m og 4 m. Kan derfor bruke pythagoras for å finne den ukjente siden.
$3.0^2 + 4.0^2 = x^2$
$9.0 + 16.0 = x^2$
$25.0 = x^2$
$5.0 = x$
$x = 5.0$
Hypotenusen er 5.0 m.
Finner så omkretsen: $ 6.0m + 3.0m + 2.0m + 5.0m = 16.0 m$
Hjelpetegning:
Oppgave 7
a) Én T-skjorte koster $100$ kroner. Det vil si at 3 T-skjorter normalt ville kostet $300$ kroner. Men ettersom jeg benytter meg av tilbudet ta tre, betal for to, så betaler jeg kun 200 kr. Avslaget jeg får er $300 - 200 = 100 kr$. Finner så hvor mange prosent 100 kr er av 300 kr.
${100 kr \over 300 kr} \approx 0.33 = 33\%$
Jeg får $33\%$ avslag.
b) Pondus har fått 5 flasker sjampo og bare betalt for 2 flasker sjampo. Pondus har altså fått $5-2=3$ flasker i avslag.
${3 \text{flasker} \over 5 \text{flasker}} = 0.6 = 60\%$
Pondus har fått $60\%$ avslag.
Oppgave 8
a) Hva er $86^o$ Fahrenheit i Celsius? Bruker formelen $C=\frac{5}{9} \cdot (F -32)$
$C= \frac{5}{9} \cdot (86^oF -32) = 30^oC$
$86^o$ Fahrenheit tilsvarer $30^o$ Celsius
b) $C=\frac{5}{9} \cdot (F -32)$
$\frac{9}{5} \cdot C= F -32$
$\frac{9}{5} \cdot C + 32 = F$
$F = \frac{9}{5} \cdot C + 32$
Oppgave 9
a)
$\frac{4x^2}{2x} = \frac{2 \cdot \bcancel{2} \cdot x \cdot \bcancel{x}}{\bcancel{2} \cdot \bcancel{x}} = 2x$
b)
$\frac{5x + 25}{x^2 -25} = \frac{5x + 5 \cdot 5}{x^2 -5^2} = \frac{5\bcancel{(x + 5)}}{(x-5)\bcancel{(x+5)}} = \frac{5}{x-5}$
Oppgave 10
A: Sannsynligheten for å få en femmer når man kaster en terning er $\frac{1}{6} = \frac{1\cdot 6}{6\cdot 6} = \frac{6}{36}$
B: Sannsynligheten for å få sum 6 når man kaster to terninger er $\frac{5}{36}$ (teller antall kombinasjoner på bildet som gir sum 6)
Ettersom $ \frac{6}{36} > \frac{5}{36}$ så er det korrekte svaret:
A er mest sannsynlig.
Oppgave 11
a)
Typetallshøyden for de 4 spillerne er den hyppigst forekommende verdien. Den verdien som forekommer flest ganger er 175 cm (to spillere). Dermed er typetallshøyden $175$cm
b)
Sorterer observasjonene: $175_{(1)} \;\; 175_{(2)} \;\; 185_{(3)} \;\; 189_{(4)}$
Finner antall observasjoner: N = 4
Finner midtpunktet: ${N + 1 \over 2} = {4 + 1 \over 2} = 2.5$
Fordi det er et partall antall observasjoner er medianen lik gjennomsnittet av de to verdiene som ligger på hver sin side av midtpunktet
Medianen er gjennomsnittet av verdiene nummer 2 og 3. ${175 + 185 \over 2 }= 180$
Medianhøyden for spillerne er 180 cm.
c)
Finner summen av observasjonsverdiene: $S=185+175+175+189=724$
Finner antall observasjoner: N=4
Gjennomsnittet er da: ${S \over N} = {724 \over 4} = 181$
Gjennomsnittshøyden for de 4 spillerne er 181 cm.
Oppgave 12
$\bigtriangleup ABC$ er formlik med $\bigtriangleup EBD$
Derfor er $\frac{BC}{AC} = \frac{BD}{DE}$
Finner den ukjente siden BC:
$\frac{BC}{4.0km} = \frac{4.5km}{3.0km}$
$BC = \frac{4.5km \cdot 4.0 km}{3.0km}$
$BC = \frac{4.5km \cdot 4.0 km}{3.0km} = 6 km$
Dermed vet vi at BC er 6 km.
Oppgave 13
Finner først hva 1 cm på kartet tilsvarer i virkeligheten. $\frac{2.5km}{5} = 0.5 km$
Regner så om 0.5 km til cm. $0.5 km = 0.5 \cdot 1000 m = 0.5 \cdot 1000 \cdot 100 cm = 50000cm$
Målestokken er derfor $1 : 50 000$
Oppgave 14
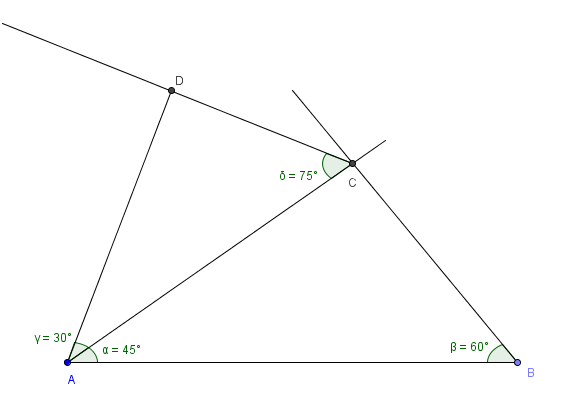
Avsett AB = 9 cm.
Konstruer en 45 graders vinkel i A (halver 90).
Konstruer en 60 graders vinkel i B.
Konstruer en 30 graders vinkel med toppunkt i A, høyre vinkelbein er AC (halver 60).
Konstruer en 75 graders vinkel med toppunkt i C (60 + 15), der linjene krysser hverandre ligger D.
Oppgave 15
a)
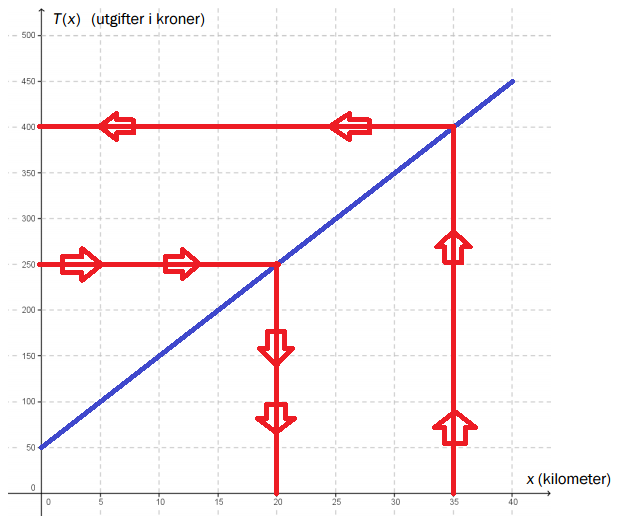
$T(x) =10x +50$
$T(0) =10 \cdot 0 +50 = 50$
Svaret betyr at det koster 50 kroner å starte en taxitur. Det koster altså 50 kroner å sette seg inn i taxien uten å kjøre noe sted.
$T(15) =10 \cdot 15 +50 = 150 + 50 = 200$
Svaret betyr at det koster 200 kroner å kjøre 15 km i taxi.
b)
For 250 kr kan vi kjøre 20 km.
Å kjøre 35 km koster 400 kr.
Oppgave 16
Område 2 og 3:
$A = \pi r^2$
De små sirklene har tilsammen arealet $ 2 \pi r^2$
Areal av stor sirkel minus de to små: $A= \pi (2r)^2 - 2 \pi r^2 = 4 \pi r^2-2 \pi r^2 = 2\pi r^2$
Siden område 1 og 4 er like store, er hvert av områdenes areal $ A= \pi r^2$
Alle områdene er altså like store.