Løsning del 1 utrinn Vår 18
Vår 2018
DEL EN
Oppgave 1
a)
500g $\cdot$ 6 = 3000g = 3 kg
b)
3 km på 20 minutter. 20 minutter er $ \frac 13$ time: $v = \frac st = \frac{3km}{\frac13 time} = 3 km \cdot \frac 31 time= 9 $ km /t
Gjennomsnittsfarten er 9 km/h.
Oppgave 2
a)
$2^3 - 2 = 8-2 =6$
b)
$\frac{2^2\cdot 2^4}{2+2} = \frac{4 \cdot 16}{4} = 16$
Oppgave 3
$ 7,5 \quad \sqrt{64}=8 \quad 3\pi > 9,4 \quad \frac{36}{4} = 9$
Den laveste verdien er 7,5
Oppgave 4
a)
$1-( \frac 15 + \frac 14) = 1- (\frac{4}{20} + \frac{5}{20}) = 1- \frac{9}{20} = \frac{11}{20} = \frac{55}{100}$
Altså 55%
b)
$40 \cdot \frac 15 = 8 $, altså 8 strategispill.
Oppgave 5
For fire personer finnes det 4! mulige rekkefølger:
$4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24$
Oppgave 6
a)
Sannsynligheten for gul blir antall gunstige delt på antall mulige, altså: P ( gul) = $ \frac{23}{102}$.
b)
Sannsynligheten for ikke å trekke sort kan skrives slik: $P( \overline{sort})$
Tar de Nonstoppene som ikke er sorte og deler på antall mulige:
$P( \overline{sort}) = \frac{82}{102} = \frac{41}{51}$
Oppgave 7
$7500 000 000= 7 ,5\cdot 10^9 $
Oppgave 8
$48,50 : 13,90 = \\485 : 139 \approx 3,5$
Hun kjøper ca 3,5 hg smågodt.
Oppgave 9
$4y = 180^{\circ} \\ y= 45^{\circ}$
Vinkel y er 45 grader.
Oppgave 10
a)
3(a+2) -2a = 3a+ 6 -2a = a + 6
b)
$ \frac{a^2+a}{2a+2} = \frac{a(a+1)}{2(a+1)} = \frac a2$
Oppgave 11
a)
$6x+3 = 17 - x \\ 7x = 14 \\ x = 2$
b)
$x - \frac{x}{3} = \frac{x+1}{2} \quad | \cdot 6 \\ 6x -2x = 3(x+1) \\ 4x = 3x+3 \\ x = 3 $
Oppgave 12
Espresso og melk i forholdet 1: 3, altså fire deler til sammen. Dersom blandingen er 6dl utgjør en del $\frac 64$ = 1,5 dl. Tre deler blir da 4,5 dl.
Oppgave 13
a)
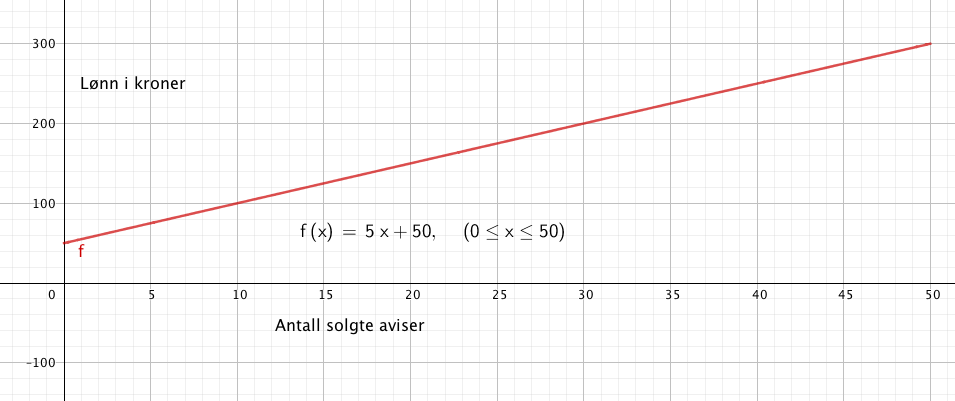
Fastlønn på kr. 50 og 5 kroner per solgt avis gir en lønn y på:
y = 5x + 50 , der x er antall solgte aviser.
b)
Grafen viser lønn som funksjon av antall solgte aviser i intervallet null til femti aviser.
Oppgave 14
Vinkelsummen i en trekant er 180 grader. En femkant kan deles i tre trekanter så vinkelsummen blir tre ganger så stor, altså $540^{ \circ} $.
Oppgave 15
Sirkel A, radius x: $O_A = 2 \pi r = 2 \pi x$
Sirkel B, radius 2x: $O_B = 2 \pi r = 2 \pi (2x) = 4 \pi x$
Omkretsen av sirkel B er dobbelt så lang som omkretsen av sirkel A.
Oppgave 16
Vi kan løse denne oppgaven på to måter, addisjonsmetoden og innsettingsmetoden. Uavhengig av metode, setter vi opp likningssystemet først.
Pris ball : x
Pris bukse: y
<math> \left[ \begin{align*}2x+y=2100 \\ 3x + y = 3000 \end{align*}\right] </math>
Addisjonsmetoden:
Ganger den første likningen med minus en og legger likningene sammen.
<math> \left[ \begin{align*}-2x-y=-2100 \\ 3x + y = 3000 \end{align*}\right] </math>
x= 900
Setter inn i likningen og finner at y= 300.
Buksen koster 300 kroner og ballen koster 900 kroner.
Innsettingsmetoden:
Løser for y i første likning:
<math> \left[ \begin{align*}y=2100 -2x \\ 3x + y = 3000 \end{align*}\right] </math>
Setter så inn for y i andre likning:
<math> \left[ \begin{align*}y=2100-2x \\ 3x + (2100-2x) = 3000 \end{align*}\right] </math>
<math> \left[ \begin{align*}y=2100-2x \\ x = 3000 - 2100 \end{align*}\right] </math>
x = 900.
Setter inn i første likning og finner at y=300.
Buksen koster 300 kroner og ballen koster 900 kroner.
Oppgave 17
a)
Tre til fire timer: 25% $= \frac{25}{100} = \frac 14$
b)
30% av 63600:
$\frac{30 \cdot 63600}{100} =30 \cdot 636 = 19080$
19080 personer bruker mere enn fire timer i snitt foran en skjerm.
Oppgave 18
a)
Det horisontale kateter har lengden 10m - 4m - 2m = 4m, og det vertikale har lengden 3m.
Pytagoras: $x^2 = (4m)^2 + (3m)^2 = 25m^2 \\ x = \sqrt{25m^2} = 5m$
Lengden av x er 5 meter.
b)
Omkrets av sammensatt figur, begynner øverst i trekanten og går mot klokka:
O = 5,0 m + 10,0 m +5,0 m + 4,0 m + 3,0 m + 2,0 m + 5,0 m = 34,0 m
c)
Deler opp den sammensatte figuren i en trekant og to rektangler:
$A = \frac{3m \cdot 4m}{2} + 10m \cdot 2 m + 4m \cdot 3 m \\ A = 6m^2 + 20m^2 + 12m^2 \\ A = 38m^2$
Oppgave 19
Sylinder: $V_{sylinder} = \pi r^2h =\pi r^2 (2r)= 2 \pi r^3$
Kule: $V_{kule} = \frac 43 \pi r^3$
Kjegle: $V_{kjegle} = \frac{\pi r^2h}{3} = \frac{\pi r^2 (2r)}{3} = \frac 23 \pi r^3$
$V_{kule} + V_{kjegle} = \frac 43 \pi r^3 + \frac 23 \pi r^3 = \frac 63 \pi r^3 =2 \pi r^3= V_{sylinder}$