Løsning del 2 utrinn Vår 11
Oppgave 1
a)
Pris i 2010: <math>26990kr \cdot 1,12 = 30229kr</math>
b)
<math>v = \frac st \Rightarrow t = \frac sv = \frac{10km}{30 km/t} = \frac 13 time = 20 minutter.</math>
C)
600km = 60 mil, og den bruker 0,2 l/mil:
<math> 60mil \cdot 0,2 l/mil = 12 liter </math>
Oppgave 2
a)
Når man skal sammenligne størrelsen på brøker er det lettest om gjør om til felles nevner. I dette tilfellet er det lurt å gjøre om til en brøk med nevner lik 32:
<math> \frac 38 = \frac {12}{32}, \quad \frac {15}{32},\quad \frac {1}{2}=\frac {16}{32}, \quad \frac {19}{32},\quad \frac {11}{16}= \frac {22}{32}, \quad \frac {3}{4}= \frac {24}{32} </math>
b)
Her må man huske at diameter er to ganger radius:
<math> V= \pi r^2h = 3,14 \cdot (2,6cm)^2 \cdot 5,78cm = 122,75cm^2</math>
c)
Maksimum radius: <math> V= \pi r^2h \Rightarrow r = \sqrt{\frac {V}{\pi h} } =\sqrt{\frac {125,0 cm^3}{3,14 \cdot 5,78 cm} } = 2,6247cm </math>
Maksimum diameter blir da 2r som er 5,25cm eller 52,5 mm
Oppgave 3
Oppgave 4
a)
b)
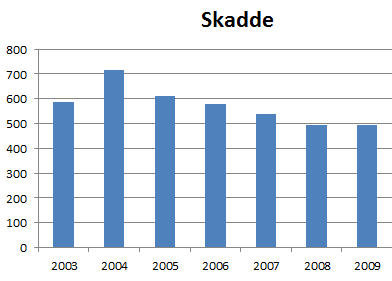
Gjennomsnitt:
<math>Snitt = \frac{585 + 715 + 613 + 577 + 537 + 494 + 494}{7} = 574</math>
Antall skadde var i gjennomsnitt 574 personer per år.
Oppgave 5
a)
Leser fra graf: Peder var i Ås fra 18:15 til 19:00, dvs. 45 minutter.
b)
Leser av graf: Køen begynte 30km fra Sarpsborg.
c)
Turen tok 1 time og 15 minutter som er 1,25 timer. Strekningen var 60km.
<math> v= \frac st \Rightarrow v = \frac{60km}{1,25t}= 48 km/t</math>
Oppgave 6
a)
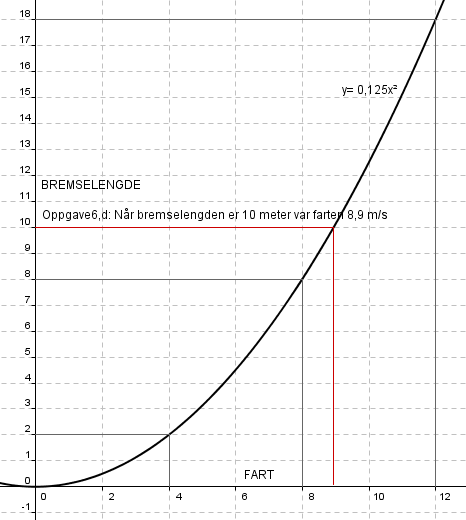
Fart = 8,0 m/s gir bremselengde 2 ganger 4 meter, dvs. 8m.
Fart = 12,0 m/s gir bremselengde 2 ganger 9 meter, dvs. 18m.
b)
<math>y = k \cdot x^2 \Rightarrow k = \frac{y}{x^2}</math>
Setter inn x = 4,0 og y = 2,0 og får:
<math>k = \frac{2,0}{4,0^2} = \frac {2}{18} = \frac 18 = 0,125</math>
c)
d) Se figur i c for grafisk løsning. Ved regning:
<math>y = k \cdot x^2 \Rightarrow 10,0 = 0,125 \cdot x^2 \Rightarrow x = \sqrt{\frac{10}{0,125}}=8,9</math>
Farten må ha vært 8,9 m/s når bremselengden er 10 meter.
Oppgave 7
a)
Areal: <math>A = (230m)^2 = 52900m^2</math>
Omkrets: <math>O = 4 \cdot 230m = 920m</math>
b)
Formlike trekanter:
<math>\frac {2}{7,5} = \frac{h}{546} \Rightarrow h = 145,6</math>
c)
Volum av pyramide:
<math>V = \frac 13Gh = \frac13 \cdot 52900m^2 \cdot 145,6m = 2567387,7 m^3</math>
Volumet er ca 2,57 milioner kubikkmeter.
d)
Bruker først Pytagoras for å finne avstanden fra toppen av pyramiden og ned til midten av en side.
<math>s = \sqrt{(115,0m)^2 + (145,6m)^2} = 185,5m</math>
Overflaten består av åtte rettvinklede trekanter med grunnlinje 115,0m og høyde 185,5m:
<math>O = 4 \cdot 115,0m \cdot 185,5m = 85330m^2</math>
Oppgave 8
Her burde det strengt tatt være nok å henvise til Thales' setning som jo er gitt i oppgaven, men dersom man ønsker å Vise (forklare) det kan man gjøre slik:
SB og SC har begge lengden r. Trekanten SBC er derfor likebeint.
Vinkel CBS er lik vinkel SCB, begge er 50 grader.
Vinkel BSC blir da 80 grader, som en følge av det blir vinkel CSA 100 grader.
Trekanten ASC er likebeint fordi AS = SC = r, da er vinkel SAC lik vinkel ACS, dvs. 40 grader.
Vinkel C er summen av vinkel SCB og ACS, dvs. 50 grader og 40 grader, tilsammen 90 grader.
Oppgave 9
Trekanten ABC er formlik med trekanten CDE.
<math> \frac{x}{x+30} = \frac {45}{50} \Rightarrow x =270</math>
Skipet er 270 meter fra land.