Løsning del 2 utrinn Vår 13
Oppgave 1
480kr + 145kr + 95kr<Math>\cdot</Math>4 + 950 kr = 1955kr
Hun betaler 25%: 1955kr <Math>\cdot</Math> 0,25 = 489kr.
Oppgave 2
a)
Hun kan velge på <Math>11 \cdot 10 \cdot 8 = 880</Math> måter.
b)
Sannsynligheten for at hun både velger riktig børste og riktig tråd er <Math> \frac{1}{11} \cdot \frac{1}{8} = \frac{1}{88}</Math>
Oppgave 3
Blandet i forholdet 1:3 gir det 1200ml ferdig blanding. Hun bruker 80ml daglig.
1200 : 80 = 15, dvs. en flaske varer i femten dager.
Oppgave 4
<Math>V= \frac{\pi \cdot h}{3} (R^2 + r \cdot R + r^2) = \frac{8\pi}{3} (3,3^2+2,3 \cdot 3,3 + 2,3^2) cm^3 = 199,1 cm^3 \approx 2dl</Math>
Oppgave 5
a)
b)
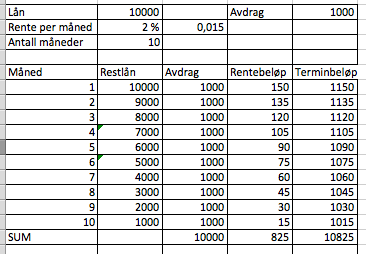
Rødt markerer rente og blått avdrag.
c)
Hun kan spare 1100 kr - 825kr = 275 kr ved å velge dette lånet.
Oppgave 6
a)
<Math>h(x) = -0,05x^2+x+2 \\ h(10) = -0,05 \cdot 100 + 10 + 2 = -5 +10 + 2 =7</Math> ,
dvs. syv meter over bakken etter ti meter fra Rampe 1.
b)
Brukte kommandoen Funksjon[<Funksjon>,<Start>,<Slutt>] for å tegne grafen for x-verdier mellom 0 og 20.
c)
Motorsykkelen er 4 meter over bakken to steder, etter 2,25 meter på vei opp, og etter 17,75 meter på vei ned, målt fra Rampe 1. Se bilde i b).
Oppgave 7
a)
Trekant AOC er likebeint der siden AO = OC = 5,0 cm, fordi vinkel A og C begge er 45 grader, kan også se at OC = 5,0 cm ved å legge merke til at den er radien i sirkelen. Trekanten er rettvinklet og man kan bruke Pytagoras:
<Math>(AC)^2 = (5cm)^2 + (5cm)^2 \\ AC = \sqrt{50} cm</Math>
b)
Arealet til halvsirkelen ABC: <Math>A = \frac{\pi r^2}{2} = \frac{25\pi cm^2}{2} = 12,5 \pi cm^2 =39,25 cm^2</Math>
Oppgave 8
Lengden av den blå linjen:
<Math>O = AEC_{sirk} + CB_{sirk} + BH + HG + GA \\ O = 2 \pi \frac{\sqrt{50}}{4} cm + \frac{2 \pi \cdot 5}{4} cm +10cm +10cm +10cm \\ O = ( \frac{\sqrt{50}\pi}2 + \frac 52 \pi +30)cm \\ O = 48,96 cm</Math>
Oppgave 9
a)
Areal av halvsirkel AEC:
$\frac 12 \pi \cdot (\frac{\sqrt{50}}{2})^2 = \pi \frac{50}{8} = 19,625$
b)
Areal av halvsirkel ACB:
$\frac 12 \pi \cdot 5^2 = \pi \frac{25}{2}$
Ser først på forholdet mellom den lille og den store halvsirkelen
$\frac{\text{AEC}}{\text{ACB}} = \frac{\pi \frac{50}{8}}{ \pi \frac{25}{2}} = \frac 12 $
Areal av kvadrat AFBC:
$\sqrt{50}^2 = 50$
Areal av kvadrat AGHB:
$10^2 = 100$
Forholdet mellom det lille kvadratet og det store,
$\frac{50}{100} = \frac 12$
er likt forholdet mellom halvsirklene.
Oppgave 10
<Math>(AC)^2 = r^2+r^2 \\ (AC)^2 = 2r^2 \\ AC = \sqrt2r </Math>
AD er radius i halvsirkelen AEC : AD = r' = <Math>\frac12 \sqrt2r</Math>
Areal av trekanten AOC : <Math>A = \frac{Gh}{2} = \frac{r \cdot r}{2} = \frac{r^2}2</Math>
Areal av halvsirkelen AEC: <math>A = \frac{\pi (\frac{\sqrt2r}{2})^2}{2} = \frac{\pi r^2}{4}</math>
Areal av kvartsirkelen AOC: <math> A= \frac{\pi r^2}{4}</math>
Arealet av halvmånen blir : A = halvsirkel AEC - ( kvartsirkel AOC - trekant AOC)
<math> A = \frac{\pi r^2}{4} - \frac{\pi r^2}{4} + \frac{r^2}2 = \frac{r^2}2 </math>