Parabel
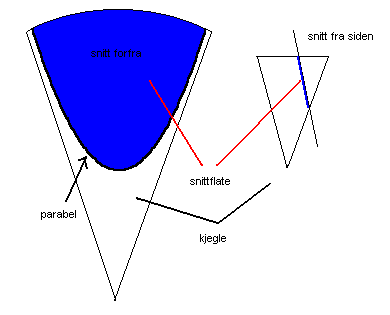
Parabelen tilhører familien av kurver som vi kaller for kjeglesnitt. Vi kan tenke oss at vi snitter en kjegle på følgende måte:
Snittflatens kant har form som en parabel.
En andregradsfunksjon kan generelt skrives som:
<math>f(x) = ax^2 + bx + c</math>
Grafen til en andregradsfunksjon er en parabel.
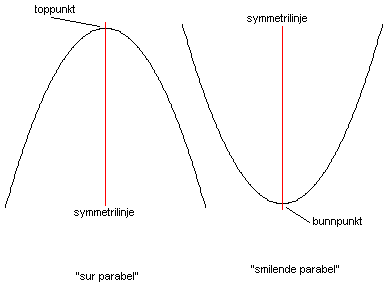
Dersom a er større enn null vender parabelen sin hule side oppover (den "smiler").
Dersom a er mindre enn null vender parabelen sin hule side nedover (den er "sur").
En parabel er symmetrisk om en linje som går gjennom toppunktet eller bunnpunktet.
Symmetrilinjen er gitt ved:
<math>x= \frac{-b}{2a} </math>
Der a og b er konstantene fra andregradsfunksjonen.
LITT MER OM PARABELEN
Geometrisk sted
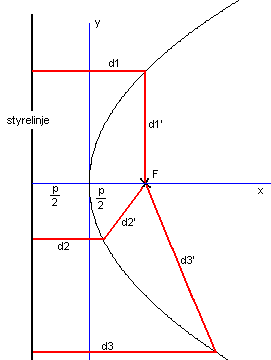
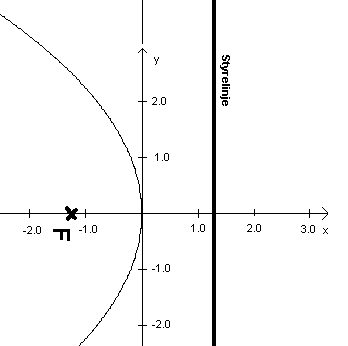
Geometrisk er en parabel mengden av alle punkter som ligger like langt fra en gitt linje og et gitt punkt. I matematisk litteratur fremstilles ofte parabelen med toppunktet enten til høyre eller til venstre. Om man tegner en vertikal styrelinje og et vilkårlig punkt F et sted i planet, men ikke på styrelinjen, kan det se slik ut:
Punktet F kalles for brennpunkt (Focal point på engelsk). Over ser vi at toppunktet er lagt i origo og at avstanden fra styrelinjen til toppunktet er lik den fra toppunktet til F, <math> \frac p2</math>. Et vilkårlig punkt på parabelen kan da uttrykkes ved:
avstand fra styrelinje = avstand fra brennpunkt
<math> \frac p2 + x = \sqrt{(x- \frac p2)^2 + y^2}</math>
som ordnet gir
<math> y^2 = 2px</math>
(Dersom du synes det er forvirrende med disse "liggende" parablene kan du bytte x og y og du får en "blid" eller "sur" parabel, avhengig om F ligger over styrelinja eller ikke.)
Et hvert punkt på parabelen vil ha lik avstand til styrelinjen og til punktet F. Det betyr at:
d1 = d1'
d2 = d2'
d3 = d3'
og så videre.
Eksentrisiteten til et kjeglesnitt er gitt som det konstante forholdet:
Avstand til brennpunkt delt på avstand til styrelinje.
Alle parabler har eksentrisitet 1.
Fra figuren ser vi at:
<math> \frac {d1'}{d1} = \frac {d2'}{d2} = \frac {d3'}{d3} = 1</math>
EKSEMPEL
La oss ta utgangspunkt i funksjonen
<math>f(x) = -0,2x^2</math>
Vi bytter f (x) med y og får
<math>y = -0,2x^2</math>
som gir:
<math>x^2 = -5y</math>
Skriver vi det på formen til likning (1) finner vi p:
<math>x^2 = 2(- \frac 52)y</math>
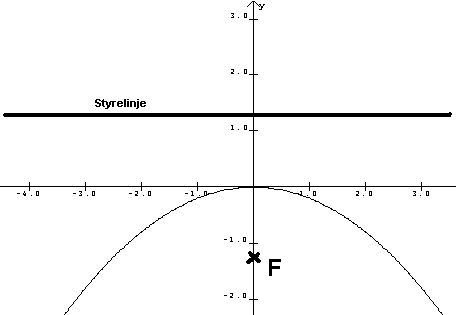
<math> \frac p2</math> er altså <math> \frac{-5}{4}</math> hvilket betyr at koordinatene til F er <math>(0, \frac{-5}{4})</math> som betyr at parabelen har sin åpning nedover.
Styrelinjen er parallell med x aksen og går gjennom punktet <math>y = \frac 54</math>.
Dersom vi bytter om x og y slik man antydet over får man:
<math>y^2 = -5x \\ y^2 = 2(- \frac 52)x</math>
Som gir en figur som uttrykke det samme i forhold til parabelen:
Så langt har parablene hatt toppunktet i origo.
En mer generell sammenheng finner vi om parabelen har toppunktet i et vilkårlig punkt, P(h,k)
Da gjelder følgende sammenheng:
<math> (y - k)^2 = 2p(x - h)</math>
(finnes ved samme resonement som over, bare at toppunktet nå ikke ligger i origo)
Eksempel.
Vi undersøker grafen til ligningen: <math>4y^2 - 8x - 12y + 1 = 0</math>
<math>4y^2 - 8x - 12y + 1 = 0 \\ 4y^2 -12y = 8x - 1 \\y^2 -3y = 2x - \frac 14 \\ y^2 -3y + ( \frac 32)^2 =2x +( \frac 32)^2 - \frac 14 \\ (y- \frac 32)^2 = 2 \cdot 1 \cdot (x+1) </math>
Vi ser at p =1, h = -1 og k =3/2. Det gir F(-1/2,3/2), Toppunkt i P(-1,3/2), symmetrilinje for y = 3/2 og styringslinje for x = -2.
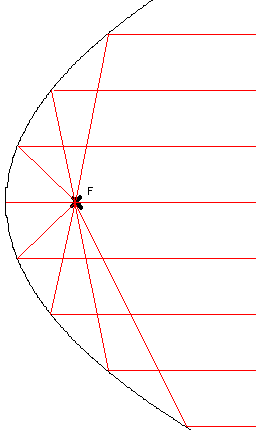
Refleksjonsegenskaper
Parabelen har spesielle refleksjonsegenskaper. alle stråler som kommer inn parallelt med symmetrilinjen og treffer parabelen reflekteres gjennom brennpunktet. Dette gir grunnlag for parabolantenner, solovner, solkraftverk, speillinser og mye mer.