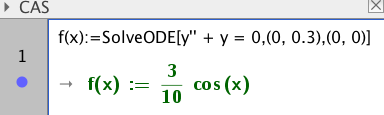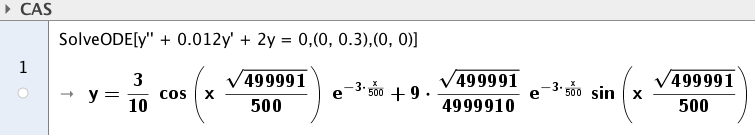Praktiske problemer der differensiallikninger er løsningen
Svingninger
Frie svingninger uten dempning
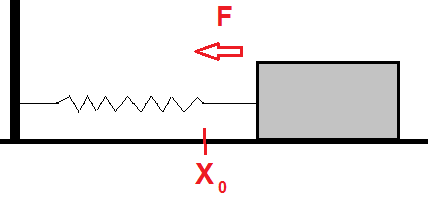
En kloss ligger på et friksjonsfritt underlag. Klossen er festet til en fjær som er fastspent i veggen slik figuren viser. Likevektspunktet er $x_0$. Utslaget fra likevektspunktet kalles x(t).
Newtons andre lov sier at summen av kreftene som virker på klossen er lik masse multiplisert med akselerasjon.
$\sum F = ma$
Hooks lov sier at:
$ F = kx $, k er fjærkonstanten. Siden kraften er proporsjonal med utslaget og virker hele tiden mot likevektspunktet, setter vi F = -kx
Vi får:
$m\frac{d^2x}{dt^2} = -kx $ som gir $\frac{d^2x}{dt^2} + \frac{k}{m}{x} = 0 $ Ved å innføre $\omega =\sqrt{\frac{k}{m}}$ får vi $ \frac{d^2x}{dt^2} + \omega^2x = 0 $
som er identisk med
$ x' ' + \omega^2x = 0 $
Her finner du hvordan disse likningene løses:
En kloss med masse 2,5 kg. ligger på en friksjonsfri overflate og er festet til en forankret fjær. Fjæren strekkes 0,5 meter med en kraft 1,25 Newton.
Klossen trekkes ut 0,3 meter mot høyre, fra likevektspunktet, der den slippes. Beskriv bevegelsen.
Løsning:
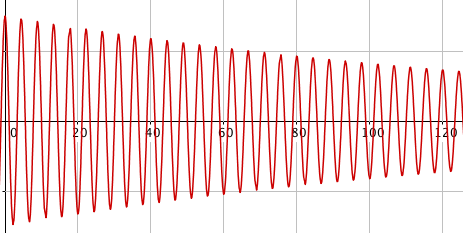
Vi ser bort fra friksjonen og har harmoniske svingninger.
$ x' ' + \omega^2x = 0 $
$ r^2 +\omega ^2=0 $
$ r^2 = -\omega^2 $
$ r = \pm \sqrt {- \omega^2} $
$ r = \pm \omega i $
Det gir oss følgende generelle løsning:
$y(t)= C_1 sin \omega t + C_2 cos \omega t$
For å finne den spesielle løsningen må vi bruke de opplysningene vi har:
- Fjærkonstanten k: $k = \frac Fx = \frac{1,25N}{0,5m} = 2,5$ N/m
- Ved tiden t=0 er y = 0,3; y(0)= 0,3
- I ytterstillingene er farten null, dvs $y'(0)= 0$
- Ved likevekt er kraften, og derved akselerasjonen null: $y' ' (0) = 0$
- $\omega = \sqrt {\frac{2,5}{2,5}} = 1$
Vi har $y(t) = C_1 sin t + C_2 cos t$ og deriver og dobbeltderiverer for å kunne bruke initialbetingelsene til å finne den spesielle likningen.
$y'(t)= C_1cos t - C_2sin t $ $ y' '(t) = -C_1 sin t - C_2 cos t$
$y(0) = 0,3 S S y(0)=C_1sin(0) + C_2cos(0)$
$ C_2=0,3 $ $ y'(0)=0 $ $ 0= C_1cos(0) -C_2sin(0) $ $ C_1=0 $
Funksjonen blir da: $y(t) = 0,3 cos(t)$
DIGITALT:
Frie svingninger med dempning
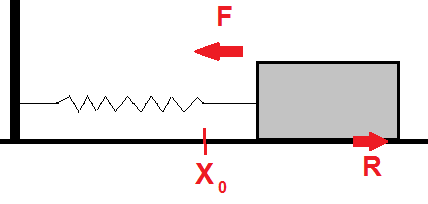
En kloss ligger på et underlag med friksjon. Klossen er festet til en fjær som er fastspent i veggen slik figuren viser. Likevektspunktet er <math>x_0</math>. Utslaget fra likevektspunktet kalles x(t).
Man antar at friksjonen R er proporsjonal med farten v og virker mot bevegelsen. v er x' og R = rx'
<math>m\frac{d^2x}{dt^2} = -rv - kx \Leftrightarrow m\frac{d^2x}{dt^2}+ r \frac{dx}{dt} + kx =0</math>
$ mx' ' + rx' + kx = 0 $ eller
$ x' ' + \frac rm x' + \frac km x =0 $
Eksempel 2:
En kloss med masse 2,5 kg. ligger på en overflate og er festet til en forankret fjær. Fjærstivheten er 1,25 N/m.
Klossen trekkes ut 0,3 meter mot høyre, fra likevektspunktet, der den slippes. Friksjonstallet er 0,03. Beskriv bevegelsen.
Løsning:
Vi har friksjonen og får dempede svingninger (bevegelsen vil ta slutt).
$ x' ' + \frac rm x' + \frac km x =0 $
DIGITALT
Naturlig vekst
Dersom en størrelse x vokser med tiden, kan det skrives som
<math>\frac{dx}{dt} = kx </math>
der k er en konstant og x = x(t).
Man får
<math>\frac{dx}{x} = kdt \\ \int{\frac{dx}{x}} = \int{kdt} \\ ln|x| = kt +C \\ x=e^{kt}e^C = Ae^{kt}</math>
A er konstanten eC og man observerer at vet tiden t = 0 er A = x, dvs. A =x0
Altså:
<math>x= x_0e^{kt}</math>
Dersom en størrelse avtar, for eksempel aktiviteten i et radioaktivt materiale, har man:
<math>\frac{dN}{dt} = -kN</math>
<math>N(t) = C e^{-kt}</math>
k er isotopavhengig ( dersom modellen representerer aktivitet i radioaktivt materiale).
Eksempel 3:
Et radioaktivt stoff har masse 5 kg. ved tiden t = 0 og minker med 2% per år.
- finn m(t)
Her har vi flere muligheter:
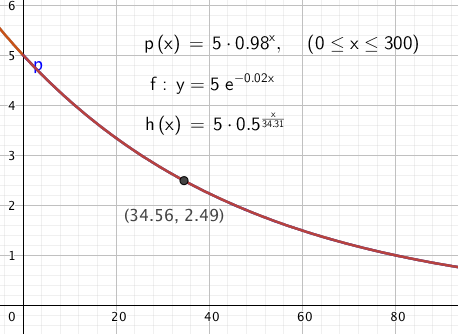
- Differensiallikning $m' = -km \\ m' + km = 0 \\ m \cdot e^{kt} = c \\ m = ce^{-kt} \\ initialbetingelser: \\ m= 5e^{-kt}$
- Med opplysningen om 2% reduksjon kunne man funnet funksjonen uten å gå veien om differensiallikningen:
$M = 5 \cdot 0,98^t = 5 \cdot (e^{\ln0,98})^t \\ M(t) = 5 \cdot e^{-0,0202t}$
k i den første løsningen er altså tilnærmet 0,0202.
Dersom vi ønsker en funksjon som inneholder halveringstiden eksplisitt:
$\frac 12 = ( \frac 12)^{\frac tT}$
Likningen stemmer når t og T er like store. t er tiden og T halveringstiden. Vi finner halveringstiden:
$ \frac 12 = e^{-0,0202t} \\t= \frac{ln 0,5}{-0,0202} = 34,3$
$m(t) = m_0 \cdot ( \frac12)^{\frac{t}{34,3}}$
Alle tre funksjonsuttrykkene gir den samme utviklingen, altså den samme grafen.
Dersom man har en populasjon kan modellen over være egnet til å beskrive veksten i startfasen, men ingen populasjoner vokser i det uendelige. En mer egnet modell kan da være den logistiske.
Logistisk vekst
Man tenker at populasjonsveksten vil stagnere når antall individer nærmer seg det et område kan tåle. Det antall kalles bæreevnen og vil variere ut fra økosystemets forutsetninger. Man kaller bæreevnen for B
Den relative vekstraten
<math> \frac1N \frac{dN}{dt}</math> skal være lik en positiv konstant, multiplisert med forskjellen mellom bæreevne og antall. Man får:
<math> \frac1N \frac{dN}{dt} = a(B-N) \Leftrightarrow \frac{dN}{dt} = aN(B-N)\\ \quad </math>
Delbrøkoppspalting gir:
$\frac{1}{N(B-N)} = \frac{a}{N} + \frac{b}{B - N} \Rightarrow \quad 1 = a(B - N) + bN \Rightarrow a = b = \frac 1B$
$N \neq 0 \wedge N \neq B$
$\int \frac{1}{N(B-N)} dN= \int a dt \Leftrightarrow \frac1B \int(\frac1N + \frac{1}{B-N})dN = \int a dt $
$\frac1B (ln|N|- ln|B-N|)= at + C_1 \Leftrightarrow ln|N| - ln|B-N| = aBt + C, \quad C = C_1B $
$ln|\frac{N}{B-N}|= aBt + C $
$\frac{N}{B-N} = Ke^{aBt}, \quad \quad K = \pm e^C $
Ved tiden t = 0 er <math> N = N_0 </math>
Da er <math>K = \frac{N_0}{B- N_0} </math>
som gir
<math>\frac{N}{B-N}= \frac{N_0e^{aBt}}{B-N_0} </math>
Ved noe regning får man
<math>N(t) = \frac{BN_0}{N_0 +(B-N_0)e^{-aBt}} </math>
( Utregning: $ \quad \frac{N}{B-N}= \frac{N_0e^{aBt}}{B-N_0} \quad \Rightarrow \quad N = \frac{N_0e^{aBt}}{B-N_0} (B-N) \quad \Rightarrow \quad N = \frac{BN_0e^{aBt}}{B-N_0} - \frac{N \cdot N_0e^{aBt}}{B-N_0}$
$N (1+ \frac{N_0e^{aBt}}{B-N_0})= \frac{BN_0e^{aBt}}{B-N_0} \quad \Rightarrow \quad N = \frac{BN_0e^{aBt}}{(B-N_0) (1+ \frac{N_0e^{aBt}}{B-N_0} )}$
$N = \frac{BN_0e^{aBt}}{B+ \frac{BN_0e^{aBt}}{B-N_0} - N_0 - \frac{N_0 \cdot N_0e^{aBt}}{B-N_0} } \quad \Rightarrow \quad N = \frac{BN_0e^{aBt}(B- N_0)}{B(B-N_0)+ BN_0e^{aBt} - N_0 (B-N_0) - N_0 \cdot N_0e^{aBt}}$
$N = \frac{BN_0e^{aBt}(B- N_0)}{B(B-N_0) - N_0 (B-N_0)+ BN_0e^{aBt} - N_0 \cdot N_0e^{aBt}} \quad \Rightarrow \quad N = \frac{BN_0e^{aBt}(B- N_0)}{(B - N_0 )(B-N_0)+ (B - N_0) N_0e^{aBt}} $
$N = \frac{BN_0e^{aBt}}{(B-N_0)+ N_0e^{aBt}} \quad \Rightarrow \quad N = \frac{BN_0}{(B-N_0)e^{-aBt}+ N_0} $
og vi er i mål.)
Eksempel 4:
Newtons avkjølingslov ( og oppvarming)
Hvordan går det egentlig med et legeme med romtemperatur, når den slippes i kokende vann?
T(t) - er objektets temperatur ved tiden t.
Tomg - er omgivelsenes temperatur.
T(0) - er objektets temperatur ved tiden t = 0.
Newtons avkjølingslov sier at temperaturendringen <math>\frac{dT}{dt} </math>
er proporsjonal med differansen mellom T(t) og Tomg, dvs:
<math>\frac{dT}{dt} = k(T(t) - T_{omg})</math>
k er en konstant som blant annet har med legemets varmeledningsevne og geometri å gjøre.
Her har man to muligheter:
Avkjøling
Dersom objektet er varmere enn omgivelsene ved tiden t = 0 har man en avkjølingssituasjon. Da er <math>\frac{dT}{dt} </math> negativ. Det gir:
$ T(t) - T_{omg} > 0 $Oppvarming
Dersom objektet er kaldere enn omgivelsene ved tiden t = 0 har man en oppvarmingssituasjon. Da er <math>\frac{dT}{dt} </math> positiv. Det gir:
<math>T(t) - T_{omg} < 0 </math>Det gir Newtons lov for avkjøling:
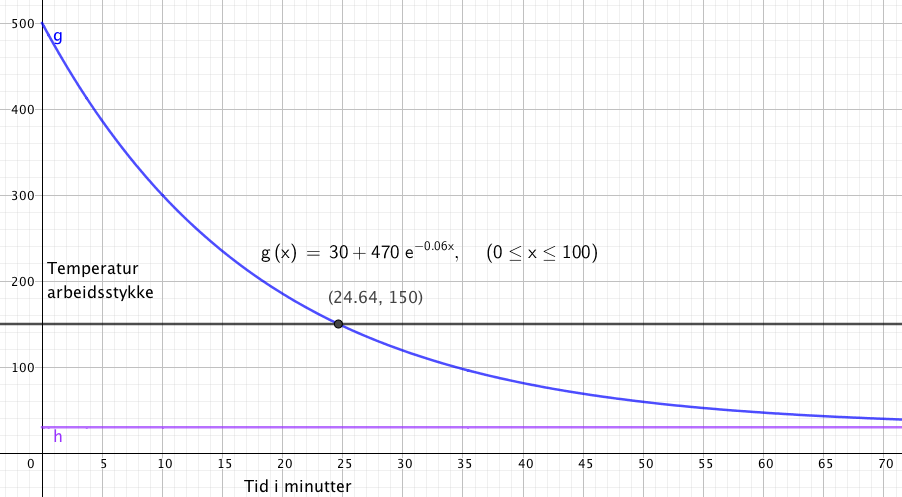
En smed skal bearbeide et stykke metall. Når det tas ut av ovnen er det 500°C. Metallet lar seg bearbeide til det er 150°C. Under denne temperatur er det vanskelig å forme. Smeden har fra tidligere erfaringer funnet ut at metallet avkjøles med 200 grader de første 10 minuttene. I rommet der arbeidet foregår er det 30°C.
Hvor lang tid har smeden på bearbeidingsprosessen? Løsning: Newtons lov for avkjøling sier: $ \frac{dT}{dt} = -k(T(t) - T_{omg}) $I dette tilfellet gir det:
$\frac{dT}{dt} = -k(T(t) - 30)\\ \frac{dT}{dt} = k(30 - T(t))\\ \int ( \frac {1}{30 - T(t)})dT = \int(k)dt\\ - ln |30 - T(t)| = kt + C \\
30 - T(t) = e^{-(kt + C)}$
$ 30 - T(t) = C_2e^{-kt } \\ \hspace{50 mm} der \hspace{5 mm}C_2 \hspace{5 mm}er\hspace{5 mm} e^C \\ T(t) = 30 - C_2e^{-kt } \hspace{50 mm} $
$ T(0) = 500C \\ 30 - 500 = C_2 \\ C_2 = -470 \\ T(t) = 30 + 470 e^{-kt} \\ $
Hva er k?k er en konstant som bestemmes av objektets form og materialegenskaper,
samt omgivelsenes tetthet / varmeledningsegenskaper mm.For å finne k må man benytte seg av smedens erfaringer og kunnskaper:
<math>T(10) = 300C \\ 300 = 30 +470 e^{-10k} \\ ln( \frac {270}{470}) = -10k \\ k = 0,0554 </math>
Det gir funksjonen for avkjøling:<math>
T(t) = 30 +470 e^{-0,0554t}</math> Hvor lang tid har så smeden før arbeidsstykket hans går under 150? <math>150 = 30 + 470 e^{-0,0554t}</math> $t \approx 24, 6 min $ Temperaturforløpet ser slik ut:Konsentrasjon i væsker
Eksempel 6:
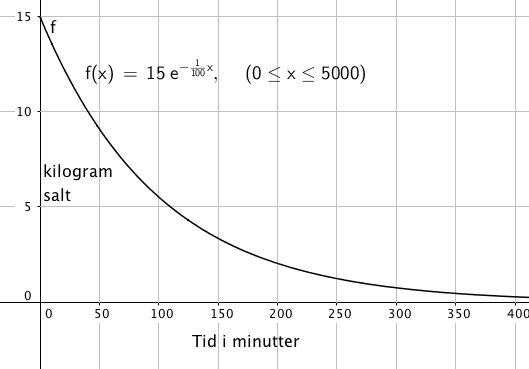
En tank inneholder 1000 liter saltvann, med 15 kg oppløst salt. Rent vann fylles på tanken med en fart på 10 liter / minutt. Blandingen røres hele tiden godt. Samtidig tappes tanken med 10 liter / minutt. Hvor mye salt er det i tanken etter t minutter?
Vi har følgende:
A(t) = saltmengde ved tiden t
Endring av saltmengde $ \frac{dA}{dt}$ = salt inn – salt ut
$\frac{dA}{dt}$ = (konsentrasjon inn $ \frac {g}{L}) \cdot $ (væskestrøm inn $\frac{L}{min}$) - (konsentrasjon ut $ \frac {g}{L}) \cdot $ (væskestrøm ut $\frac {L}{min}$)
$\frac {dA}{dt} = 0 - \frac {A}{1000} \cdot 10 = - \frac{A}{100}$
$\frac {dA}{dt} = - \frac{A}{100} \\ \int \frac 1A dA = \int - \frac{1}{100} dt \\ ln |A| = - \frac {1}{100} t + C \\ e^{ ln |A|} = e^{- \frac {1}{100} t + C} \\ |A| = e^C \cdot e^{- \frac {1}{100} t }$
Initialbetingelser: A(0) = 15 gir:
$A(t) = 15 e^{- \frac {1}{100} t }$
Eksempel 7:
I en vanntank som rommer 1000 liter er det 500 liter ferskvann. Det tilsettes 3 liter per minutt av en vannløsning som inneholder 4 gram salt per liter. Samtidig som det blandes godt, tappes det ut 2 liter per minutt i bunnen av tanken. Finn saltmengden i tanket x(t) ved tiden t.
Vi har:
Saltmengden i tank ved tiden t: x(t)
Salt inn: 4 g / L $\cdot $ 3 L / min = 12 g/ min
Salt ut: $\frac{x(t)}{V(t)} \cdot $ (- 2) L / min
Endring i væskevolum: $\frac{dV}{dt} = 3 - 2 = 1 \\ \int dV = \int 1 dt \\ V(t) = t+C$.
Ved tiden t = 0 var det 500 liter i tanken, så:
V(t) = t + 500.
Det betyr at det tar 500 minutter før tanken er full.
Endring i saltmengde: $\frac{dx}{dt} = 12- 2 \cdot \frac{x(t)}{V(t)} \\ \frac{dx}{dt} = 12- 2 \cdot \frac{x(t)}{t+500} \\ $
Så løser vi likningen:
$x' + \frac{2x}{t+500} = 12 $
Finner integrerende faktor:
$e^{\int \frac {2}{t+ 500}} = e^{2 ln|t + 500|} =e^{ln(t + 500)^2} = (t + 500)^2 $
Multipliserer så alle ledd med integrerende faktor:
$x' \cdot (t + 500)^2 + \frac{2x}{t+500} \cdot (t + 500)^2 = 12 \cdot (t + 500)^2 \\ \int (x \cdot(t +500)^2)' dt = \int12 \cdot (t + 500)^2 dt$
Setter u = t + 500 på høyreside og får du = dt og integrerer.
$x( t+ 500)^2 = \frac {12}{3} (t+ 500)^3 + C \\ x = 4 (t + 500) + \frac {C}{(t + 500)^2}$
For å finne C bruker vi opplysningen om at ved tiden t = 0 var x(0) =0, altså bare ferskvann.
$ x(0)=0 \\ 0= 2000 + \frac {C}{500^2} \\ c= - 2000 \cdot 250000 \\ C = - 500000000$
Det gir oss likningen for vårt spesielle tilfelle:
$x(t)= 4t+ 2000 - \frac {500000000}{(t+500)^2}$