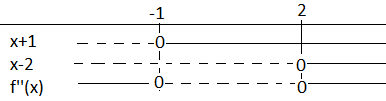R1 2009 vår LØSNING
Del 1
Oppgave 1
a)
1)
<math>f(x) = (x^2+1)^4 \\ f'(x)= 4(x^2+1)^3 \cdot 2x = 8x(x^2+1)^3</math>
(kjerneregelen)
2)
<math>g(x) = xe^{2x} \\ g'(x)= e^{2x}+xe^{2x} \cdot 2 = e^{2x}(1+2x)</math>
(produktregelen)
b)
<math>\lim_{x \to 2} \frac{x^2-2x}{x-2} =\lim_{x \to 2} \frac{x(x-2)}{x-2}=\lim_{x \to 2} x=2</math>
c)
<math> \frac{x-2}{x^2+2x}- \frac{x+2}{x^2-2x}-\frac{4x}{x^2-4} = \\ \frac{x-2}{x(x+2)}- \frac{x+2}{x(x-2)} - \frac{4x}{(x+2)(x-2)} = \\ \frac{(x-2)(x-2)-(x+2)(x+2)- 4x^2}{x(x+2)(x-2)} = \\ \frac{x^2-4x+4-(x^2+4x+4)- 4x^2}{x(x+2)(x-2)} = \\ \frac{- 4x(x+2)}{x(x+2)(x-2)} = \\ -\frac{4}{x-2}</math>
d)
<math> \vec{AB} = [5-(-2), 4-(-1)] = [7,5] \\ \vec{AC} = [4-(-2), 7-(-1)]= [6,8] \\ \vec{BC} = [4-5, 7-4] =[-1,3] </math>
Dersom to vektorer står vinkelrett på hverandre er skalarproduktet lik null.
Det er ikke tilfelle her.
e)
1)<math>f(x)= 2x^3+8x^2+2x-12 \\
f(-1) = 2(1)^3 +8 (1)^2 +2(1)-12 = 2+8+2-12 = 0 \quad</math>
dvs.f(x) er delelig med (x-1)
<math>\quad \quad 2x^3+8x^2+2x-12: (x-1) = 2x^2+10x+12 \\ -(2x^3 -2x^2) \\ \quad \quad\quad\quad \quad\quad \quad 10x^2+2x \\ \quad\quad \quad \quad -(10x^2-10x) \\ \quad \quad\quad \quad\quad \quad\quad \quad\quad\quad\quad\quad\quad 12x-12\\ \quad \quad\quad \quad\quad \quad\quad \quad\quad\quad\quad -(12x-12) \\\quad \quad\quad \quad \quad \quad \quad\quad \quad \quad \quad\quad \quad\quad \quad\quad \quad\quad\quad \quad \quad 0 </math>
<math>2x^2+10x+12 = 0 \\ x= \frac {-10 \pm \sqrt{100-96}}{4} = \frac{-10 \pm 2}{4} \\ x = -3 \vee x= -2 \\ f(x)= 2x^3+8x^2+2x-12 = (x-1)(x+2)(x+3)</math>
2)
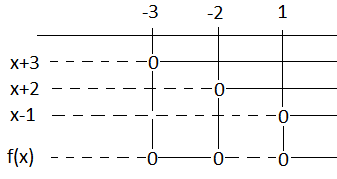
<math>f(x) \leq 0 \\ x \in <\leftarrow, -3] \cup [-2,1]</math>
f)
<math> lg(\frac{1}{a^2}) + 3lga = lg1 - lga^2+3lga = -2lga+3lga = lga</math>
Oppgave 2
a)
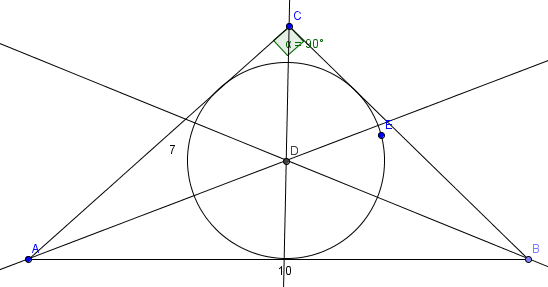
<math>\bigtriangleup ABC \sim \bigtriangleup ADC </math>
Fordi vinkel A er den samme i begge trekanter og vinkel C (i ABC) er lik vinkel D (i ADC).
<math>\bigtriangleup ABC \sim \bigtriangleup BCD </math>
Fordi vinkel B er den samme i begge trekanter og vinkel C (i ABC) er lik vinkel D (i BCD).
b)
<math> \frac{AC}{AB} = \frac{AD}{AC} \\ (AC)^2 = AD \cdot AB </math>
<math> \frac{BC}{AB} = \frac{BD}{BC} \\ (BC)^2 = BD \cdot AB</math>
c)
<math> (AC)^2 = AD \cdot AB \\ (BC)^2 = BD \cdot AB \\ \text{legger sammen likningene} \\ (AC)^2 + (BC)^2 = AB \cdot (AD + DB) \\ (AC)^2 + (BC)^2 = (AB)^2</math>
Del 2
Oppgave 3
a)
b)
<math>(lnx)^2+lnx^2 =3 \\ (lnx)^2+2lnx-3=0 \\ u = lnx \\ u^2+2u-3 =0 \\ u = \frac{-2 \pm \sqrt{4+12}}{2} \\ u = -3 \quad \vee\quad u = 1 \\ lnx=-3 \quad\vee\quad lnx = 1 \\x = e^{-3} \quad\vee\quad x = e</math>
c)
1)
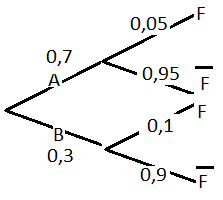
<math>P(F) = P(A)\cdot P(F|A) + P(B) \cdot P(F|B) = 0,7 \cdot 0,05 + 0,3 \cdot 0,1 = 0,065</math>
2)
<math>P(A|F) = \frac{P(A\cap B)}{P(B)} = \frac {0,7 \cdot 0,05}{0,065} = 0,54</math>
Oppgave 4
Alternativ I
a)
<math>f(x) = -x^3+ax^2+bx-11 \\ f'(x) = -3x^2+2ax+b \\ f'(x)=0 \Rightarrow -3-2a+b = 0 \Rightarrow b = 2a+3 \\ f(-1)= -16 \Rightarrow 1+a-b-11 = - 16 \Rightarrow a-b =-6 \\ a- (2a+3) = -6 \\ a =3 \\ b= 2a+3 = 2 \cdot 3 +3 =9 </math>
b)
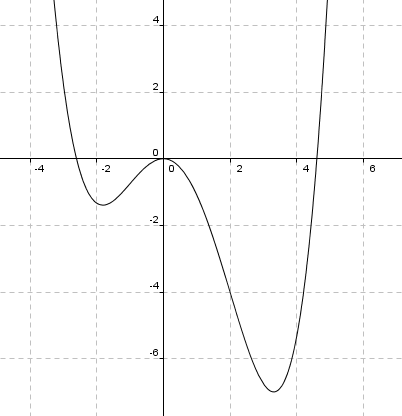
<math>f(x)= -x^3+3x^2+9x-11 \\ f'(x) = -3x^2+6x+9 \\ f'(x)=0 \Rightarrow x=-1 \quad \vee \quad x=3 </math>
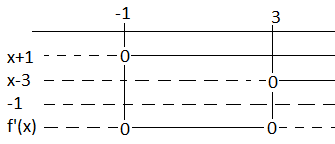
f avtar fra minus uendelig til x = -1 og fra x = 3 til uendelig. f vokser fra x = -1 til x = 3. Bunnpunktet for x=-1 er gitt i oppgaven. Man ser at f i tillegg har et maksimum for x=3.
<math>f(3)= -27+3 \cdot 9 + 9 \cdot 3 - 11 = 16</math>
Maksimumspunkt: (3,16)
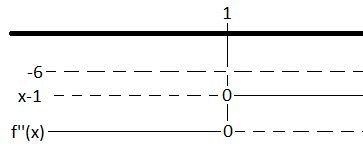
c)
<math>f(x) = -6x+6</math>
Vendepunkt: (1,f(1)) = (1,0)
d)
<math>f'(x)=9 \\ -3x^2+6x+9 =9 \\x(-3x+6)= 0 \\ x=0 \vee x=2 \\ f(0)=-11 \quad \wedge f(2)= 11</math>
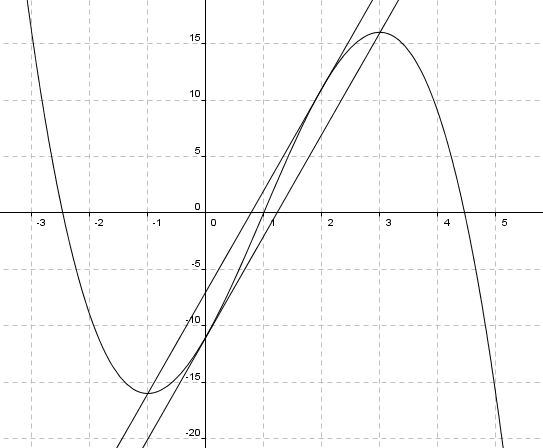
Stigningstall er 9 for begge tangentene. Punktene er henholdsvis (0,-11) og (2,11). Det gir følgende likninger for tangentene:
<math>y =ax+b \\ y= 9x+b \\ -11 = 9 \cdot 0 +b \quad \vee \quad 11 = 9 \cdot 2 + b \\ b= -11 \quad \vee \quad b=-7 \\ \Downarrow \\ y=9x-11 \quad \vee \quad y=9x-7 </math>
e)
Figuren viser grafen til f, sammen med de to tangentene fra oppgave d. Man ser at b må ligge mellom -11 og -7, <-11,-7> for at likningen f(x)= 9x + b skal ha tre løsninger.
Alternativ II
a)
b)
<math>f(x) = \frac{1}{12}(x^4-2x^3-12x^2)\\ f'(x) = \frac 13 x^3 - \frac 12 x^2 - 2x \\f(x)= x^2-x-2</math>
<math> f(-1)= \frac{1}{12}(1+2-12) = - \frac 34 \\ f(2)= \frac{1}{12}( 16-16-12 \cdot 4)= -4</math>
Koordinater for vendepunktene: <math>(-1, - \frac 34) \wedge (2,-4)</math>
c)
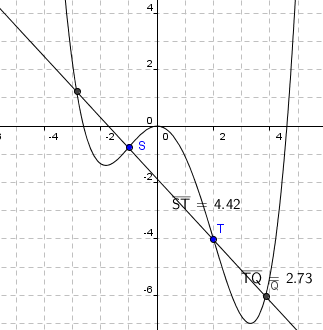
Rett linje gjennom S og T:
y = ax + b
<math> a = \frac{\Delta y}{\Delta x} = = \frac{-4+ \frac 34}{2+1} = - \frac {13}{12}</math>
Bruker punktet (2, -4) og får:
<math> -4 = - \frac{13}{12} \cdot 2 + b \\ y = - \frac{13}{12}x - \frac {11}{6}</math>
Ved inspeksjon (Geogebra) ser man at de to andre skjæringspunktene er (-2,85 , 1,26) og Q = (3,85 , -6,01).
d)
<math>\frac{ST}{TQ} = \frac{4,42}{2,73} = 1,619</math>
e)
<math>g(x) = 12x^2-12</math>
Den dobbelderiverte er null for x lik minus en og for x lik en. Negativ mellom minus en og en, ellers positiv.
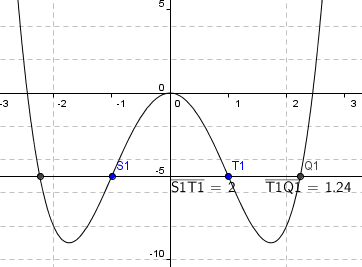
Forholdet blir også her 1,619, det gyllne snitt.
Oppgave 5
a)
<math>\vec{OM_1} = \frac 12 ( \vec{OA}+\vec{OB}) = \frac 12 ( [a,0]+ [b,c]) = \frac 12 [a+b,c] = [\frac{a+b}{2}, \frac c2] </math>
<math>\vec{OM_2} = \frac 12 \vec{OB} = \frac 12 [b,c] = [\frac{b}{2}, \frac c2] </math>
<math>\vec{OM_3} = \frac 12 \vec{OA} = \frac 12 [a,0] = [\frac{a}{2}, 0] </math>
b)
<math> \vec{OS} </math> og <math> \vec{OM_1} </math> er parallelle vektorer. Det vil derfor finnes et tall x som multiplisert med den ene vektoren vil gi den andre vektoren.
<math> \vec{AS} </math> og <math> \vec{AM_2}</math> er parallelle og ved å summere OA vektor med en del av AM2vektor vil man ende opp i S.
c)
<math> \vec{OS} = x \vec{OM_1}\quad \wedge \quad \vec{OS} = \vec{OA} + y \vec{AM_2} \\ x \vec{OM_1}=\vec{OA} + y \vec{AM_2} \\ x\left[\frac{a+b}{2}\quad , \quad \frac c2 \right] = [a,0] + y \left[ \frac{b}{2}-a \quad , \quad \frac c2 \right] \\ x \cdot \frac{a+b}{2} = a + y \cdot \left(\frac b2 - a \right) \quad \wedge \quad x \cdot \frac c2 = y \cdot \frac c2 \\x \cdot \frac c2 = y \cdot \frac c2 \Rightarrow x=y \\ x \cdot \frac{a+b}{2} = a + x \cdot \left(\frac b2 - a \right)\\ x \left( \frac{a+b}{2} - \frac b2 + a \right) =a \\ x(a+b-b+2a)=2a \\ x = \frac 23\\ x=y = \frac 23 </math>
d)
<math>\vec{OS} = \frac 23 \vec{OM_1}= \frac 23 \left[ \frac{a+b}{2}\quad,\quad \frac c2 \right] = \left[ \frac{a+b}{3}\quad, \quad \frac c3 \right]</math>
e)
Medianene i en trekant skjærer hverandre i et punkt som deler medianene i forholdet 2:1, regnet fra hjørnene. Dette er i sammsvar med svarene i c og d.
f)
<math> \vec{OB}= \frac 12 \vec{OA} + 3 \vec{M_2S} = \\[3,0]+ 3[-2,4]= \\ [-3, 12] </math>