R1 2011 høst LØSNING
DEL EN
Oppgave 1:
a
1)
<math>f(t)= 0,02t^3 + 0,6t^2 + 4,1 \\ f'(t)= 0,06t^2 + 1,2t </math>
2)
<math>g(x)= \sqrt{x^2-1} \\g'(x)= \frac {1}{2\sqrt{x^2-1}} \cdot 2x = \frac {x}{\sqrt{x^2-1}}</math>
3)
<math>h(x) = x^2 \cdot e^{2x} \\h'(x) = 2x \cdot e^{2x} + x^2 \cdot 2 \cdot e^{2x} = 2xe^{2x}(1+x)</math>
b
1)
$P(2) =2^3-4 \cdot 2^2 - 4 \cdot 2 + 16 = 8-16-8+16=0 $
Siden P(2) = 0 er x=2 et nullpunkt.
2)
$ \quad( x^3-4x^2-4x+16):(x-2) = x^2 -2x -8 \\ -( x^3-2x^2) \\ \quad \quad -2X^2-4x \\ \quad -(-2x^2+4x) \\ \quad \quad \quad -8x+16 \\ \quad \quad \quad -(-8x+16) $
$x^2-2x-8 =0 \\ x = \frac{2 \pm \sqrt{4+32}}{2} \\ X= -2 \vee x = 4$
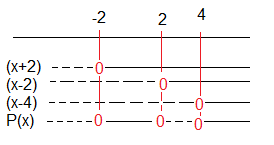
$ x^3-4x^2-4x+16 = (x-2)(x+2)(x-4)$
3)
$P(x) \le 0$
$x \in < \leftarrow, -2] \cup [2, 4]$
c
$ y = a - b^x \\ b^x = a-y \\ x = \frac{lg(a-y)}{lg b}$
y må være mindre enn a fordi man ikke kan ta logaritmen til et negativt tall.
d
1)
$\vec {AB} = [3-1,4-0] = [2,4] \\ \vec{AC} = [2-1, t-0] = [1,t]$
2)
$ \vec{AB} \perp \vec{AC} \\ \vec{AB} \cdot \vec{AC} = 0 \\ [2, 4] \cdot [ 1, t] =0 \\ 2 + 4t =0 \\ t = - \frac 12$
3)
Dersom sirkelen ha AB som diameter er koordinatene til sentrum i sirkelen:
$x = \frac{1+3}{2} =2 \\ y= \frac{0+4}{2}=2 \\ (2,2)$
Radius i sirkelen er en halv ganger lengden av AB vektor. $\frac 12 |\vec{AB}| = \frac{\sqrt{20}}{2} = \sqrt 5$
Likning for sirkel:
$(x-2)^2+(y-2)^2 = (\sqrt 5)^2 \\ (x-2)^2+(y-2)^2 = 5$
e)
1)
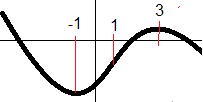
f minker i områdene minus uendelig til -1 og fra 3 til uendelig
f vokser fra -1 til 3.
2)
f har to ekstremalpunkt, et minimumspunkt for x = -1 og et maksimumspunkt for x = 3. Grafen har et vendepunkt for x=1. For verdier mindre enn 1 vender grafen sin hule side opp, og for verdier større enn 1 vender den sin hule side ned.
3)
f)
$f(x)= x^2+1 \\ f ´(x) = \lim_{\Delta x \to 0} \frac {f(x+ \Delta x)- f(x)}{\Delta x} \\ = \lim_{\Delta x \to 0} \frac {((x+ \Delta x)^2 +1)- (x^2+1)}{\Delta x} \\=\lim_{\Delta x \to 0} \frac {x^2 + 2x \Delta x + (\Delta x)^2 + 1 - x^2-1}{\Delta x}\\ = \lim_{\Delta x \to 0} \frac {\Delta x(2x+ \Delta x)}{\Delta x} \\ =\lim_{\Delta x \to 0} 2x +\Delta x = 2x$
g)
1)
Vinkel ADB er en pereferivinkel og skjærer over samme bue som AOB. Vinkel ADB er derfor $30^{\circ}$.
2)
Vinkel DBE er en pereferivinkel som spenner over samme bue som DOE. Vinkel DBE er derfor $10^{\circ}$ .
3)
Vinkelsummen i en trekant er 180 grader. I trekanten BCD er vinkel DBC 10 grader. Vinkel BDC er 180 - 30 = 150 grader. Vinkel ACB må da vare lik 20 grader.
DEL TO
Oppgave 2:
a)
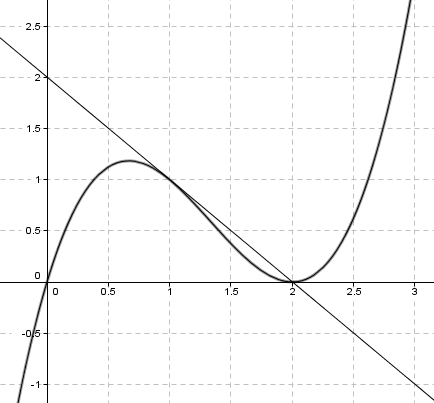
$f(x)= x^3-4x^2+4x \quad x \in <-1, 3> \\ f(x)=0 \\ x^3-4x^2+4x=0 \\ x(x^2-4x+4)=0 \\ x=0 \vee x^2-4x+4 =0 \\ x=0 \vee x= \frac{-(-4) \pm \sqrt{(-4)^2- 4 \cdot 1 \cdot 4}}{2} = 2$
Summen under rottegnet i andregradsformelen er null. Det gir sammenfallende løsning for x = 2, hvilket betyr at grafen til f tangerer x-aksen i punktet (2,0)
b)
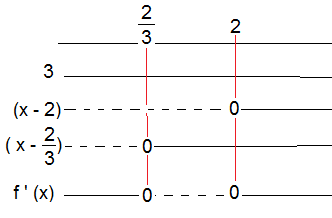
$f ' (x) = 3x^2-8x+4 \\ f ' (x) = 0 \\ x = \frac {8 \pm \sqrt{64 - 48}}{6} \\ x= \frac {8 \pm 4}{6} \\ x = \frac 23 \vee x= 2 \\ f ' (x) = 3(x- \frac 32) (x-2) $
Grafen har et maksimumspunkt for $x=\frac23$ og et minimumspunkt for x = 2.
Maksimumspunkt: $( \frac 23, f( \frac 23)) $ dvs $( \frac 23, \frac{32}{27})$
Minimumspunkt: $( 2, f(2))$ dvs. $ (2,0)$
c)
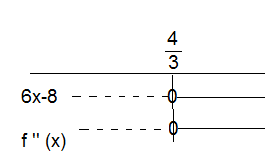
$f ' ' (x) = 6x - 8 \\ f ' ' (x)= 0 \\ 6x-8 =0 \\ x= \frac 43$
Grafen til f vender sin hule side ned for x- verdier mindre enn $\frac 43$ og sin hule side opp for x- verdier større enn $\frac 43$.
Vende punkt i $ ( \frac 43, f( \frac 43))$ som er $ ( \frac 43, \frac {16}{27})$.
d)
$ f(1) = 1 \\ f ' (1) = -1 \\ y = ax + b \\ 1= - 1 + b \\ b = 2 \\ y = -x + 2$
e)
f)
f(x) = -x+2
Med digitale hjelpemidler ser man at denne likningen har løsning for x = 1 eller x = 2. f(2) = 0, dvs. Q har koordinatene (2,0)
Oppgave 3:
a)
1)
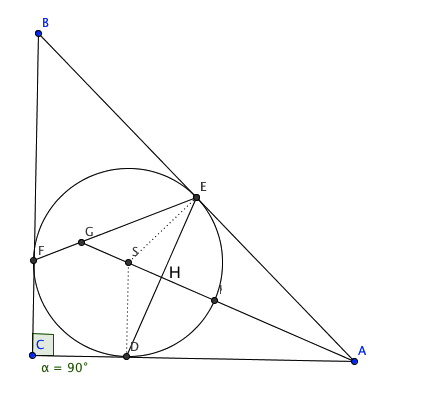
Figuren over viser en skisse av problemet.
Punktet G ligger på linjen som halverer vinkel A. Trekanten AED er likebeint, derfor er DE normal på AG, dvs, vinkel GHE er 90 grader.
2)
Sentralvinkelen DSF spenner over 90 grader. Vinkel HEG er lik periferivinkelen DEF, dvs. 45 grader. Vinkel HGE er 180 grader - 90 grader - 45 grader = 45 grader.
b)
Vi har gjort det digitalt, du gjør det med passer fordi det står i oppgaven. Det betyr bare at du finner midtnormalene til hver av kordene, de vil skjære hverandre i sirkelens sentrum. Se vår figur og eksperimenter.
Oppgave 4:
a)
Sentrum i A:
$x^2+y^2+6x+4y-12=0 \\ (x^2+6x+9) + (y^2+4y+4) -13-9-5 =0 \\ (x+3)^2 + (y+2)^2 =5^2$
Sentrum A = ( -3, -2)
Sentrum i B:
$x^2 + y^2 - 6x - 12y+20 =0 \\ (x^2-6x+ 9) + (y^2-12y+36) +20 -9 - 36 =0 \\ (x-3)^2 + (y-6)^2 =5^2$
Sentrum B = ( 3, 6)
b)
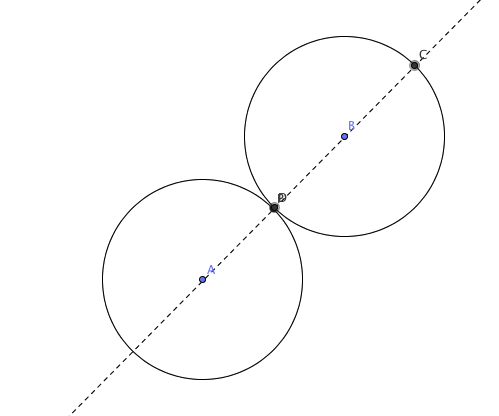
Punktet P er tangeringspunktet mellom sirklene og må ligge på den rette linjen mellom sentrum i de to sirklene.
Begg sirklene har radius 5. Koordinatene til P blir da:
$x= \frac{x_A + x_B}{2} = \frac{-3+3}{2} = 0 \\ y= \frac{y_A + y_B}{2} = \frac{-2+6}{2} = 2$
P har koordinatene ( 0, 2)
c)
Parameterfremmstilling: trenger et punkt og en rettningsvektor.
Rettningsvektor
$\vec{AB}= [ 3-(-3), 6-(-2)] = [6, 8] = 2[3, 4]$
Punkt A= ( -3, 2)
Parameterfremmstilling:
x = -3 + 3t
y = 2 + 4t
d)
$\vec{AC} =\frac 32 \vec{AB} = \frac 32 [6, 8] = [9,12]$
A = (-3, -2)
C blir da ( 9-3, 12-2) = (6,10)
Oppgave 5:
a)
| Jenter | Gutter | Totalt | |
|---|---|---|---|
| Bukse | 60 | 80 | 140 |
| Ikke Bukse | 60 | 0 | 60 |
| Total | 120 | 80 | 200 |
$P( bukse) = \frac{140}{200} = 0,70 = 70$ %
b)
$P bukse | jente) = \frac{60}{120} = 0,50 = 50$ %
$P(bukse | jente ) \neq P(bukse)$. Det betyr at hendelsene er avhengige.
c)
Det står i oppgaven at man skal bruke Bayes formel, men når tallene er organisert i en krysstabell kan det være lettere å plukke sannsynligheten direkte fra tabellen. Vi skal finne sannsynligheten for jente gitt at personen går i bukser.
$P(jente|bukser) = \frac {60}{140} = 0,429 = 42,9$ %
Dersom man bruker Bayes formel får man $P(jente | bukser) = \frac{P(jente) \cdot P(bukse | jente)}{P(bukser)} = \frac {0,6 \cdot 0,5}{0,7} = 0,429 = 42,9 $%
Oppgave 6:
a)
Faktorene som går opp i 28 er 1, 2, 4, 7 og 14. Summen er 1 + 2 + 4 + 7 + 14 = 28. Derfor er 28 det man kaller et perfekt tall.
b)
Faktorene som går opp i 284 er 1, 2, 4, 71 og 142. Summen av disse er 220. Man legger merke til at summen av faktorene i 220 er 284 og summen av faktorene i 284 er 220.