Del 1

Oppgave 1

a)

$f(x)=x^2\cdot \cos(3x)\Rightarrow f'(x)=(x^2)'\cos(3x)+x^2(\cos(3x))'=2x\cos(3x)-3x^2\sin(3x)$

b)

1) Delvis integrasjon gir at $\int 5x\cdot e^{2x}\,dx=5\int x\cdot e^{2x}\,dx=5[\frac{1}{2}xe^{2x}]-\frac{5}{2}\int e^{2x}\,dx=\frac{5}{4}(2x-1)e^{2x}+C$

2) La $u=x^2-1$ så $du=2xdx$, og $\int \frac{6x}{x^2-1}\,dx=\int \frac{3}{u}\,du=3\ln|u|+C=3\ln(|x^2-1|)+C$

c)

Vi multipliserer med integrerende faktor <math>e^{\int -2\,dx}\,\,=e^{-2x}</math> og får at <math>y'e^{-2x}-2e^{-2x}y=3e^{-2x}</math>. Omskrivning av venstresida gir at <math>(ye^{-2x})'=3e^{-2x}</math>. Integrasjon gir at <math>\int (ye^{-2x})'\,dx=ye^{-2x}=\int 3e^{-2x}\,dx=-\frac{3}{2}e^{-2x}+C</math>. Multiplikasjon med <math>e^{2x}</math> gir at <math>y=-\frac{3}{2}+Ce^{2x}</math>. Startbetingelsen gir at <math>y(0)=2=C-\frac32</math>, så <math>C=2+\frac32=\frac{7}{2}</math>, og løsningen på startverdiproblemet blir <math>y=\frac{7}{2}e^{2x}-\frac32</math>

d)

1) <math>\frac12\left(\cos(u-v)+\cos(u+v)\right)=\frac12\left(\cos u \cos v +\sin u \sin v +\cos u \cos v -\sin u \sin v \right)=\cos u \cos v </math>

2) <math>(\cos x)^2=\cos x \cos x =\frac12 \left(\cos(x-x)+\cos(x+x)\right)=\frac12(1+\cos(2x))</math>. Videre er <math>\int (\cos x)^2\,dx=\int \frac12 (1+\cos(2x))\,dx=\frac12\int 1\,dx+\int \frac12 \cos(2x)\,dx=\frac12 x+\frac14\sin(2x)+C</math>

e)

1) <math>\int_{-3}^2 f(x)\,dx=\int_{-3}^2 g'(x)\,dx= g(2)-g(-3)=28-6=22</math>

2) <math>f'(x)=g(x)=h(x)</math>, så <math>\int_{-3}^1 h(x)\,dx=\int_{-3}^1 f'(x)\,dx=f(1)-f(-3)=-2-0=-2</math>

Oppgave 2

a)

<math> \vec{AB} \times \vec{AC} = [12+2,-(-18+4), 3+4]= [14, 14, 7] </math>

b)

Normalvektoren til planet som går gjennom punktene A, B og C er <math> \frac17[14, 14, 7] = [2, 2, 1]</math>

Et vilkårlig punkt i planet er <math>P=(x,y,z)</math>.

<math> \alpha: 2x + 2y + z - 4 = 0 </math>

c)

Siden linjen står vinkelrett på <math>\alpha</math>-planet kan vi bruke <math>[2, 2, 1]</math> som retningsvektor for linjen <math>l</math>. Linjen går gjennom <math>P = (5, 4, 4)</math>. Man får da:

<math>[x,y,z] = [5, 4, 4] + t [2, 2, 1]</math> som er ekvivalent med

$ n: \left [ x = 5+ 2t\\ y = 4 + 2t \\ z = 4 + t \right]$

I xz-planet er y = 0. Parameterfremstillingen for linjen gir da <math>t=-2</math>. Innsatt for x og z gir det koordinatet <math>(1, 0, 2)</math>

d)

Et vilkårlig punkt Q på linjen l er gitt ved parameterfremstillingen for l. Man får:

<math> V_{ABCQ} = \frac16|(\vec{AB} \times \vec {AC}) \cdot \vec{AQ}|</math>

<math> \vec{AQ}= [5+2t-3, 4+2t-0, 4+t+2] = [2t+2, 2t+4, t+6] </math> innsatt i likningen over gir det:

e)

Volumet i pyramiden skal være 42. Innsatt svaret i d gir det $\frac{21}{2}|t+2| = 42$ som gir

$t + 2 = 4$ eller $t + 2 = -4$

<math>t = -6</math> eller <math>t = 2</math>

Man får to løsninger, en "over", og en "under" alfa- planet. Man setter inn i parameterframstillingen for l og får:

<math> Q= ( 9, 8, 6)</math> eller $Q = (-7, -8, - 2)$.

Del 2

Oppgave 3

a)

Karakteristisk ligning er $\lambda^2+\frac25\lambda+\frac{26}{25}=(\lambda+\frac15-i)(\lambda+\frac15+i)=0$. Generell løsning på differensialligninga blir derfor $y(x)=Ae^{(-\frac15-i)x}+Be^{(-\frac15+i)x} $. Eulers formel gir at $e^{-ix}=\cos x -i\sin x $ og $e^{ix}=\cos x +i\sin x $, så $y(x)=Ae^{(-\frac15-i)x}+Be^{(-\frac15+i)x}=Ae^{-\frac15x}(\cos x -i\sin x )+Be^{-\frac15 x}(\cos x +i\sin x )=e^{-0.2x}(C\sin x +D\cos x )$.

b)

$y(0)=5=C\sin 0 +D\cos 0 =D$ og $y(\frac{3\pi}{4})=0=e^{-0.2\cdot \frac{3\pi}{4}}(C\sin(\frac{3\pi}{4})+5\cos(\frac{3\pi}{4}))$. Eksponentialfunksjonen er positiv, så $C\sin(\frac{3\pi}{4})+5\cos(\frac{3\pi}{4})= C\frac{\sqrt{2}}{2}-5\frac{\sqrt{2}}{2}=0$. Altså er $C=5$, og $y(x)=e^{-0.2x}(C\sin x +D\cos x )=5e^{-0.2x}(\sin x +\cos x)$.

Oppgave 4

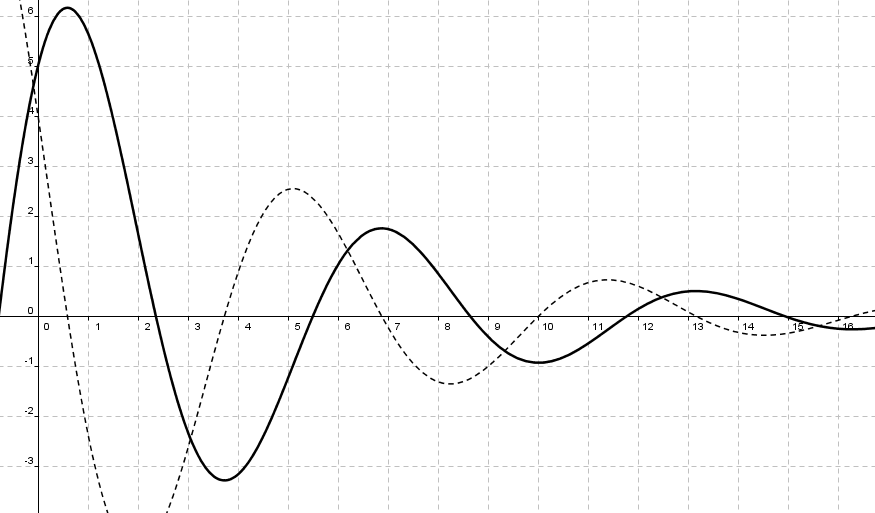
$f(x)=5e^{-0,2x}\cdot(\sin x +\cos x )$ der $x\in\langle 0,15\rangle $

a)

Grafen ser slik ut:

Den deriverte er også med (stiplet) fordi den skal finnes i c).

b)

Nullpunkter

<math> 5e^{-0,2x}</math> kan aldri bli null. Man får

Regner man om fra eksakte verdier til desimaltall, ser man at det stemmer med grafen i a).

c)

<math> \begin{align} f^{\prime}(x) &= 5(-0,2)e^{-0,2x} \cdot (\sin x + \cos x)+5e^{-0,2x} \cdot (\cos x -\sin x) \\ &= -e^{-0,2x} \cdot \sin x -e^{-0,2x} \cdot \cos x +5e^{-0,2x} \cdot \cos x - 5e^{-0,2x} \cdot \sin x \\ &= 4e^{-0,2x} \cdot \cos x - 6e^{-0,2x} \cdot \sin x \\ &=2e^{-0,2x} \cdot (2\cos x-3\sin x) \end{align} </math>

d)

Man har et toppunkt hver gang den deriverte skifter fortegn fra positiv til negativ. Ved å løse <math>2\cos(x)-3\sin(x) = 0</math> og å tegne fortegnslinje, finner man at det er tilfelle for <math>x=0.59</math> , <math>x=6.87</math> og for <math>x= 13.15</math>. Sett disse x-verdiene inn i funksjonsuttrykket og man får funksjonsverdien til toppunktene.

e)

<math> A= \sqrt{a^2 + b^2} = \sqrt2</math> Punktet <math>(1,1)</math> ligger i første kvadrant. <math> \tan\phi = 1</math>. Man får da:

f)

<math>\sin(x + \frac{\pi}{4})</math> varierer i verdi mellom <math>-1</math> og <math>1</math>, avhengig av <math>x</math>. Derfor ligger $f(x)$ mellom $q$ og $p$, altså i området <math> \pm 5\sqrt{2}e^{-0,2x}</math>

Oppgave 5

a)

Eksponentialfunksjonen er alltid positiv, så for å finne nullpunktene må vi løse ligningen $\sin x +\cos x =0$. Denne kan omskrives til $\frac{\sin x }{\cos x }=\tan x =-1$, så $x=\tan^{-1}(-1)=-\frac{\pi}{4}+n\pi=\frac{3\pi}{4}+(n-1)\pi\approx 2.356+(n-1)\pi$

b)

Nullpunktene danner en aritmetisk progresjon på formen $a_n=a_1+(n-1)d$. Dersom $n=10$ er $x_{10}=2.356+9\pi\approx 30.63$, så vi må ha at $1\leq n\leq 9$. Altså er det $9$ nullpunkt i intervallet $x\in\langle 0,30\rangle$

c)

Toppunktene kan skrives $5e^{-0.2x}, 5e^{-0.2(x+2\pi)}, 5e^{-0.2(x+4\pi)}$, altså på formen $ak^n=5e^{-0.2x}(e^{-0.4\pi})^n$, der $a=5e^{-0.4x}=6.164$ og $n=0,1,2$. Det neste leddet i følgen blir dermed $6.164 (e^{-0.4\pi})^3\approx 0.142$.

d)

Vi får rekka $\sum_{n=0}^{\infty} 6.164(e^{-0.4\pi})^n$. Siden $|e^{-0.4\pi}|\approx 0.285<1$ vil rekka konvergere.

Summeformelen for geometriske rekker gir at $\sum_{n=0}^{\infty} 6.164(e^{-0.4\pi})^n\approx 6.164\lim_{n\to\infty}\frac{1-0.285^n}{1-0.285}\approx 8.62$

Oppgave 6

Alternativ I

a)

Siden <math>v=y'</math> og <math>a=y</math> kan vi skrive ligningen <math>-b\cdot v-k\cdot y=m\cdot a</math> som <math>-b\cdot y'-k\cdot y=m\cdot y</math>. Vi deler med <math>m</math> og får at <math>y+\frac{b}{m}y'+\frac{k}{m}y=0</math>

b)

Med $b=1$, $k=2.6$ og $m=2.5$ blir ligningen

$y^{\prime \prime}+\frac{1}{2.5}y'+\frac{2.6}{2.5}y=y^{\prime\prime}+\frac{2}{5}y'+\frac{26}{25}y=0$

Fra 3b) vet vi at løsningen på startverdiproblemet er $y(t)=5e^{-0.2t}(\sin t +\cos t )$

c)

<math>\sin(t)+\cos(t)</math> er periodisk med periode <math>2\pi</math>, og avstanden mellom nullpunktene er <math>\pi</math>.

d)

Forholdet mellom to påfølgende maksimale utslag er <math>\frac{5e^{-0.2(t+2\pi)}}{5e^{-0.2t}}=e^{-0.4\pi}\approx 0.285</math>, så det maksimale utslaget minker med <math>1-0.285=0.715=71.5\%</math>

Alternativ II

a)

La <math>S_n=\sum_{k=1}^n k</math>. Vi grupperer tallene i par <math>\{1,n\}, \{2,n-1\},...</math>. Det er <math>\frac{n}{2}</math> slike par og summen i hvert par er <math>n+1</math>, altså blir <math>S_n=\frac{n}{2}\cdot (n+1)=\frac{n(n+1)}{2}</math>

b)

Ved bruk av digitalt verktøy beregner vi at <math>s_{15}=14400</math> og <math>s_{16}=18496</math>, så vi behøver <math>16</math> ledd for å overstige <math>15000</math>.

c)

Induksjonssteg 1: <math>1=\frac{1^2\cdot 2^2}{4}</math>, så formelen er riktig for <math>n=1</math>.

Induksjonssteg 2: Anta at formelen er riktig for <math>n=k</math>. Da er <math>s_k=\frac{k^2(k+1)^2}{4}</math>, og <math>s_{k+1}=s_k+(k+1)^3=\frac{k^2(k+1)^2}{4}+(k+1)^3=(\frac{k^2}{4}+k+1)(k+1)^2=\frac{k^2+4k+4}{4}(k+1)^2=\frac{(k+1)^2(k+2)^2}{4}</math>, så formelen er riktig for <math>n=k+1</math>. Det følger at formelen er riktig for alle naturlige tall.

d)

R2 2010 vår LØSNING