R2 2012 høst LØSNING
Del 1
Oppgave 1
a)
$f(x) = e^x \cos x $
Produktregelen for derivasjon gir at
$f'(x) = e^x\cos x -e^x\sin x =e^x \left (\cos x -\sin x \right)$
b)
$g(x) = 5(1+\sin x)^3$
Potensregelen og kjerneregelen for derivasjon gir at
$g'(x) = 15(1+\sin x)^2\cdot \cos x$
Oppgave 2
a)
$\int \cos x \cdot (1+\sin x)^3 \, dx$
La $u=\sin x$. Da er $du = \cos x \,dx$. Integralet blir dermed
$\int (1+u)^3 \,du = \frac14(1+u)^4+C=\frac14 (1+\sin x)^4+C$, der $C$ er en integrasjonskonstant.
b)
$\int_1^e x\ln x \,dx$
Vi bruker delvis integrasjon. Det gir
$\int_1^e x\ln x\,dx = [\frac12 x^2 \ln x]_1^e-\int_1^e \frac12 x\,dx = \frac12 e^2 - \frac14 [x^2]_1^e = \frac14 e^2+\frac14$
Oppgave 3
a)
Vi har gitt punktene $A(1,1,1)$, $B(2,1,5)$ og $C(3,7,3)$, som vi betrakter som vektorer. Da er sidene i $\triangle ABC$
$B-A = (2,1,5)-(1,1,1)=(1,0,4)$, $C-A=(3,7,3)-(1,1,1)=(2,6,2)$ og $C-B=(3,7,3)-(2,1,5)=(1,6,-2)$.
Siden prikkproduktene mellom hvert par av sider (betraktet som vektorer) er ulik $0$, er ingen av vinklene rette, altså er ikke trekanten rettvinklet.
b)
$$ \overrightarrow{OD} = \overrightarrow{OA} + \overrightarrow{AD} = \overrightarrow{OA} + \overrightarrow{BC} \\ = [1, 1, 1]+[1, 6, -2] = [2, 7, -1] \\ D(2,7, -1) $$
Oppgave 4
a)
Vi har gitt ligningen $y^{\prime\prime} - y = 0$.
Karakteristisk ligning blir derfor $\lambda^2=1$, med løsninger $\lambda=\pm 1$. Løsningen blir derfor
$y=C_1 e^{x}+C_2 e^{-x}$.
b)
Initialverdiene $y(0)=5$ og $y'(0)=-1$ er gitt. Setter vi disse inn i løsningen fra forrige deloppgave får vi
$y(0)=C_1+C_2 = 5 \\ y'(0)=C_1-C_2 = -1$
Legger vi sammen de to ligningene får vi
$2C_1 = 4$, så $C_1=2$. Da er $C_2=5-C_1=5-2=3$.
Oppgave 5
Vi har gitt den uendelige rekken $1+\frac13+\frac19 +\frac{1}{27}+\cdots$.
Den kan skrives som $\sum_{n=0}^{\infty}(\frac{1}{3})^n$, som vi gjenkjenner som en geometrisk rekke.
Det er kjent at geometriske rekker $\sum_{n=0}^{\infty}r^n$ konvergerer dersom $|r|<1$. Siden $\frac13 < 1$ vil rekken konvergere.
Formelen for geometriske rekker er $\sum_{n=0}^{\infty}r^n = \frac{1}{1-r} $. Altså er
$\sum_{n=0}^{\infty}(\frac{1}{3})^n=\frac{1}{1-\frac13}=\frac{3}{2}$
Oppgave 6
Vi har gitt den periodiske funksjonen $f(x)=a\sin(cx+\varphi)+d$. Vi kan uten tap av generalitet anta at $a>0$:
For $a<0$ kan vi redefinere konstanten til $-a$ og flytte $-1$ innenfor $\sin$.
For å finne $c$ legger vi merke til at $5c+\varphi -(3c+\varphi)= \pi $, altså er $c=\frac{\pi}{2}$. Videre er $\frac{5\pi}{2}+\varphi=\frac{\pi}{2}$, altså er $\varphi = -2\pi$, men siden $\sin(x+2\pi)=\sin x$ kan vi like gjerne velge $\varphi = 0$.
For å finne $a$ og $d$, legger vi nå merke til at $f(0)=5=d$. I toppunktet er til slutt $f(5)=a+5=8$, så $a=3$.
Funksjonen blir derfor $f(x)=3\sin(\frac{\pi}{2}x)+5$.
Oppgave 7
a)
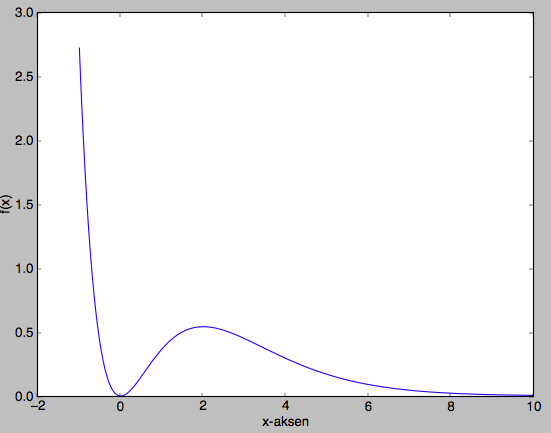
Funksjonen $f(x)=x^2e^{-x}$ er gitt. Topp- og bunnpunkt er bestemt ved å løse $f'(x)=0$. Vi har at $f'(x)=2xe^{-x}-x^2e^{-x}=0$, altså er $x(2-x)=0$ som gir at $x=0$ eller $x=2$. Fra grafen i deloppgaven under ser vi at $x=2$ er et toppunkt og $x=0$ et bunnpunkt.
b)
Oppgave 8
Vi har gitt formelen $\sum_{i=1}^n i(i+3) = \frac{n(n+1)(n+5)}{3}$ som skal bevises med induksjon.
Først ser vi at formelen er riktig for $n=1$, siden $1\cdot (1+3) = 4 = \frac{1\cdot 2\cdot 6}{3}$
Anta at formelen er riktig for en bestemt $n$. Vi legger til neste ledd av summen på hver side og får
$\sum_{i=1}^{n+1} i(i+3) = \frac{n(n+1)(n+5)}{3}+(n+1)(n+4)=\frac{(n+1)(n(n+5)+3(n+4))}{3}=\frac{(n+1)(n^2+8n+12)}{3}$.
Siden $(n+2)(n+6)=n^2+8n+12$, ser vi at $\frac{(n+1)(n^2+8n+12)}{3}=\frac{(n+1(n+2)(n+6)}{3}$. Altså er
$\sum_{i=1}^{n+1} i(i+3)=\frac{(n+1(n+2)(n+6)}{3}$, så formelen er riktig for $n+1$. Altså er formelen riktig for alle positive heltall $n$.
Del 2
Oppgave 1
a)
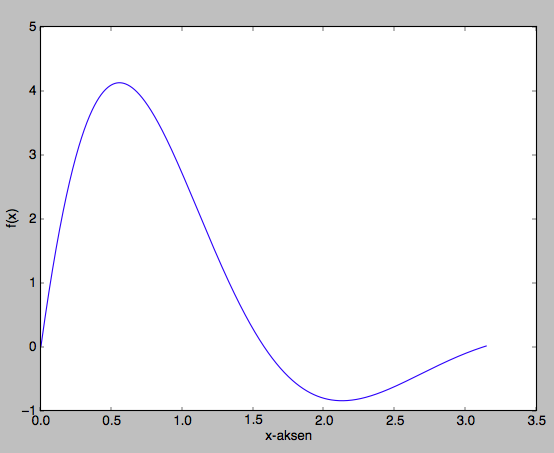
Nullpunkt finnes ved å løse $8e^{-x}\sin 2x=0$. Siden eksponensialfunksjonen er positiv overalt er der nok å betrakte $\sin 2x = 0$, som er tilfelle når $x=\frac{\pi}{2}$.
Topp- og bunnpunkt finner vi ved å løse $f'(x)=0$. Vi har at $f'(x) = -8e^{-x}\sin 2x + 16e^{-x}\cos 2x = 0$. Altså $2\cos 2x = \sin 2x$. Dette er det samme som at $\tan 2x = 2$ eller $x=\frac12(\pi n + \arctan 2)$ for heltall $n$. Fra grafen ser vi at $x=\frac12 \arctan 2\approx 0.55$ svarer til toppunktet, mens $x=\frac12 (\pi+\arctan 2)\approx 2.12$ svarer til bunnpunktet.
Vendepunkt finnes ved å dobbeltderivere $f(x)$. Vi har at $f^{\prime\prime}(x) = (f'(x))' = -8 e^{-x} (4 \cos 2 x+3\sin 2 x )$. Den dobbeltderiverte er $0$ når $4 \cos 2 x+3\sin 2 x = 0$, altså når $\tan 2x = -\frac43$. Da er $x= \frac12 (\pi n + \arctan -\frac43)$ for heltall $n$. Innenfor det aktuelle intervallet ser vi at vendepunktene forekommer for $x= \frac12 (\pi + \arctan -\frac43)\approx 1.11$ og $x= \frac12 (2\pi + \arctan -\frac43)\approx 2.68$.
b)
$\int f(x)\,dx = 8\int e^{-x}\sin 2x \, dx$. Vi identifiserer $a=-1$ og $b=2$ i den oppgitte formelen. Altså er
$\int f(x)\, dx = \frac{8e^{-x}}{5}(-\sin 2x-2\cos 2x) + 8C$
Deriverer vi $\frac{8e^{-x}}{5}(-\sin 2x-2\cos 2x) + 8C$ får vi nå
$-\frac85 (-e^{-x}\sin 2x + 2e^{-x}\cos 2x) -\frac{16}{5}(-e^{-x}\cos 2x-2e^{-x}\sin 2x)=(\frac85+\frac{32}{5})e^{-x}\sin 2x+(-\frac{16}{5}+\frac{16}{5})e^{-x}\cos 2x=8e^{-x}\sin 2x$
c)
Det samlede arealet blir $\int_0^{\frac{\pi}{2}}f(x)\,dx - \int_{\frac{\pi}{2}}^{\pi}f(x)\,dx$. Bruker vi formelen fra forrige deloppgave blir dette
$[\frac{8e^{-x}}{5}(-\sin 2x -2\cos 2x)]_0^{\frac{\pi}{2}}-[\frac{8e^{-x}}{5}(-\sin 2x -2\cos 2x)]_{\frac{\pi}{2}}^{\pi}=\frac{16}{5}(e^{-\frac{\pi}{2}}+1)+\frac{16}{5}e^{-\frac{\pi}{2}}+\frac{16}{5}e^{-\pi}\approx 4.67$
Oppgave 2
a)
Diff.ligningen $v^\prime = 12.0-1.15v$ er gitt. Dette er en separabel ligning som kan skrives $\int_{0}^{v(t)}\frac{dv}{12.0-1.15v} = \int_0^t ds$. Utfører vi integrasjonene får vi at dette blir $\frac{1}{-1.15}[\ln (12.0-1.15v)]_{0}^{v(t)}=t$. $\ln (\frac{12.0-1.15v(t)}{12.0})=-1.15t$, som er det samme som $1-\frac{1.15}{12.0}v(t) = e^{-1.15t}$. Isolerer vi $v(t)$ får vi nå at $v(t) = \frac{12.0}{1.15}(1-e^{-1.15t})$. Løsningen verifiseres ved innsetting i diff.ligningen.
b)
Siden $s^\prime (t) = v(t)$, er $s(t) = \int_0^t v(s)\,ds = \int_0^t \frac{12.0}{1.15}(1-e^{-1.15s})\, ds = [\frac{12.0}{1.15}(s+\frac{1}{1.15}e^{-1.15s})]_0^t= \frac{12.0}{1.15}(t+\frac{1}{1.15}(e^{-1.15t}-1))$
c)
Vi må løse ligningen $100= s(t) = \frac{12.0}{1.15}(t+\frac{1}{1.15}(e^{-1.15t}-1))$. Vi kan omskrive denne til $\frac{115}{12} = t+\frac{1}{1.15}(e^{-1.15t}-1)$. Denne ligningen er vanskelig å løse analytisk, så vi må benytte numeriske metoder. Vi kan f.eks. finne det positive nullpunktet til funksjonen $f(t)=t+\frac{1}{1.15}(e^{-1.15t}-1)-\frac{115}{12}$ med kalkulatoren. Plotter vi funksjonen finner vi at nullpunktet er $\approx 10.45$. Dette virker realistisk når vi sammenligner med 100m-tidene på internasjonalt nivå.
Oppgave 3
a)
1) Dersom $\vec{a}\cdot \vec{b}=0$ må $\vec{a}$ og $\vec{b}$ stå vinkelrett på hverandre.
2) Dersom $\vec{a}\times \vec{b}=0$ må $\vec{a}$ og $\vec{b}$ være parallelle.
3) Dersom $\vec{a}\cdot (\vec{b}\times \vec{c})=0$ må enten $\vec{a}$ og $\vec{b}\times \vec{c}$ stå vinkelrett på hverandre, eller $\vec{b}$ og $\vec{c}$ være parallelle.
b)
Vi har at $(\vec{a}\times \vec{b})^2 = |\vec{a}|^2|\vec{b}|^2\sin^2 \theta$ og $\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos \theta$. Altså er $(\vec{a}\times \vec{b})^2+(\vec{a}\cdot \vec{b})^2 = |\vec{a}|^2|\vec{b}|^2\sin^2 \theta+|\vec{a}|^2|\vec{b}|^2\cos^2 \theta=|\vec{a}|^2|\vec{b}|^2(\sin^2 \theta+\cos^2 \theta)=|\vec{a}|^2|\vec{b}|^2$
c)
Arealet av trekanten er $A=|\vec{a}\times \vec{b}|=\sqrt{(\vec{a}\times \vec{b})^2}=\sqrt{|\vec{a}|^2|\vec{b}|^2- (\vec{a}\cdot \vec{b})^2}$, der vi har brukt formelen fra forrige deloppgave.
Dersom $\vec{a}\cdot \vec{b}=0$ er vektorene $\vec{a}$ og $\vec{b}$ vinkelrette. Da er trekanten rettvinklet, så arealet blir $\frac12|\vec{a}||\vec{b}|$. Dersom $\vec{a}\times \vec{b}=0$ må $\vec{a}$ og $\vec{b}$ være parallelle, så trekanten er degenerert, dvs. at to av hjørnene ligger på en linje, så arealet er $0$.
d)
Vi har at $\vec{a}=[2,3,4]-[1,1,1]=[1,2,3]$ og $\vec{b}=[3,1,5]-[1,1,1]=[2,0,4]$. Da er $\vec{a}\cdot \vec{b}=[1,2,3]\cdot [2,0,4]=2+12=14$,
$|\vec{a}|=\sqrt{1+4+9}=\sqrt{14}$ og $|\vec{b}|=\sqrt{4+16}=\sqrt{20}$.
Arealformelen fra forrige deloppgave gir nå at $A=\frac12 \sqrt{14\cdot 20-14^2}=\frac12 \sqrt{84} = \sqrt{21}$
Oppgave 4
a)
Rekken $1+3+5+\cdots + (2n-1)$ har $n$ ledd med gjennomsnitt $\frac{2n-1+1}{2}=n$. Altså er summen $S_n=n^2$. For at $S_n=n^2=1600$, må $n=\sqrt{1600}=40$.
b)
Rekken kan skrives som $\sum_{i=0}^{\infty} (\frac{1}{4})^i$, altså en geometrisk rekke. Siden $|\frac14|<1$ er rekken konvergent, og konvergerer mot $\frac{1}{1-\frac14}=\frac{4}{3}$.
Oppgave 5
a)
Ellipsen $(\frac{x}{a})^2+(\frac{y}{b})^2=1$ er gitt. Vi flytter over det første leddet og ganger hele ligningen med $b^2$ og får $y^2=b^2-\frac{b^2 x^2}{a^2}$
b)
Volumet av rotasjonslegemet er $\int_{-a}^a \pi y^2\,dx = \pi\int_{-a}^a b^2-\frac{b^2 x^2}{a^2}\,dx =2ab^2\pi - \frac{\pi b^2}{3a^2}[x^3]_{-a}^a=\frac{4}{3}\pi ab^2$
Oppgave 6
a)
Ligningen til en tangent er generelt $y=\alpha x+\beta$. Stigningstallet $\alpha=f^\prime (a)=\frac{1}{2\sqrt{a-2}}$ Tangenten må gå gjennom punktet $P(a,f(a))=(a,\sqrt{a-2})$, så $\sqrt{a-2} = \frac{a}{2\sqrt{a-2}}+\beta$, altså er $\beta = \sqrt{a-2}- \frac{a}{2\sqrt{a-2}} = \frac{a-4}{2\sqrt{a-2}}$.
Punktet $A$ er bestemt av at tangentlinjen skjærer x-aksen, altså må $y=0$ i $A$. Setter vi inn $y=0$ i ligningen for tangenten får vi x-koordinaten til $A$. Vi får $0 = \frac{x}{2\sqrt{a-2}}+\frac{a-4}{2\sqrt{a-2}}$, altså er $x=4-a$. Så $A(4-a,0)$. Videre er $B(x,f(x))$ der $f(x)=0$, altså må $\sqrt{x-2}=0$, som gir at $x=2$. Derfor er $B(2,0)$. Til slutt er $C(a,0)$.
b)
$\int_2^a \sqrt{x-2}\,dx = [\frac23(x-2)^{\frac32}]_2^a = \frac23 (a-2)^{\frac32}$.
Arealet av $\triangle ACP$ er $A=\frac12 f(a)(a-(4-a))=\sqrt{a-2}(a-2)=(a-2)^{\frac32}$
c)
Dette er åpenbart fra de beregningene vi har gjort i forrige deloppgave. Arealet til trekanten er $(a-2)^{\frac32}$. Området under grafen til $f$ er $\frac23(a-2)^{\frac32}$, så arealet av det andre området innenfor trekanten er $(a-2)^{\frac32}-\frac23(a-2)^{\frac32}=\frac13(a-2)^{\frac32}$. Altså er området under grafen dobbelt så stort som det andre området.