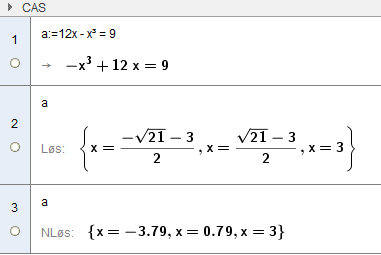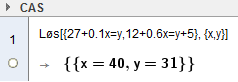S1 2013 høst LØSNING
DEL EN
Oppgave 1
$f(x)= 3x^2- 3x+1 \qquad D_f = \R \\f'(x)= 6x-3 \\f´(2)= 6 \cdot 2 -3 = 9$
Oppgave 2
a)
$x(x+5)-10 =4 \\ x^2+5x-14=0 \\ x= \frac{-5\pm \sqrt{25+56}}{2} \\x= -7 \vee x=2$
b)
$10^{3x} -100000 =0 \\ 10^{3x} = 10^5 \\ 3x=5 \\ x=\frac 53$
Oppgave 3
<math> \left[ \begin{align*} y = x^2+2\\ y+x^2=4 \end{align*}\right] </math>
<math>\left[ \begin{align*} x^2+2+x^2-4=0 \\ 2(x^2-1) =0 \\ x=-1 \vee x=1\end{align*}\right] </math>
$x=-1 \Rightarrow y=3 \\ x=1 \Rightarrow y=3 \\ (-1,3 ) \wedge (1,3)$
Oppgave 4
a)
$v=v_0+at \\t = \frac{v-v_0}{a}$
b)
$t = \frac{v-v_0}{a} \\ t = \frac{25-1}{3}=8 $
Oppgave 5
a)
$ \frac{9^2a^2b^3}{(3ab^2)^2} \\ =\frac{3^4a^2b^3}{3^2a^2b^4} \\ = 3^{4-2} \cdot a^{2-2} \cdot b^{3-4} \\ = 3^2b^{-1} \\ = \frac{9}{b} $
b)
$\lg (\frac{a^2}{b^2}) + \lg( \frac {b^2}{a}) + \lg (a+b) \\ =\lg a^2 - \lg b^2 + \lg b^2 - \lg a + \lg (a+b) \\= 2\lg a - \lg a + \lg(a+b) \\ = \lg a + \lg (a+b) \\ = \lg (a(a+b)) \\ =\lg (a^2+ab)$
Oppgave 6
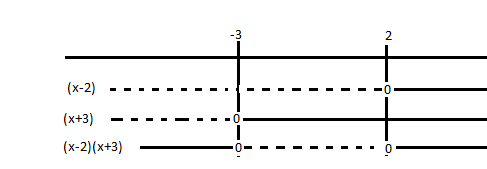
$x^2+2x \ge x+6 \\ x^2+x-6 \ge 0 \\ x= \frac{1 \pm \sqrt{25}}{2} \\ (x-2)(x+3)\ge 0$
$x \in <\leftarrow, -3] \cup [2, \rightarrow> $
Oppgave 7
<math> \left[ \begin{align*} 21+x = y\\ y+2x = 126 \end{align*}\right] </math>
$ 21+x+2x= 126 \\ 3x= 105 \\ x= 35 \\ y= x+21 = 56 \\ x= 35 \wedge y= 56 $
Oppgave 8
$ f(x)=x^3-6x^2 \qquad D_f = \R$
a)
Nullpunkt:
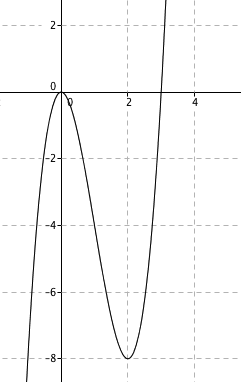
$f(x)= 0 \\ 2x^3 - 6x^2 =0 \\ 2x^2(x-3) =0 \\ x=0 \vee x= 3 \\ f(0) =0 \wedge f(3)= 0$
Nullpunkt i (0, 0) og (3, 0)
b)
Ekstremalpunkt:
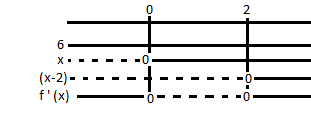
$f´(x) = 6x^2-12x \\ f´(x)=0 \\ 6x(x-2)=0 \\ x= 0 \vee x=2 \\ f(0) = 0 \wedge f(2)=-8$
Maksimumspunkt: (0,0)
Minimumspunkt: (2, -8)
c)
Oppgave 9
$f(0)=-2 \Rightarrow b=2 \\ f(-1) =0 \Rightarrow a=2 $
Vertikal asymptote: $x=1 \Rightarrow c=1$
Funksjonen blir da:
$f(x)= \frac{ax+b}{cx -1} = \frac{2x+2}{x-1}$
Oppgave 10
$f(x) = x^2 \\ f'(x) = lim_{x \to 0} \frac {f(x+ \Delta x) - f(x)}{\Delta x} \\ = lim_{x \to 0} \frac {(x+\Delta x )^2 - x^2}{\Delta x} \\ = lim_{x \to 0} \frac {x^2 +2x\delta x + (\Delta x)^2 - x^2}{\Delta x} \\ = lim_{x \to 0} \frac { \Delta x (2x + \Delta x)}{\Delta x} \\ = 2x$
DEL TO
Oppgave 1
a)
$ \frac{\binom{7}{2} \binom{43}{8}}{\binom{50}{10}} = 0,2964$
Det er 29,6 % sannsynlig at to av lyspærene er defekte.
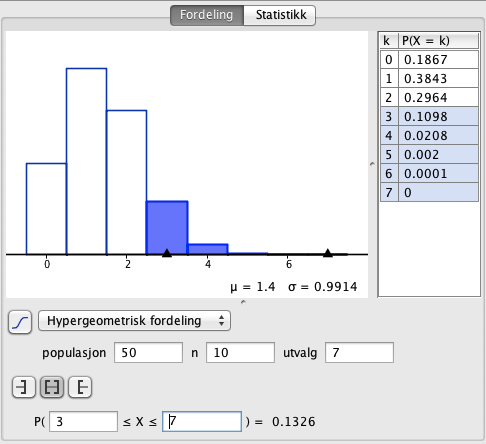
b)
Det er 13,3% sannsynlig at man velger ut minst tre defekte lyspærer.
Oppgave 2
a)
Atten av tjue lyspærer lyser:
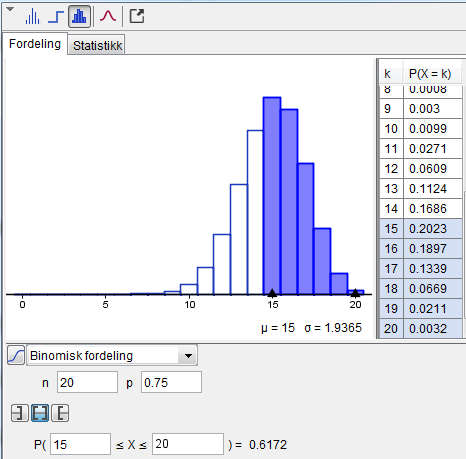
$ P(X=18) = \binom{20}{18} \cdot 0,75^{18} \cdot 0.25^2 = 0.0669 $
Det er 6,7% sannsynlig at 18 pærer lyser.
b)
Det er 61,7% sannsynlig at minst 15 pærer lyser i 1000 timer.
c)
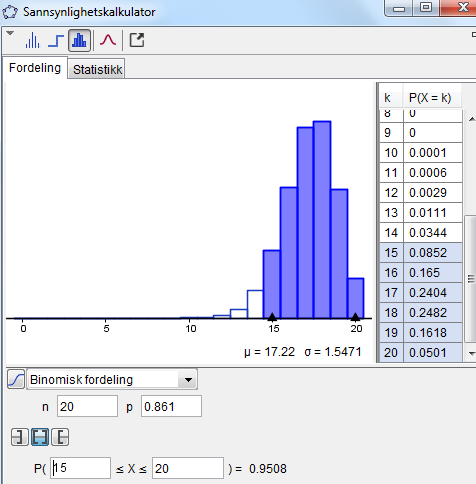
Kunden ønsker: $ P(x \geq 15) \geq 0,95 :$
$ \binom{20}{15} \cdot p^{15} \cdot (1-p)^5 \geq 0,95 $
Ved å prøve seg fram på sannsynlighetskalkulatoren i Geogebra, finner man at den enkelte lyspære må ha en sannsynlighet på p = 0.861.
Oppgave 3
$900 \cdot 1,10^x = 1500 \cdot k^x \\ x=10 \\ (\frac{1,10}{k})^{10} = \frac{15}{9} \\ \frac{1,10}{k} = \pm \root 10 \of{\frac{15}{9}} \\ k = \pm 1,04522$
Oppgave 4
a)
Lengden AB = 2x
Bredden BC = f(x)
Areal $A=F(x) = 2x \cdot f(x) = 2x(6 - \frac 12x^2 )= 12x - x^3$
Arealet må være større enn null:
$F(x)>0 \\ 12x -x^3 >0 \\ x> 0 \wedge x< 3,46 \\ D_F = <0, 3,46>$
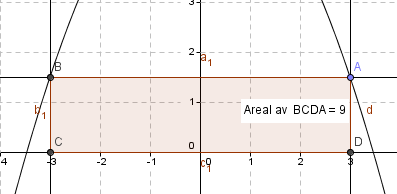
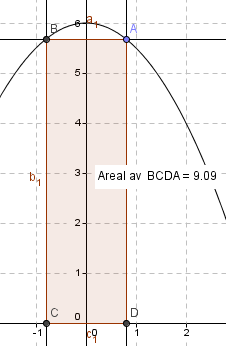
b)
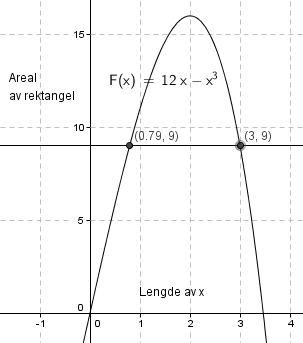
Figurene viser de to mulige rektanglene som begge har areal lik 9. Det gir x = 0,79, eller x = 3.
Alternativt kan oppgaven løses med CAS:
Må her forkaste første løsningsforslag fordi x > 0.
Eller ved å bruke F(x):
Vi observerer godt samsvar mellom de tre metodene.
c)
$F'(x) 12-3x^2 \\ 12-2x^2=0 \\ x^2=4 \\ x = \pm 2$
Når x= 2, dvs sidene i rektangelet er 4, er arealet lik 16. Figuren er da et kvadrat.
d)
Omkrets:
$O(x)= 4x+ 2 \cdot(6- \frac12x^2 \\ O(x) = -x^2 +4x +12 $
Maksimum omkrets:
$O'(x)= -2x+4 \\ -2x+4 =0 \\ x= 2$
Den maksimale omkretsen får vi når figuren er et kvadrat, et spesialtilfelle av et rektangel.
Oppgave 5
a)
$x^2<4 \Rightarrow x> -2$
Dersom kvadratet av x skal være mindre enn 4, må $x \in < -2, 2>$. Implikasjonen er riktig.
b)
$x>-2 \Rightarrow x^2<4$
Dersom x overstiger 2 impliserer det at kvadratet av x overstiger 4. Implikasjonen er feil.
Oppgave 6
a)
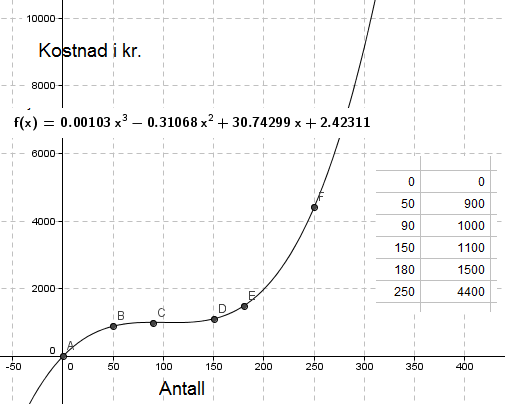
En polynomfunksjon av tredje grad som passer til punktene er:
$K(x)= 0,00103x^3-0,31068x^2+30,74299x + 2,42311$
b)
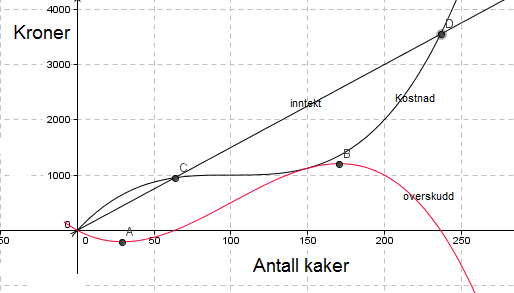
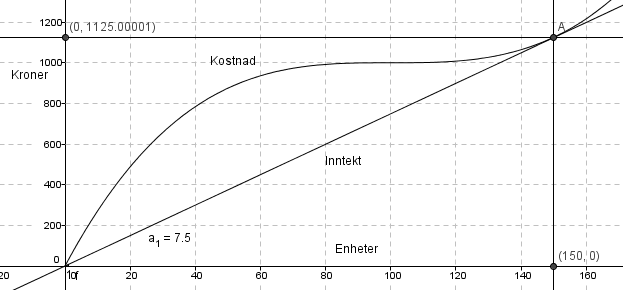
Dersom produksjonen ligger i område 0- 63, eller over 236, har bedriften et underskudd. Når antallet ligger i område 64 - 236 er det et overskudd.
c)
$O(x)= I(x)-K(x) \\ O(x) = 15x-(0,001x^3-0,3x^2+30x) \\ O(x)= -0,001x^3+0,3x^2-15x \\ O'(x)= -0,003x^2+0,6x+15 \\ O'(x)=0 \Rightarrow -003x^2+0,6x-15=0 \\ x = \frac{-0,6 \pm \sqrt{0,6^2-4 \cdot 15 \cdot 0,003}}{- 2 \cdot 0,003} \\ x=171$
Vi forkaster den andre løsningen for x. Fra grafen i a ser vi at det er x= 171 som gir oss maksimum, den andre gir oss minimum.
Når det produseres 171 kaker er overskuddet:
$O(171)= -0,001 \cdot 171^3 + 0,3 \cdot 171^2 -15 \cdot 171 \\ O(171) = 1207$
Altså ca 1207 kroner i overskudd når det produseres 171 kaker.
d)
Dersom kakene koster kroner 7,50 per stykk er det balanse mellom intekter og kostnader når det produseres 150 stykker.
Oppgave 7
a)
Type 1 = x
Type 2 = y
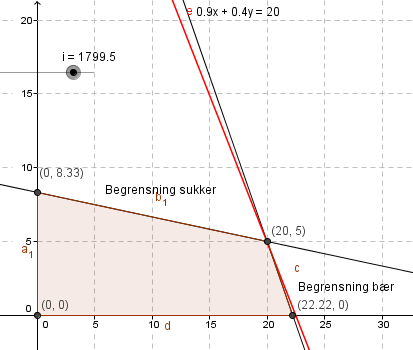
$0,9x+0,4y = 20 \\0,1x + 0,6y =5 \\ x = \frac{5-0,6y}{0,1} \\ x=50-6y \\ 0,9(50-6y) + 0,4y =20 \\ 25=5y \\ y=5 \wedge x=20$
Hun må lage 20 glass av type 1 og 5 glass av type 2.
b)
Inntekter: 80 kr /glass av type 1, 40 kr/glass av type 2. Inntekter blir da 1800 kr.
c)
Løser likningsettet i CAS.
Kiloprisen på sukker må være 40 kroner. Det koster da 31 kroner å lage type en og 36 kroner å lage type to.