S1 2018 høst LØSNING
Diskusjon av denne oppgaven på matteprat
Løsning laget av Marius Nilsen ved Bergen Private Gymnas
DEL 1
Oppgave 1
a)
$x^2-3x+1=3x+8 \\ x^2-6x-7=0 \\ x=\frac{6\pm\sqrt{(-6)^2-4\cdot(-7)}}{2} \\ x=\frac{6\pm 8}{2} \\ x_1=-1 \vee x_2=7$
b)
$lg(x^4)-lg(x^3)+lg(x^2)-lg\,x=6 \\ 4\,lg\,x-3\,lg\,x+2\,lg\,x-lg\,x=6 \\ 2\,lg\,x=6 \\ lg\,x=3 \\ x=10^3\\ x=1000$
c)
$10\cdot 4^x=5\cdot 2^x \\ \frac{2^{2x}}{2^x} = \frac{5}{10} \\ 2^{2x-x} = \frac{1}{2} \\ 2^x = 2^{-1} \\ x=-1$
Oppgave 2
a)
$(a+2b)^2-(2b-a)^2 \\ = (a^2+4ab+4b^2)-(4b^2-4ab+a^2) \\ = a^2+4ab+4b^2 - 4b^2+4ab-a^2\\ = 8ab$
b)
$3^3 \cdot 3^0 + 3^{-1}+3^{-2}+3^{-3} \\ = 27 \cdot 1 + \frac{1}{3}+ \frac{1}{3^2}+ \frac{1}{3^3} \\= 27+ \frac{9}{27}+ \frac{3}{27}+ \frac{1}{27} \\=27 + \frac{13}{27}$
Jeg synes dette svaret er penest, men man kan også skrive svaret slik:
$ 27 + \frac{13}{27}=\frac{729}{27} + \frac{13}{27} = \frac{742}{27} $
Oppgave 3
$x^2-6x \geq 7$
Løser likningen $x^2-6x-7=0$. Kjenner igjen denne likningen fra oppgave 1a). Løsningen er $x_1=-1 \vee x_2=7$
Et andregradsuttrykk $ax^2+bx+c$ med nullpunkter $x_1$ og $x_2$ kan faktoriseres slik: $ax^2+bx+c=a(x-x_1)(x-x_2)$
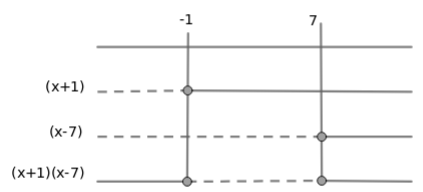
Faktoriserer andregradsfunksjonen: $x^2-6x-7 = (x+1)\cdot(x-7)$
Lager fortegnsskjema:
Svar:
$x^2-6x \geq 7$ når $x \leq -1 \vee x \geq 7$
Alternativt kan svaret skrives slik:
$x \in \langle \leftarrow,-1] \cup [7,\rightarrow \rangle $
Velg din favoritt!
Oppgave 4
a)
b)
Bruker hypergeometrisk sannynlighet, og leser av binomialkoeffisientene i Pascals trekant. (Eksempel: $\binom{7}{4}$ finner du i rad nr.7 og tall nr.4 i raden. Husk å begynne å telle på rad nr.0 og tall nr.0. Hvis du har talt riktig finner du at $\binom{7}{4}=35$).
$P(2J\cap2G)=\frac{\binom{4}{2}\cdot \binom{3}{2}}{\binom{7}{4}}=\frac{6\cdot3}{35}=\frac{18}{35}$
Sannsynligheten for at det blir trukket ut to jenter og to gutter er $\frac{18}{35}$
c)
P(minst en gutt) = 1 - P(ingen gutter) = $1-\frac{\binom{4}{4}\cdot \binom{3}{0}}{\binom{7}{4}}=1-\frac{1\cdot1}{35}=\frac{35}{35}-\frac{1}{35}=\frac{34}{35}$
Sannsynligheten for at minst én gutt fra elevrådet blir med på turen er $\frac{34}{35}$
Oppgave 5
a)
<math> \left[ \begin{align*} x+y = 1 \\ -2x + y = -5 \end{align*}\right] </math>
Trekker likning II fra likning I og får:
$x-(-2x) + (y-y) = 1-(-5) \\ 3x = 6 \\ x=2$
Setter inn $x=2 $ i likning I og får:
$2+y=1 \\ y=-1$
Løsning: $x=2 \wedge y=-1$
b)
Uttrykker de to første ulikhetene med hensyn på y:
Ulikhet nr. 1:
$x-2y \geq -8 \\ y \leq \frac{-x-8}{-2} \\ y \leq \frac{x}{2} + 4$
NB: husk å snu ulikhetstegnet når du ganger eller deler en ulikhet med et negativt tall.
Ulikhet nr. 2:
$x+y \geq 1 \\ y \geq -x+1$
Vi har nå de tre ulikhetene:
$y \leq \frac{x}{2} + 4 \\ y \geq -x+1 \\ y\geq 2x-5$
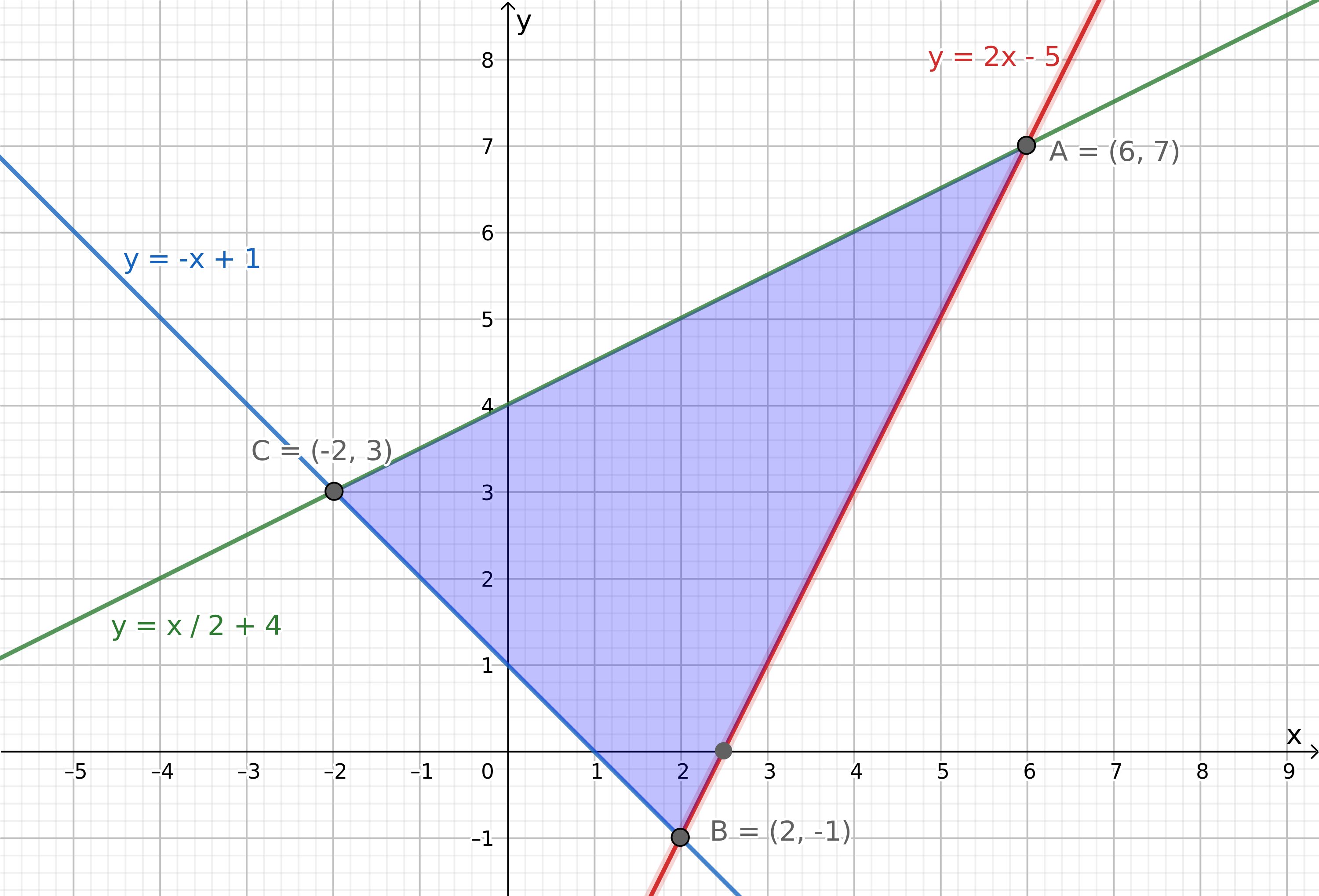
Tegn de tre linjene $y=\frac{x}{2}+4,\,y=-x+1,\,y=2x-5$ (for hånd siden det er del 1). Legg godt merke til hvilken vei ulikhetstegnet er i de fire ulikhetene, og skraver området som avgrenses av disse.
c)
Sjekker verdien til $3x-y$ i punkt A,B og C.
Punkt A: $3\cdot 6-7=11$
Punkt B: $3\cdot 2-(-1)=7$
Punkt C: $3\cdot (-2)-3=-9$
Størrelsen $3x-y$ har størst verdi i punktet (6,7). Da er verdien 11.
Oppgave 6
a)
$O(x)=-0,25x^2+10x-75 \\ O'(x)=-0,5x+10$
Setter $O'(x)=0 for å finne toppunktet$
$-0,5x+10=0 \\ -0,5x=-10 \\ x=20$
Siden O er en andregradsfunksjon med negativt andregradsledd, vet jeg at funksjonen har et toppunkt, og ikke et bunnpunkt. Den produksjonsmengden som gir størst overskudd er 20 enheter per dag. Finner overskuddet $O(20)$
$O(20)=-0,25\cdot 20^2+10\cdot 20 - 75 = -0,25\cdot 400+200-75 = -100+200-75=25$
Overskuddet blir 25 000 kr.
b)
Setter $O(x)=0$ for å finne nullpunktene. Bruker abc-formelen for å løse likningen.
$-0,25x^2+10x-75=0 \\ x=\frac{-10\pm \sqrt{10^2-4 \cdot (-0,25) \cdot (-75)}}{2\cdot(-0,25)} \\ x=\frac{-10\pm \sqrt{100-75}}{-0,5} \\ x_1=\frac{-10+5}{-0,5} \vee x_2=\frac{-10-5}{-0,5} \\ x_1=10 \vee x_2=30$
Det vil bli overskudd for en daglig produksjon mellom 10 og 30 enheter. Siden O er en andregradsfunksjon med toppunkt på x=20, vet jeg at funksjonen har en positiv verdi fra x=10 til x=30.
Oppgave 7
a)
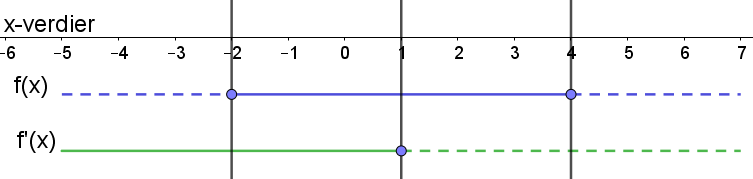
Leser av de aktuelle punktene grafisk: (-1,5) og (2,8).
Gjennomsnittlig vekstfart i intervallet [-1,2]:
$a=\frac{(y_2-y_1}{x_2-x_1}=\frac{8-5}{2-(-1)}=\frac{3}{3}=1$
Gjennomsnittlig vekstfart i intervallet [-1,2] er 1.
b)
$f'(-1)=4$ fordi den momentane vekstfarten i punktet $(-1, f(-1))$ tilsvarer vekstfarten til tangenten. Jeg ser at tangenten går fra punktet (-1,5) til (0,9). Det vil si at vekstfarten til tangenten er 4.
$f'(1)=0$ fordi jeg ser at x=1 er toppunktet til funksjonen. Den momentane vekstfarten i toppunktet er alltid 0.
c)
Oppgave 8
$f(x)=-x^2+2x+8$
Setter $f(x)=0$ for å finne nullpunktene (Punkt A og B). Bruker abc-formelen for å løse likningen.
$-x^2+2x+8=0 \\ x=\frac{-2\pm \sqrt{2^2-4 \cdot (-1) \cdot 8}}{2\cdot(-1)} \\ x=\frac{-2\pm \sqrt{36}}{-2} \\ x_1=\frac{-2+6}{-2} \vee x_2=\frac{-2-6}{-2} \\ x_1=-2 \vee x_2=4$
Lengden $AB=4-(-2)=6$
Arealet av trekant ABC: $A=\frac{6 \cdot f(t)}{2}$
Ønsker en trekant med areal lik 24. Setter A=24 og finner f(t):
$\frac{6\cdot f(t)}{2}=24 \\ f(t)=\frac{24\cdot 2}{6}=8$
Ønsker å finne en t-verdi som gir f(t)=8.
$-t^2+2t+8=8 \\ -t^2+2t=0 \\ -t(t-2)=0 \\ t=0 \vee t=2$
For at arealet til trekanten ABC skal bli lik 24, må vi ha t=0 eller t=2. Punkt C blir enten (0,8) eller (2,8).
DEL 2
Oppgave 1
Bruker CAS i Geogebra.
Den ordinære prisen for en voksenbillett er 90 kroner, og den ordinære prisen for en barnebillett er 45 kroner.
Oppgave 2
a)
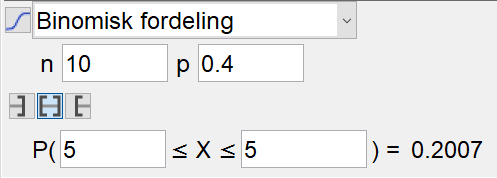
Bruker sannsynlighetskalkulatoren i Geogebra.
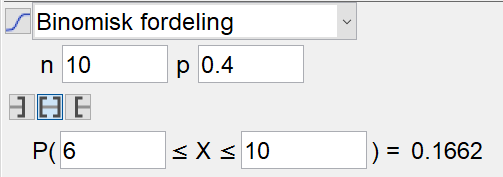
Bruker binomisk sannsynlighetsfordeling, fordi hendelsene er uavhengige, har to utfall, og har fast sannsynlighet.
Sannsynligheten for at halvparten av plantene til Astrid får gule blomster, altså at 5 av de 10 plantene har gule blomster, er ca. 20%.
b)
Sannsynligheten for at flere enn fem av plantene til Astrid får gule blomster er ca. 16,6%.
c)
Dette blir et uordnet utvalg uten tilbakelegging. Jeg finner antall kombinasjoner av de fire plantene med gul blomst, på de 10 plassene.
Stian kan plassere plantene med de gule blomstene på 210 ulike måter.
Oppgave 3
a)
$x\geq 0$ fordi Morten må spise minimum 0 gram makrell i tomat. Han kan ikke spise et negativt antall gram makrell i tomat.
$y \geq 0$ fordi Morten må spise minimum 0 gram syltetøy. Han kan ikke spise et negativt antall gram syltetøy.
For maksimalt energiinnhold gjelder følgende ulikhet (energiinnhold i 4 brødskiver, x gram makrell i tomat, og y gram syltetøy):
$50 \cdot 4 \cdot \frac{900}{100} + \frac{1049}{100} x + \frac{740}{100} y \leq 2400 \\ 1800 + 10,49x+7,40y \leq 2400 \\ 10,49x+7,40y \leq 600$
For maksimalt fettinnhold gjelder følgende ulikhet (fettinnhold i 4 brødskiver, x gram makrell i tomat, og y gram syltetøy):
$50 \cdot 4 \cdot \frac{2,0}{100} + \frac{20,5}{100} x + \frac{0,1}{100} y \leq 12 \\ 4 + 0,205x+0,001y \leq 12 \\ 0,205x+0,001y \leq 8$
For maksimalt karbohydratinnhold gjelder følgende ulikhet (karbohydratinnhold i 4 brødskiver, x gram makrell i tomat, og y gram syltetøy):
$50 \cdot 4 \cdot \frac{32,5}{100} + \frac{3,0}{100} x + \frac{42,4}{100} y \leq 80 \\ 65 + 0,03x+0,424y \leq 80 \\ 0,03x + 0,424y \leq 15$
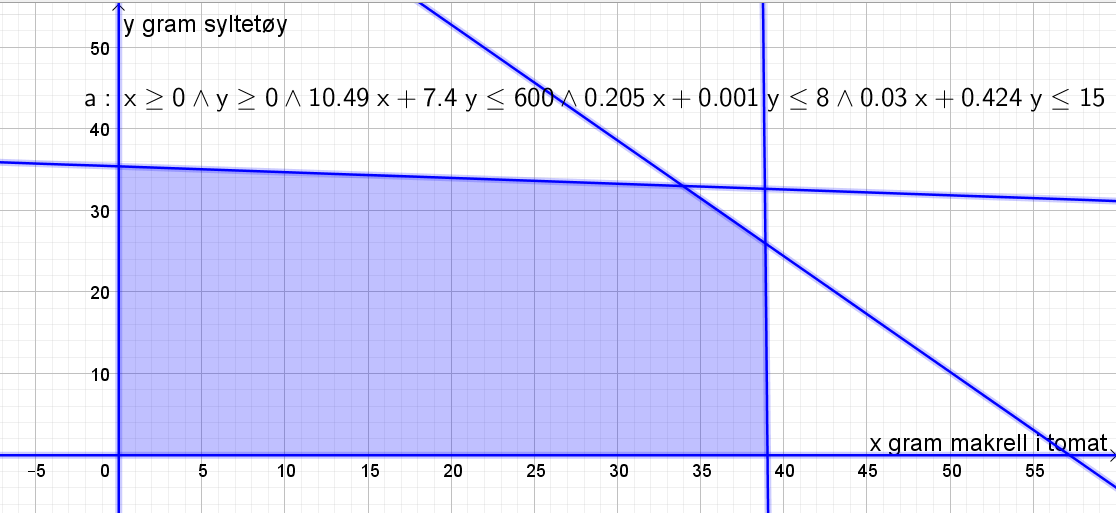
b)
Legger inn ulikhetene i Geogebra.
c)
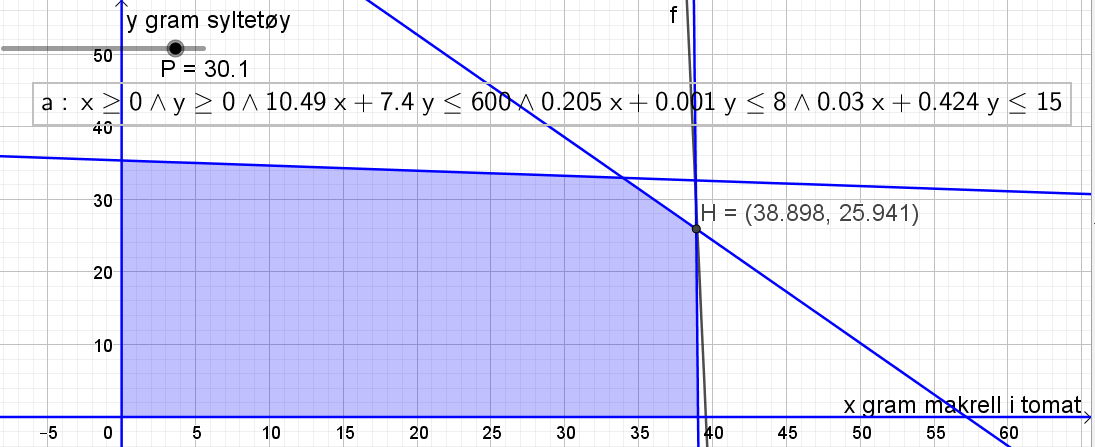
Lager glider for maksimalt proteininnhold (proteininnhold i 4 brødskiver, x gram makrell i tomat, og y gram syltetøy):
$50 \cdot 4 \cdot \frac{12,4}{100} + \frac{13,4}{100} x + \frac{0,3}{100} y = P \\ 24,8 + 0,134x+0,003y = P $
Finner "hjørnene" i det skraverte området ved å bruke kommandoen "toppunkt( <ulikhet> )". Legger inn glideren f i Geogebra og finner punktet på det skraverte området som gir høyest mulig proteininnhold. Dette er i punkt H=(38.9, 25.9). Jeg har skjult de punktene jeg ikke trenger.
Morten kan spise ca. 25,9 gram syltetøy til frokost.
Oppgave 4
a)
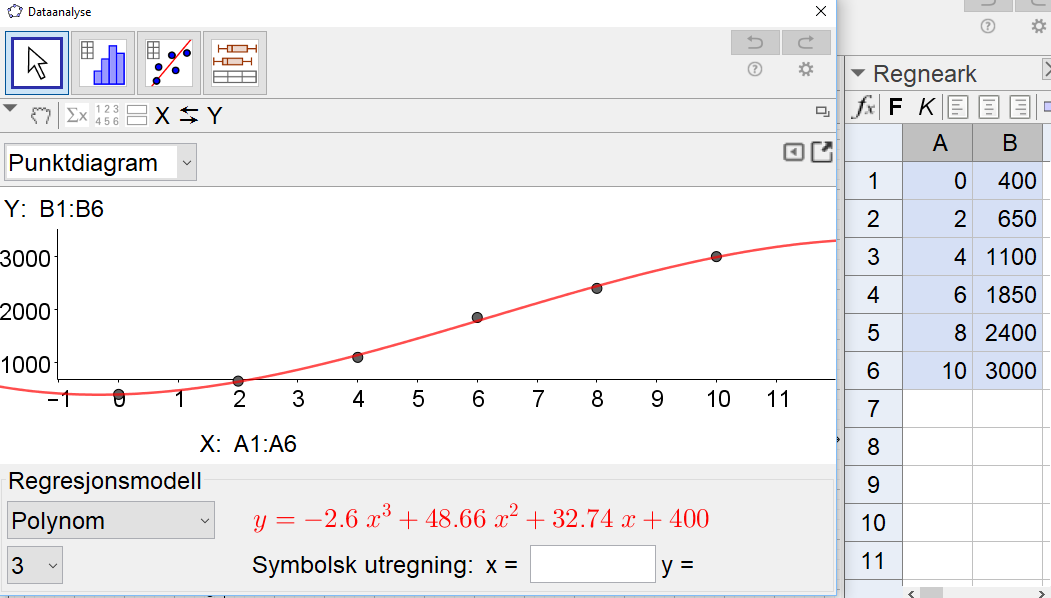
Legger inn antall år etter 2007 og antall dyr i Regnearket i Geogebra. Bruker deretter Regresjonsanalyse og velger Polynom av grad 3.
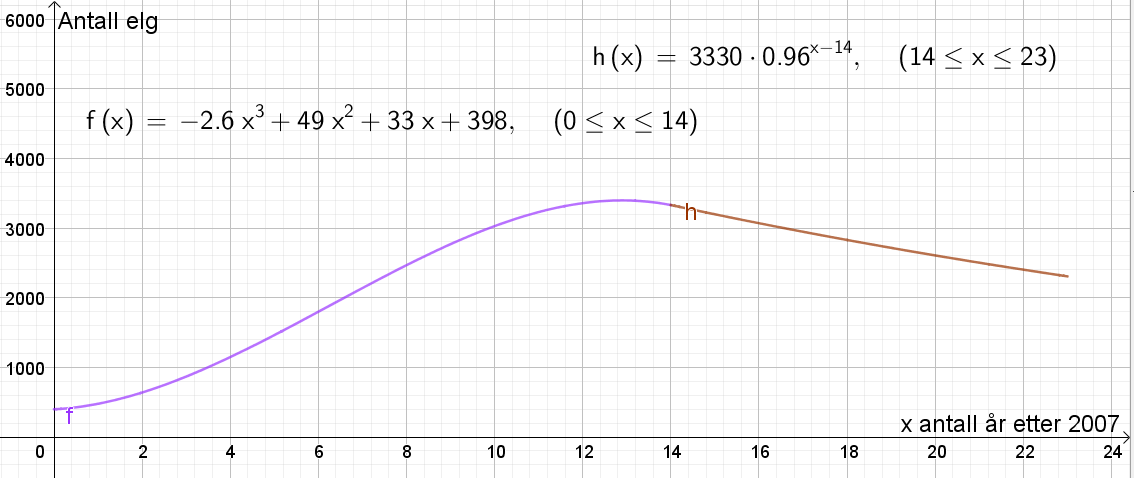
$g(x)=-2,6x^3+48,66x^2+32,74x+400$ kan brukes som modell for antall elg i dette området.
b)
I år 2021, altå 14 år etter 2007, er elgbestanden $f(14)=3329,6 \approx 3330$. Deretter får elgbestanden en årlig nedgang på 4%. Vekstfaktoren er altså 0,96. Vi kan angi antall elg etter 2021 ved eksponentialfunksjonen $h(x)=3330\cdot 0,96^{x-14}$, hvor 3300 er elgbestanden i 2021, 0,96 er vekstfaktoren og x-14 er antall år etter 2021 (x er fremdeles antall år etter 2007, og 2021 er 14 år senere).
c)
d)
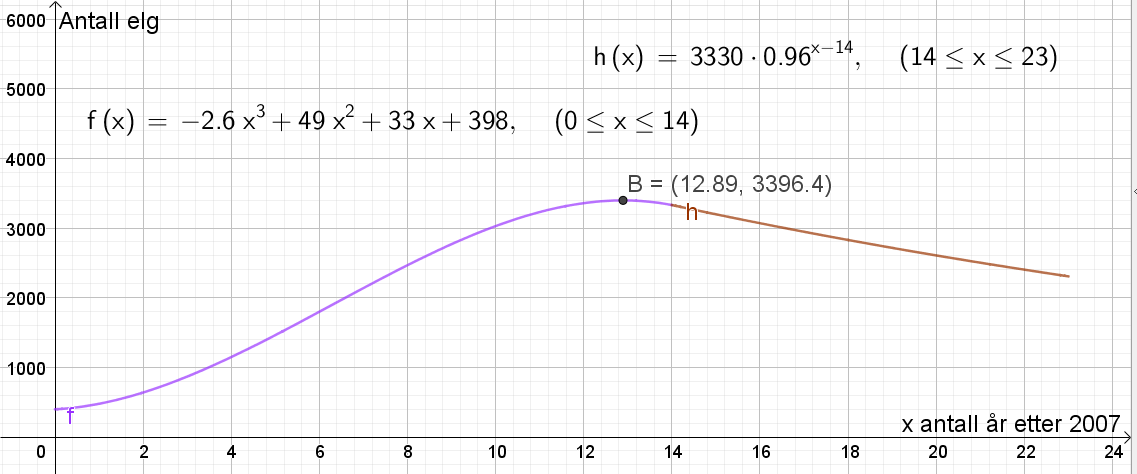
Ser at toppunktet ligger på funksjonen f. Finner toppunktet ved å bruke kommandoen Ekstermalpunkt(f), og får punktet B=(12.89, 3396.4).
Ifølge modellene f og h er elgbestanden er størst 12,89 år etter 2007, altså i år 2019.
e)
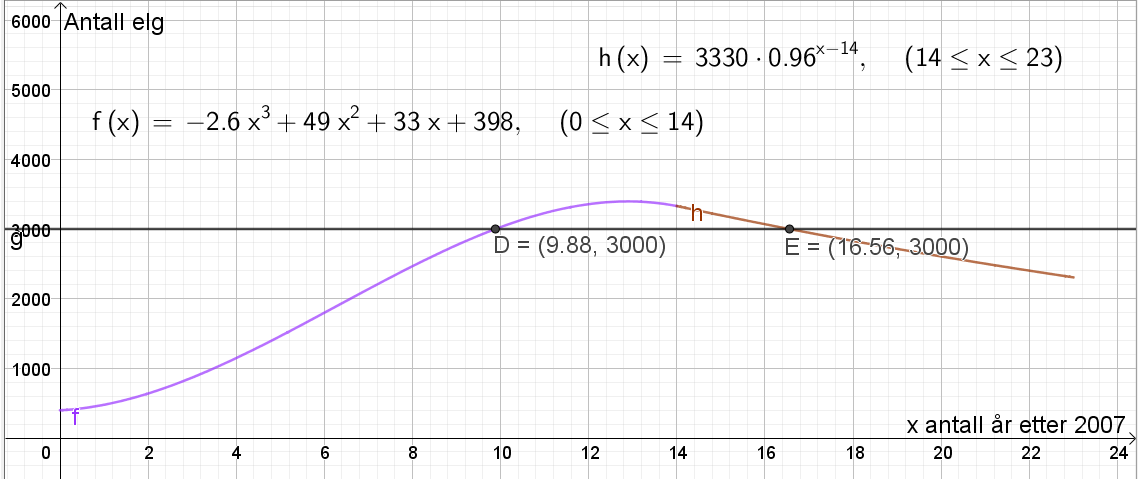
Lager linjen y=3000. Bruker "Skjæring mellom to objekt" for å finne skjæringspunktet mellom linjen y=3000 og henholdsvis grafen til f og grafen til h. Finner punkt D=(9.88, 3000) og E=(16.56, 3000).
Ifølge modellene f og h vil elgbestanden være over 3000 dyr fra 9 til 16 år etter 2007, altså fra år 2016 til år 2023.