S1 2025 Vår LØSNING
Diskusjon av oppgaven på Matteprat
Løsningsforslag laget av Håvard Myge NB: liten regnefeil på oppgave 5b, og dermed også 5c.
Del 1
Oppgave 1
Vi skal derivere funksjonen:
$$ f(x) = e^{-2x} + \frac{1}{5}x^5 - 2\pi $$
Deriver ledd for ledd:
- $e^{-2x} \rightarrow -2e^{-2x}$
- $\frac{1}{5}x^5 \rightarrow x^4$
- $-2\pi \rightarrow 0$, siden $\pi$ er konstant.
Svar: $$ \underline{\underline{f'(x) = -2e^{-2x} + x^4}} $$
Oppgave 2
Funksjonen er gitt som:
$$ g(x) = \frac{1}{2} e^x (2x - 1)^2 $$
a)
Vi setter $g(x) = 0$:
$$ \frac{1}{2} e^x (2x - 1)^2 = 0 $$
Siden $e^x \neq 0$, må:
$$ (2x - 1)^2 = 0 \Rightarrow x = \frac{1}{2} $$
Nullpunkt: $\underline{\underline{x = \frac{1}{2}}}$
b)
La:
- $u(x) = \frac{1}{2} e^x$
- $v(x) = (2x - 1)^2$
Da:
$$ g'(x) = u'(x)v(x) + u(x)v'(x) $$ $$ = \frac{1}{2} e^x (2x - 1)^2 + \frac{1}{2} e^x \cdot 2(2x - 1) \cdot 2 $$
$$ = \frac{1}{2} e^x \left( (2x - 1)^2 + 4(2x - 1) \right) $$
Utvid og faktoriser uttrykket:
$$ (2x - 1)^2 + 4(2x - 1) = (2x - 1)(2x - 1 + 4) = (2x - 1)(2x + 3) $$
Vi har vist at: $$ g'(x) = \frac{1}{2} e^x (2x - 1)(2x + 3) $$
c)
Finn stasjonære punkter ved å løse $g'(x) = 0$:
$$ \frac{1}{2} e^x (2x - 1)(2x + 3) = 0 $$
Løsning: $x = \frac{1}{2}$ og $x = -\frac{3}{2}$
Finn $g(x)$-verdiene:
- $g\left(\frac{1}{2}\right) = \frac{1}{2} e^{1/2} \cdot 0 = 0$
- $g\left(-\frac{3}{2}\right) = \frac{1}{2} e^{-3/2} \cdot (-4)^2 = \frac{1}{2} e^{-3/2} \cdot 16 = 8e^{-3/2}$
Svar:
- Bunnpunkt: $\underline{\underline{\left(\frac{1}{2}, 0\right)}}$
- Toppunkt: $\underline{\underline{\left(-\frac{3}{2}, 8e^{-3/2} \right)}}$
Oppgave 3
a)
$$ 3^{3x + 2} - 5 = 76$$ $$ 3^{3x + 2} = 81 = 3^4 $$ $$ 3x + 2 = 4 $$ $$ \underline{\underline{x = \frac{2}{3}}} $$
b)
$$ 3 \lg x + 2 \lg x^2 + \lg\left(\frac{1}{x^9}\right) = 2 $$
Bruk logaritmeregler:
- $\lg x^2 = 2 \lg x$
- $\lg \left( \frac{1}{x^9} \right) = \lg(1) - \lg(x^9) = -9 \lg x$
Da får vi:
$$ 3 \lg x + 4 \lg x - 9 \lg x = 2 $$ $$ -2 \lg x = 2 $$ $$ \lg x = -1 $$ $$ x = 10^{-1} = \underline{\underline{0,1=\frac{1}{10}}} $$
Oppgave 4
a)
Direkte innsetting gir:
$$ \frac{3(9 - 3)}{0} = \frac{18}{0} $$
Ikke av typen $\frac{0}{0}$ – som betyr at grenseverdien kan gå mot $+\infty$, $-\infty$ eller være udefinert.
Når $x \to 3^-$:
- Telleren nærmer seg $18$ og nevneren er negativ og nærmer seg $0$
- $\Rightarrow$ Brøken går mot $-\infty$
Når $x \to 3^+$:
- Telleren nærmer seg $18$ og nevneren er positiv og nærmer seg $0$
- $\Rightarrow$ Brøken går mot $+\infty$
Grenseverdien eksisterer ikke.
b)
$$ \lim_{x \to 4} \frac{\sqrt{x} - 2}{x - 4} $$
Bruk konjugatsetning med $x-4$: $$ \lim_{x \to 4} \frac{\sqrt{x} - 2}{(\sqrt{x}-2)(\sqrt{ x } + 2)} $$ $$ \lim_{x \to 4} = \frac{1}{\sqrt{x} + 2} $$ $$ =\frac{1}{\sqrt{4} + 2} = \underline{\underline{\frac{1}{4}}} $$
Oppgave 5
a)
Vi antar at det tredje skuddet ikke har skjedd enda.
P(treff på to skudd) = P(treff)*P(treff)
$=0,8 \cdot 0,8 =0,64$
Sannsynligheten for at Arne treffer på de to første skuddene er 0,64.
b)
P(treff på nøyaktig to skudd) = 3*P(treff)*P(treff)*P(ikke treff)
$=3\cdot 0,8 \cdot 0,8 \cdot 0,2 = 0,64\cdot 0,6 =0,384$
Sannsynligheten for at Arne treffer på nøyaktig to av de tre skuddene er 0,384.
c)
P(treff på høyst ett skudd) = P(ikke treff)*P(ikke treff)*P(ikke treff) + 3*P(treff)*P(ikke treff)*P(ikke treff)
$=0,2^3+3\cdot 0,8\cdot 0,2^2 = 0,008+0,096=0,104$
Sannsynligheten for at Arne treffer på høyst ett av de tre skuddene er 0,104.
Oppgave 6
Funksjonene $f$ og $g$ er gitt ved
$$ f(x) = \begin{cases} x^2 + 2, & x < 0 \\ 2e^x, & x \geq 0 \end{cases} $$
og
$$ g(x) = \begin{cases} x^2 + 2, & x < 0 \\ 1, x=0 \\ 2e^x, & x \geq 0 \end{cases} $$
a)
Sjekk om grenser fra venstre og høyre i $x = 0$ gir samme verdi:
- Venstre: $\lim_{x \to 0^-} f(x) = 0^2 + 2 = 2$
- Høyre: $\lim_{x \to 0^+} f(x) = 2e^0 = 2$
Funksjonen $f$ er kontinuerlig i $x = 0$.
b)
Siden $g(0)=1$, og grenseverdiene i oppgave a) var 2, er $g$ ikke kontinuerlig i $x=0$.
DEL 2
Oppgave 1
a)
Med tallene 1,2,3,4,5,6 er det seks mulige tall på hver plass. Det gir $6^3=216$ mulige kombinasjoner.
Sannsynligheten for at Peder klarer å åpne hengelåsen på første forsøk er $\frac{1}{216}=0,00463$
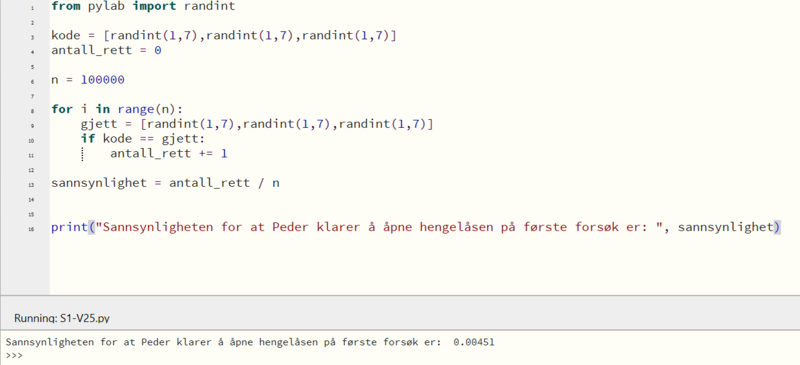
b)
Oppgave 2
Vi bruker navnene $p(x)$, $q(x)$ og $r(x)$ som egendefinerte betegnelser for de tre delene av funksjonen, for å gjøre beregningene tydeligere der
$$ f(x) = \begin{cases} p(x), & x \leq -2 \\ q(x), & -2 < x < 1 \\ r(x), & x \geq 1 \end{cases} $$
$p(x)$ og $r(x)$ er gitt i oppgave, men siden $q$ er et ubestemt tredjegradspolynom kan vi bruke:
$$ q(x) = ax^3 + bx^2 + cx + d $$
- Linje 1-3: Definere $p$, $q$ og $r$ i CAS
Vi ønsker å finne uttrykket for $q(x)$ slik at $f$ er kontinuerlig i hele $\mathbb{R}$. Siden alle $p$, $q$ og $r$ er polynomer, er det bare nødvendig å sjekke i delingspunktene til $f$:
For $x = -2$:
- Kontinuerlig dersom $\lim_{x \to -2^-} f(x) = \lim_{x \to -2^+} f(x) \Rightarrow p(-2) = q(-2)$
- Linje 4: $p(-2) = q(-2)$
- Obs! Selv om $q(-2)$ ikke er definert som funksjonsverdi (siden $q$ bare gjelder for $-2 < x < 1$), kan vi likevel bruke uttrykket $q(-2)$ i CAS for å representere høyre grenseverdi.*
For $x = 1$:
- Kontinuerlig dersom $\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) \Rightarrow q(1) = r(1)$
- Linje 5: $q(1) = r(1)$
Linje 6-7 viser de to verdiene av den deriverte vi får i oppgaveteksten.
Linjer 4–7 utgjør et likningssystem.
- Linje 8: Løsning til likningssystemet:
$$ \begin{aligned} a &= -\frac{13}{27} \\ b &= \frac{7}{9} \\ c &= -\frac{1}{9} \\ d &= -\frac{113}{27} \end{aligned} $$
Det manglende uttrykket i midten av $f(x)$ er:
$$ q(x) = -\frac{13}{27}x^3 + \frac{7}{9}x^2 - \frac{1}{9}x - \frac{113}{27}, \quad \text{for } -2 < x < 1 $$
Oppgave 3
a)
${10 \choose 4}=\frac{10\cdot 9\cdot 8\cdot 7}{4\cdot 3\cdot 2\cdot 1}=210 $
Arbeidsgruppen kan settes sammen på 210 måter.
b)
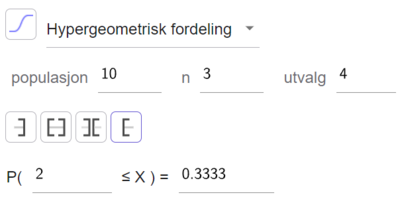
Bruker sannsynlighetskalkulatoren i Geogebra.
Sannsynligheten for at minst to gutter blir med i arbeidsgruppen er ca. 0,333.
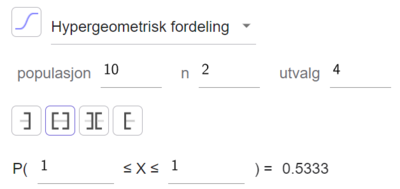
c)
Sannsynligheten for at bare én av jentene blir med i arbeidsgruppen er ca. 0,533.
Oppgave 4
Bruker sannsynlighetskalkulatoren i Geogebra.
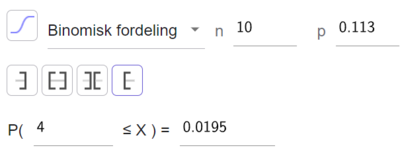
a)
Sannsynligheten for at vi plukker ut minst 4 som stemte på Fremskrittspartiet er 0,0195.
b)
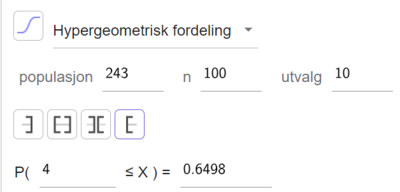
Siden populasjonen er liten, passer ikke binomisk sannsynlighet. Jeg bruker hypergeometrisk sannsynlighet fordi dette er et trekk uten tilbakelegging fra en begrenset populasjon.
Sannsynligheten for at vi plukker ut minst 4 som stemte på Arbeiderpartiet er ca. 0,65.
Oppgave 5
a) og b)
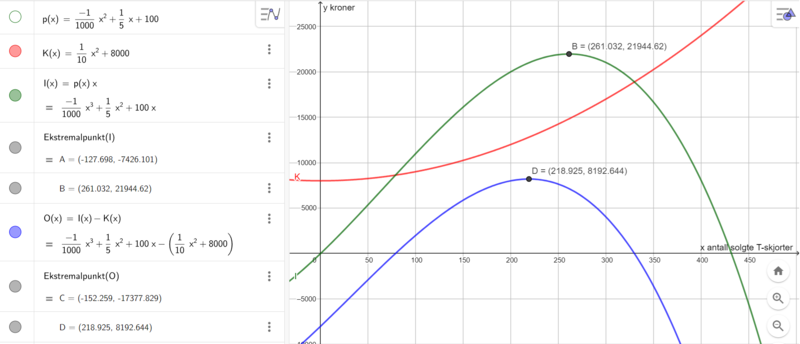
Den største mulige inntekten bedriften kan få per uke er 21944 kr (se punkt B).
Det største mulige overskuddet bedriften kan få per uke er 8193 kr (se punkt D).
c)
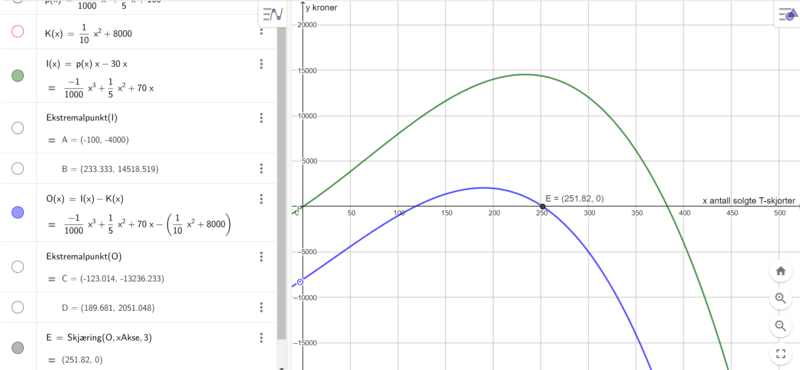
Endrer inntektsfunksjonen ved å legge til -30x (minus 30 kroner per solgte T-skjorte). Finner så nullpunktet til overskuddsfunksjonen som har størst x-verdi.
Bedriften kan selge maksimalt 251 T-skjorter i en uke med kampanje, uten å gå med overskudd. Se punkt E.
Oppgave 6
a)
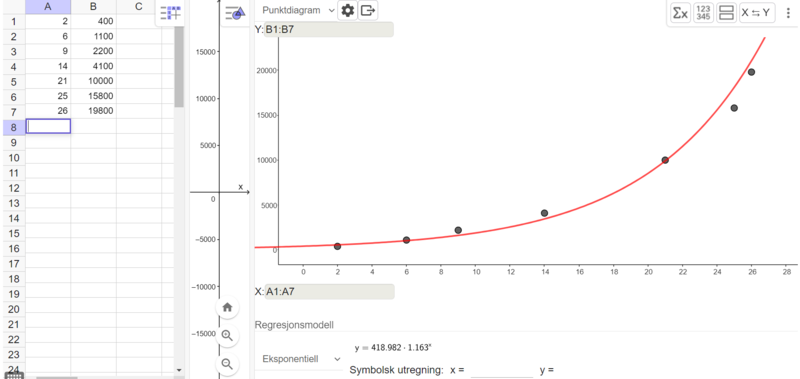
Bruker regresjonsanalyse i Geogebra, med et utvalg av punkter med omtrentlige verdier avlest fra stolpediagrammet. Jeg setter x=0 i år 1998.
Jeg velger en eksponentiell modell, siden den passer godt til dataene, og kun skal være en modell for perioden 1998-2024. Det kan hende modellen passer i en tid fremover, men ikke nødvendigvis.
En modell for utviklingen av den totale verdien av oljefondet i hele perioden kan være $O(t)= 419\cdot 1,163^t$.
b)
Bruker CAS i Geogebra.
$V(20)\approx 8843$. Det betyr at den totale verdien av oljefondet 20 år etter 1998, altså i 2018, er ca. 8843 milliarder kroner, ifølge modellen. Det passer relativt godt med dataene fra stolpediagrammet.
$V'(20)\approx 1454$. Det betyr at i 2018 vokste den totale verdien av oljefondet med ca. 1454 milliarder kroner per år, ifølge modellen.
c)
Den gjennomsnittlige vekstfarten i intervallet [0,10] er ca. 134, som betyr at den totale verdien av oljefondet vokste med ca. 134 milliarder kroner per år fra 1998 til 2008.
Den gjennomsnittlige vekstfarten i intervallet [16,26] er ca. 1913, som betyr at den totale verdien av oljefondet vokste med ca. 1913 milliarder kroner per år fra 2014 til 2024.