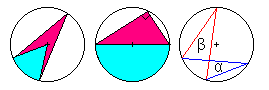Sirkel
En sirkel med senter i <math>(x_0,y_0)</math> er geometrisk definert av alle punkt som har samme avstand, r, fra <math>(x_0,y_0)</math>. Ligningen for en slik sirkel er:
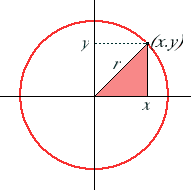
(1) <math> (x - x_0)^2 + (y - y_0)^2 = r^2 </math> Dersom sirkelen har senter i origo, <math>x_0 = y_0 = 0</math>, får vi den enkle sammenhengen:
(2) <math> x^2 + y^2 = r^2 </math> Vi kan forstå denne ligningen ved å betrakte figur 1. Ta et vilkårlig punkt (x,y) som ligger på sirkelen. Trekk en linje fra origo til (x,y). Lengden av denne linjen er, per definisjon, radius r av sirkelen. Vi ser nå fra figuren at punktene (0,0) (x,0) og (x,y) danner en rettvinklet trekant, og videre, at sidene i trekanten er x, y og r der r er hypotenusen. Vi anvender den pytagoreiske læresetning og får <math> x^2 + y^2 = r^2</math>, som er det samme som ligning (2). En sirkel er et kjeglesnitt der kjeglen snittes av et plan normalt til kjeglens symmetriakse.
Formler:
Areal:
<math>A = \pi r^2</math>
Omkrets:
<math> O = 2 \pi r</math>
Begreper
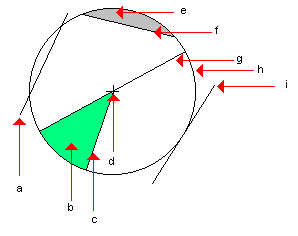
Figuren viser følgende:
a - sekant.
En linje som skjærer sirkelen to steder. Sekanten må ligge i samme plan som sirkelen og har to punkter felles med sirkelen.
b - sirkelsektor
området som begrenses av to radier. Lengden av sektorens sirkelbue er gitt ved s = rθ der θ er vinkelen mellom de avgrensede radiene i absolutte vinkelmål. Arealet av sirkelsektoren er gitt ved <math>A= \frac 12r^2 \theta</math>.
c - radien
sirkelen kan defineres som summe av alle punkter som ligger en gitt avstand fra et punkt P. Denne avstanden fra sentrum til kurven kalles radius og forkortes r.
d - sentrum av sirkelen.
Punkt som angir sirkelens plasering. Punktet har samme avstand til alle steder på sirkelpereferien. Avstanden er r, radius.
e - segment.
En flate som er begrenset av sirkelbuen og en korde som forbinder sirkelbuens endrepunkter. Arealet av et segment er lik arealet av sirkelsektoren minus arealet av trekanten begrenset av korden og radiene. <math>A = \frac 12r^2(\theta - sin{\theta})</math>.
f - korde.
Et rett linjestykke som forbinder to punkter på en kurve (eller plan).
g - diameter.
En korde som går gjennom sirkelens sentrum. Forkortes d eller D. Vi har d = 2r.
h - sirkelperiferien.
Summen av alle punkter som har avstanden r til sentrum.
i - tangent.
En linje som ligger i samme plan som sirkelen og som har et punkt felles med sirkelen. vi sier at linjen tangerer sirkelen.
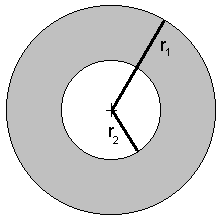
Sirkelring
To konsentriske ( har samme sentrum) sirkler som har forskjellig radius danner en sirkelring Arealet av en sirkelring er arealet av den største sirkelen minus arealet av den minste sirkelen. <math>A = \pi r_1^2 - \pi r_2^2 = \pi (r_1^2 - r_2^2)</math>
Periferi og sentralvinkel
En vinkel med toppunkt på sirkelperiferien kalles en periferivinkel. En vinkel med toppunkt i sentrum kalles en sentralvinkel. En sentralvinkel som spenner over samme buelengde som en periferivinkel vil være dobbel så stor som denne periferivinkelen (periferivinkelsetningen). Alle periferivinkler som spenner over samme buelengde er like store.