Trigonometri II
Absolutt vinkelmål
Radianer (også kalt absolutt vinkelmål) er definert som følger. Ta utgangspunkt i figuren:
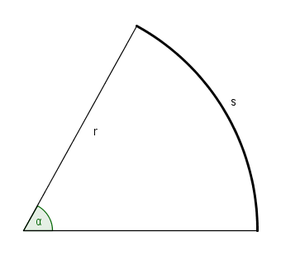
Vi konstruerer en sirkelbue med lengde <math>s</math> og radius <math>r</math>, som vist på figuren. Buen er avgrenset av de to radiene som går fra sentrum av buen. Vinkelen mellom de to radiene i radianer er da definert som
$$\alpha=\frac{s}{r}$$
Det følger at forholdet mellom radianer og grader er gitt ved
\[360^\circ=2\pi \]
eller ekvivalent ved
\[v[^\circ]=\frac{180^\circ}{\pi}v[\text{rad}]\]
for en vinkel $v$
Spisse vinkler
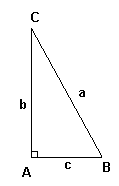
De trigonometriske funksjonene er sinus, cosinus, tangens. Vanligvis forkortes disse sin, cos, tan. For spisse vinkler kan definisjonen av de trigonometriske funksjonene uttrykkes som forholdet mellom sidene i en rettvinklet trekant. Vi har:
DEFINISJONER
• <math>sin B = \frac ba </math>
• <math>cos B = \frac ca </math>
• <math>tan B = \frac bc = \frac{sin B}{ cos B}</math>
Enhetssirkelen
De trigonometriske funksjonene begrenser seg ikke til spisse vinkler.
- Vi tegner en sirkel med radius 1.
- Positive vinkler kan tenkes framkommet ved en dreining mot klokken og negative vinkler fremkommer ved dreining med klokken.
- Dette kalles orienterte vinkler.
- I enhetssirkelen ser vi på orienterte vinkler med absolutte vinkelmål (radianer).
- Dersom en vinkel har høyre vinkelbein sammenfallende med positiv del av x aksen og toppunkt i origo sies vinkelen å være i grunnstilling.
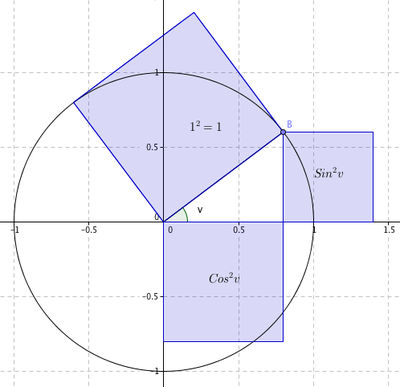
Enhetsirkelen legges med sentrum i origo i et ortonormert koordinatsystem, slik at et av vinkelbeina er sammenfallende med den positive x aksen. Det andre vinkelbeinet skjærer sirkelen i punktet (x,y). De trigonometriske funksjonene defineres som følger:
\[sin (a) = y \quad \quad cos (a) = x \quad \quad tan (a) = \frac yx \]
Sin og cos har begge perioden $2\pi$. Tan har perioden $\pi$.
Enhetssirkelen og dens fire kvadranter:
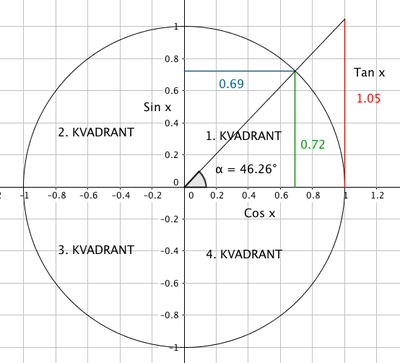
Sinusverdien leses på y aksen (blå) og cosinus på x - aksen grønn.
En geometrosk tolkning av tangens ser du i den røde søylen. Dersom vinkelen ligger i 1. eller 4. kvadrant er lengden av linjestykket fra (1,0) langs linjen normalt på x -aksen, til skjæring med det andre vinkelbeinet. Tillsvarende i ( -1,0) for vinkler i 2. og 3. kvadrant.
Fortegn av trigonometriske funksjoner
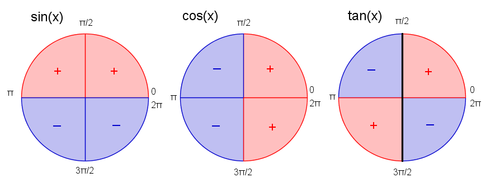
Dette diagrammet viser fortegnene til de forskjellige trigonometriske funksjonene for forskjellige vinkler. Den sorte streken gjennom tangensdiagrammet viser vinklene der <math>\tan\,x</math> går mot <math>\pm\infty</math>. Vi får et bruddpunkt, og det er derfor meningsløst å snakke of fortegnet til <math>\tan\,x</math> når <math>x=\frac{\pi}{2}</math> eller <math>x=\frac{3\pi}{2}</math>.
Hvis du kan disse diagrammene utanat, vil du kunne vurdere hvilke løsninger du forventer til trigonometriske ligninger. Det vil bli lettere å vurdere om løsningene stemmer.
Cosinus
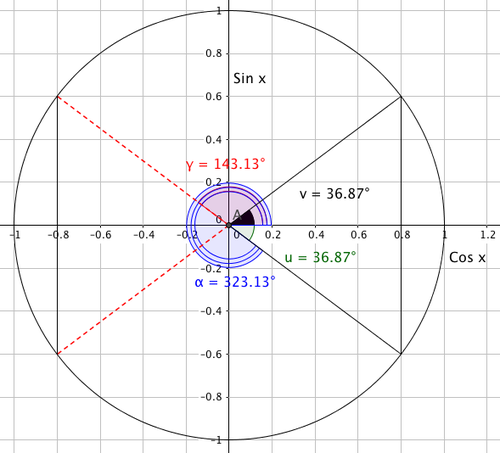
Fra enhetssirkelen ser man blant annet følgende om egenskapene til cosinus:
$v= -u $
$cos (v)= cos(-v) $
$ cos (v) = cos (2 \pi - v) $
$cos v = - cos ( \pi - v)$
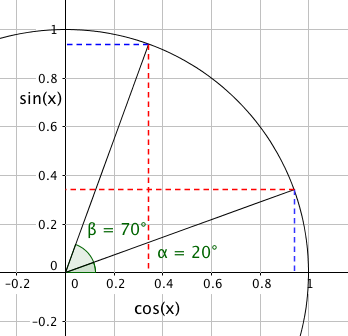
$cos (\alpha) = sin(\frac{\pi}{2}- \alpha) $
$ sin (\alpha) = cos(\frac{\pi}{2} - \alpha)$
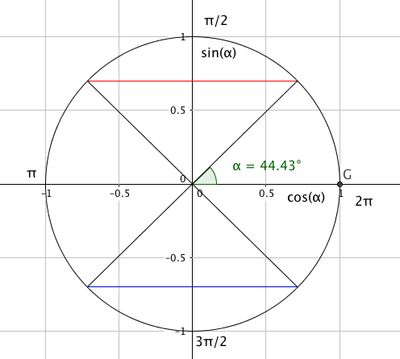
Sinus
Fra enhetssirkelen ser man blant annet følgende om egenskapene til sinus:
$sin( \alpha) = - sin( - \alpha) $
$sin (\alpha) = sin (\pi- \alpha) $
$sin(\alpha) = sin(\alpha +2 \pi) $
$sin( \pi + \alpha)= sin (2\pi -\alpha)$
Når vi plotter sinus- og cosinuskurvene ser de slik ut:
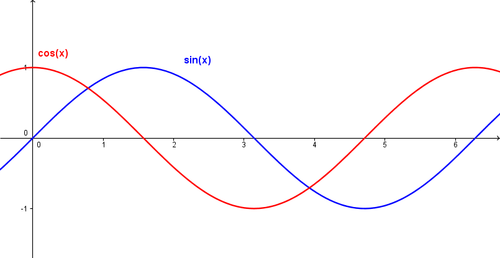
Sinus- og cosinuskurvene har begge perioder på <math>2\pi</math> radianer.
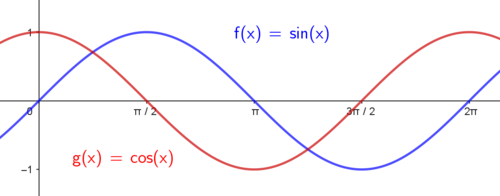
Velg den notasjon på x-aksen du tenker gir best lesbarhet i forhold til oppgaven.
Merk at cosinusfunksjonen kun er sinusfunkjsonen forskjøvet <math>\frac{\pi}{2}</math> radianer i minusretningen. Altså gjelder det at <math>sin(x+\frac{\pi}{2})=\cos\,x</math>
Definisjon av tan(x)
Tangensfunksjonen er definert slik at
- <math>\tan\,x=\frac{\sin\,x}{\cos\,x}</math>
Når vi plotter tangenskurven, ser den slik ut:
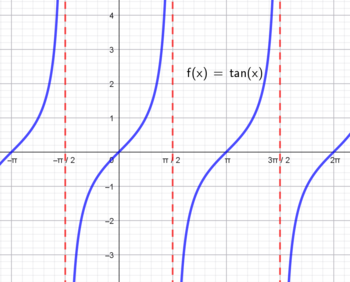
Tangenskurven har en periode på <math>\pi</math> radianer, og den er diskontinuerlig.
Noen viktige verdier av sin x, cos x og tan x på tabellform
Verdiene i tabellen under bør du memorisere. Å kunne disse utenat vil være til stor hjelp i løsingen av trigonometriske ligninger.
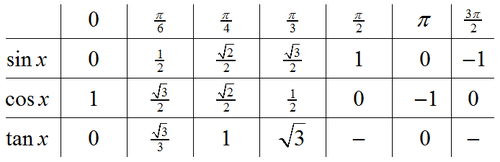
Noen viktige verdier av sin x, cos x og tan x i enhetssirkelen (1. kvadrant)
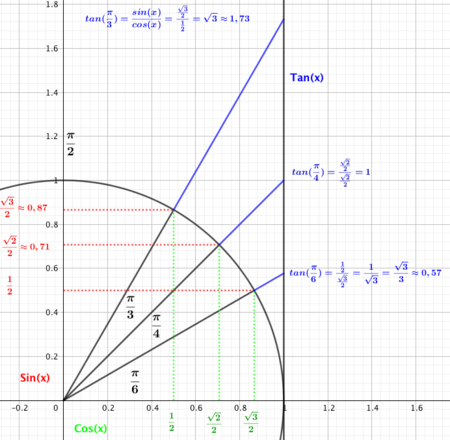
Inverse trigonometriske funksjoner
Vi definerer de inverse trigonometriske funksjonene <math>\arcsin</math>, <math>\arccos</math> og <math>\arctan</math> slik at
- <math>\arcsin(\sin\,x)=x\,,\,x\in [-\frac{\pi}{2},\frac{\pi}{2}]</math>
- <math>\arccos(\cos\,x)=x\,,\,x\in [0,\pi]</math>
- <math>\arctan(\tan\,x)=x\,,\,x\in <-\frac{\pi}{2},\frac{\pi}{2} ></math>
Dersom <math>x</math> ikke befinner seg i disse mengdene, vil du likevel få en verdi innenfor disse mengdene. Ha dette i bakhodet når du løser trigonometriske ligninger på kalkulator.
I mange lærebøker i den videregående skole, og på kalkulatoren er notasjonen slik:
<math>arcsinx = sin^{-1}x\,,\ arccos x = cos^{-1} x \,,\ arctan x = tan^{-1} x</math>
Trigonometriske identiteter
Ettersom alle de trigonometriske funksjonene er periodiske, vil de samme verdiene gå igjen for hver syklus. Generellt gjelder det at
- <math>\sin(x+2\pi)=\sin\,x</math>
- <math>\cos(x+2\pi)=\cos\,x</math>
- <math>\tan(x+\pi)=\tan\,x</math>
Å være klar over disse sammenhengene vil ha betydning når vi senere vurderer løsninger av trigonometriske ligninger.
Ut ifra figuren om definisjonen av sinus og cosinus kan vi se flere egenskaper ved funksjonene. Spesifikt,
- <math>\sin(\pi-x)=\sin\,x</math>
- <math>\sin(-x)=-\sin\,x</math>
- <math>\cos(2\pi-x)=\cos\,x</math>
- <math>\tan(-x)=-\tan\,x</math>
De trigonometriske funksjonene har mange viktige relasjoner med hverandre. Noe som gjelder per definisjon for sinus og cosinus er identiteten
\[sin^2v + cos^2v = 1\quad \quad \color{red}{(1)}\]
.Denne identiteten er viktig fordi den lar oss omforme sinus til cosinus og omvendt.
Sum og differanser av vinkler
\[cos(u-v) = cos(u)\cdot cos(v)+sin(u) \cdot sin(v) \quad \quad \color{red}{(2)}\]
\[\color{black}{cos(u + v) = cos(u)\cdot cos(v)-sin(u)\cdot sin(v)} \quad \quad \color{red}{(3)}\]
\[sin(u - v) = sin(u)\cdot cos(v)-cos(u)\cdot sin(v) \quad \quad \color{red}{(4)} \]
\[sin(u + v) = sin(u)\cdot cos(v)+cos(u)\cdot sin(v)\quad \quad \color{red}{(5)}\]
BEVIS (2):
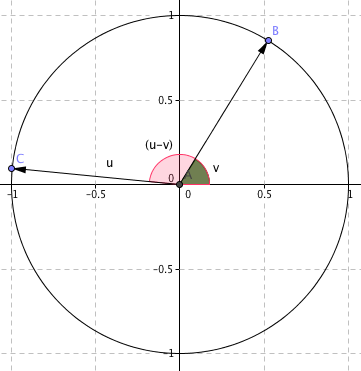
Vinkelen (u-v) er vinkelen mellom vektorene $\vec{OB}$ og $\vec{OC}$ Begge disse har lengde en.
\[\vec{OB}= [\cos v, \sin v] \\ \vec{OC} = [\cos u, \sin u]\]
Skalarprodukt:
\[[\cos u, \sin u] \cdot [\cos v, \sin v] = 1 \cdot 1 \cdot \cos(u-v) \]
\[cos(u-v) = \cos u \cos v + \sin u \sin v \quad \quad \color{red}{(2)}\]
BEVIS (3):
\[\cos(-v)= \cos v \\ \sin(-v) = - \sin v \]
\[\cos(u-v) = \\ \cos(u-(-v)) = \cos u \cos (-v) + \sin u \sin (-v) \]
\[\cos( u+v) = \cos u \cos v - \sin u \sin v \quad \quad \color{red}{(3)} \]
BEVIS (5):
\[ sin v = cos (90 - v) \\ sin (u + v) = cos (90 - (u+v)) \]
\[sin (u+v) = cos ((90-u)-v)\]
\[sin (u+v) = cos (90+u) cosv + sin(90-u)sinv \]
\[sin (u+v) = \sin u \cos v + \cos u \sin v \quad \quad \color{red}{(5)}\]
BEVIS (4):
\[ \sin (u+v)= \sin u \cos v + \cos u \sin v \]
\[ \sin (u+(-v)) = \sin u \cos(-v) + \cos u \sin(-v) \]
\[ \sin (u-v) = \sin u \cos v - \cos u \sin v \quad \quad \color{red}{(4)}\]
Dobble vinkler
\[\sin(2u) = 2sin(u) \cdot cos(u) \quad \quad \color{red}{(6)}\] \[ cos(2u) = cos^2u - sin ^2u \quad \quad \color{red}{(7)}\]
\[\cos(2u) = cos (u+u) \\ = \cos (u) \cos (u) - \sin (u) \sin (u)= \cos^2 (u) - \sin^2 (u) \]
\[cos(2u) = 2 cos^2(u) -1 \quad \quad \color{red}{(8)}\]
\[cos(2u) = 1 - 2 sin^2 (u)\quad \quad \color{red}{(9)}\]
Dersom u + v = 180° har vi at Sin v = sin u og cos v = -cos u
Fra sum til produkt
\[sin u + sin v= 2 sin ( \frac{u+v}{2}) cos ( \frac{u-v}{2})\quad \quad \color{red}{(10)}\]
\[sin u - sin v= 2 cos ( \frac{u+v}{2}) sin ( \frac{u-v}{2})\quad \quad \color{red}{(11)}\]
\[cos u + cos v= 2 cos ( \frac{u+v}{2}) cos ( \frac{u-v}{2})\quad \quad \color{red}{(12)}\]
\[cos u - cos v= - 2 sin ( \frac{u+v}{2}) sin ( \frac{u-v}{2})\quad \quad \color{red}{(13)}\]
Fra produkt til sum
\[sin (u )sin (v) = \frac 12[ cos (u-v) - cos (u+v)]\quad \quad \color{red}{(14)}\]
\[cos (u) cos (v) = \frac 12[ cos (u-v) + cos (u+v)]\quad \quad \color{red}{(15)}\]
\[sin (u) cos (v) = \frac 12[ sin (u+v) + sin (u-v)]\quad \quad \color{red}{(16)}\]
\[cos (u) sin (v) = \frac 12[ sin (u+v) - sin (u-v)]\quad \quad \color{red}{(17)}\]
Trigonometriske likninger
Løsninger og definisjonsmengde
I mange trigonometriske ligninger er definisjonsmengden til variabelen gitt på forhånd. Definisjonsmengden har innflytelse ikke bare på hva løsningene er, men også hvor mange løsninger som finnes. Dersom det ikke er gitt noen definisjonsmengde kan variabelen ha enhver reell verdi. For å få med alle løsninger bruker vi et lite triks, som vi viser nedenfor.
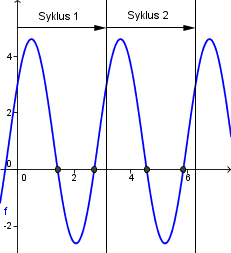
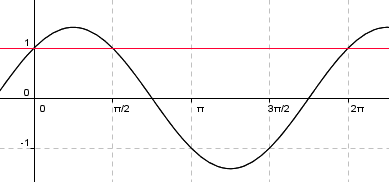
Når definisjonsmengden er gitt, bør du først se om du kan forhåndsbestemme hvor mange løsninger du forventer å få. Gitt at ligningen er løselig er det akseptabelt å forvente to løsninger per <math>2\pi</math>-syklus av de trigonometriske funksjonene. Her er et eksempel:
- Eksempel
- Bildet viser en plott av funksjonen <math>f(x)=3\sin(2x)+2\cos(2x)+1</math>. Nullpunktene til funksjonen, markert med grå prikker, viser løsningene til ligningen <math>3\sin(2x)+2\cos(2x)=-1</math>. Hvis definisjonsmengden er <math>x\in [0,\pi></math>, går funksjonene gjennom én <math>2\pi</math>-syklus, og vi får 2 løsninger. Hvis definisjonsmengden er <math>x\in [0,2\pi></math>, går funksjonene gjennom to <math>2\pi</math>-sykluser, og nå får vi 4 løsninger.
- OBS!
- Regelen om 2 løsninger per syklus gjelder bare hvis vi kan uttrykke ligningen ved én enkelt trigonometrisk funksjon, og denne ikke har sin største eller minste verdi. Som vi skal se senere kan funksjonen over beskrives på formen <math>f(x)=A\sin(x+\phi)+d</math>.
1. Trigonometriske grunnlikninger
Trigonometriske likninger som kun involverer én trigonometrisk funksjon, kaller vi trigonometriske grunnlikninger. Disse er de enkleste trigonometriske likningene å løse, og krever kun kunnskap om de trigonometriske funksjonenes inverser.
Løsningsmetode for trigonometriske grunnlikninger
Vi tar for oss ligningen
\[a\sin(bx)=c\]
Vi vil løse denne ligninger for <math>x</math>. Det første vi gjør er å isolere <math>\sin(bx)</math> på venstresiden:
\[\sin(bx)=\frac ca \]
Siden høyresiden er lik venstresiden, vil <math>\arcsin</math> av høyresiden være lik <math>\arcsin</math> av venstresiden. Altså:
\[ \arcsin(\sin(bx))=\arcsin(\frac ca) \]
Dette gir oss to uttrykk for <math>x</math>:
\[ bx=\arcsin(\frac ca)\, \quad \vee \quad \,\pi-bx=\arcsin(\frac ca)\]
Sinus er periodisk i <math>2\pi</math> så vi må legge til en vilkårlig multippel av <math>2\pi</math> på hver side.
\[bx+k\cdot2\pi=\arcsin(\frac ca)\, \quad \vee \quad \,\pi-bx+k\cdot2\pi=\arcsin(\frac ca)\,,\,k\in\mathbb{Z}\]
- Når vi isolerer <math>x</math> på venstresiden får vi
\[x=\frac{\arcsin(\frac ca)-k\cdot2\pi}{b}\, \quad \vee \quad \,x=\frac{\pi(2k+1) -\arcsin(\frac ca)}{b}\,,\,k\in\mathbb{Z}\]
Den samme fremgangsmåten kan benyttes på trigonometriske grunnlikninger med <math>\cos</math> og <math>\tan</math> også, men husk at disse har litt forskjellige egenskaper, så løsningene blir ikke de samme.
EKSEMPEL 1.
$2cos(\pi x)=1 \quad \quad \quad x\in [0, 2\pi>$
$ cos( \pi x) = \frac 12 \\$
$\pi x = \frac{\pi}{3} +k2\pi \vee \pi x = 2\pi-\frac{\pi}{3} + k2\pi$
$x= \frac 13+2k \vee x=2- \frac13 +2k $
$\\ x= \frac 13 \vee x= \frac 73 \vee x= \frac{13}{3} \vee x= \frac 53 \vee x= \frac{11}{3} \vee x= \frac{17}{3}$
$x \in${$ \frac{1}{3}, \frac{5}{3}, \frac{7}{3}, \frac{11}{3}, \frac{13}{3}, \frac{17}{3}$}
Slik ser det ut:
SIN
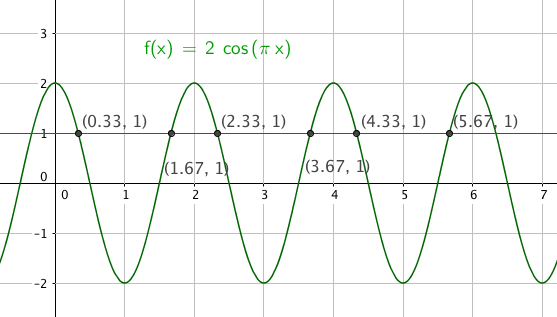
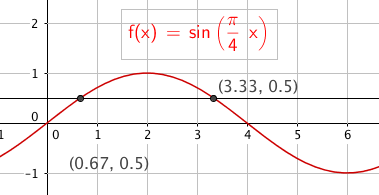
$sin( \frac{\pi}{4}x) = \frac 12 \quad \quad \quad x \in[0, 2 \pi> \\$
$\frac{\pi}{4}x = \frac{\pi}{6} +2k \pi \vee \frac{\pi}{4}x = \pi - \frac{\pi}{6} +2k \pi \\$
$x= \frac 23 +8k \vee x = 4- \frac 23 + 8k $
$\\ x= \frac 23 \vee x = \frac{10}{3}$
$x \in ${$ \frac 23, \frac{10}{3}$}
Slik ser det ut:
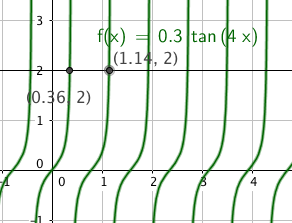
TAN
$0,3 tan(4x)= 2 \quad \quad \quad x \in [0, \frac{\pi}{2}> $
$tan(4x) = 6,667$
$ 4x = 1,42 + k \pi$
$ x= 0,36 \vee x= 1,14$
$x \in ${ 0,36 , 1,14}
Slik ser det ut:
2 \[a cos^2 x + b cos x + c = 0\] eller \[ a sin^2 x + b sin x + c = 0\]
Løses ved å erstatt cos x , eventuelt sin x, med u. Løser andregradsligningen og setter løsningen(e) lik cos x (eller sin x ) og finner mulige x verdier.
Eksempel 2.
<math>\sin^2x+\sin\,x-1=0\,,\,x\in[0,2\pi></math>
Setter sin x = u og bruker andregradsformelen, og får:
<math>\sin\,x=\frac{\sqrt{5}-1}{2}</math>
<math>\sin\,x=\frac{\sqrt{5}+1}{2}</math>
Merk at <math>\frac{\sqrt{5}+1}{2}>1</math>, altså har ikke denne grunnlikningen noen løsninger.
Vi står igjen med kun den første trigonometriske grunnlikningen. Når vi løser denne, får vi
$x= 0,67 \vee x= 2,48$
Slik ser det ut:
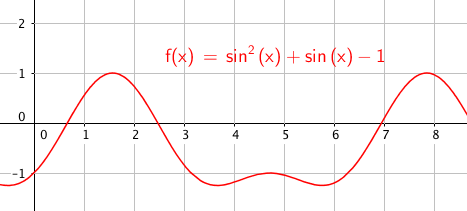
$x \in${0,67 , 2,48}
3
\[a sin x + b cos x = 0\]Begge sider divideres med cos x (forskjellig fra null). Vi får da en identitet i tan x.
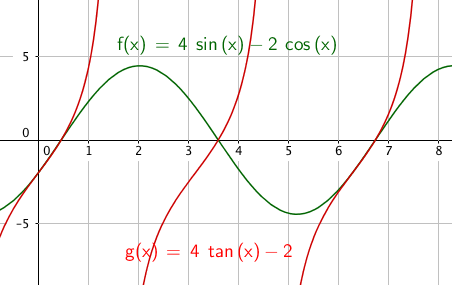
Eksempel 3
\[4sinx-2cosx=0 \quad \quad x \in [0, 2 \pi> \]
\[ 4tanx-2=0 \]
\[tanx = \frac 12 \]
\[ x = tan^{-1}(\frac 12) = 0,46 + k \pi \]
\[ x= 0,46 \vee x = 3,61\]
\[x \in \{0,46 , \quad 3,61\} \]
Slik ser det ut:
4
Ligningen løses ved å erstatte $sin^2x \quad $ med $1 - cos^2 x \quad$ eller $ cos^2 x \quad$ med $1 - sin^2 x$
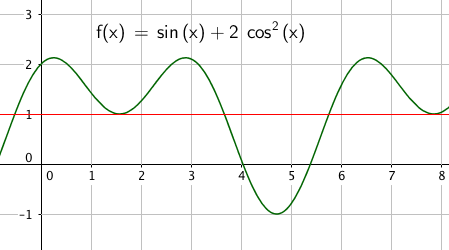
Eksempel 4:
- <math>\sin\,x+2cos^2x=1\,,\,x\in[0,2\pi > </math>
- Vi kjenner identiteten <math>\sin^2x+\cos^2x=1</math>.
Den kan vi bruke her for å omforme ligningen til
- <math>\sin\,x+2-2\sin^2x=1</math>
- <math>2\sin^2x-\sin\,x-1=0</math>
- Dette er en andregradslikning i $\sin\,x$, som vi kan løse:
- <math>\sin\,x=\frac{1\pm\sqrt{1+8}}{4}=\frac{1\pm 3}{4}</math>
- <math>\sin\,x=\frac{1+3}{4}=1 \,\vee\,\sin\,x=\frac{1-3}{4}=-\frac12</math>
- <math>\sin\,x=1\,\Rightarrow\,x=\frac{\pi}{2}</math>
- <math>\sin\,x=-\frac12\,\Rightarrow\,x=\frac{7\pi}{6} \,\vee\,x=\frac{11\pi}{6}</math>
$x= \frac {\pi}{2} \vee x= \frac{7 \pi}{6} \vee x= \frac{11 \pi}{6}$
$x \in${$\frac {\pi}{2}, \frac{7 \pi}{6}, \frac{11 \pi}{6}$}
Slik ser det ut:
5
\[a sin^2 x + b sin x cos x + c cos^2 x = 0\]Løses ved å dividere begge sider av likhetstegnet med $cos^2 x \quad \quad cos x \neq 0$
Eksempel 5:
\[2sin^2x+3sinxcosx - cos^2x=0 \quad x \in [0, 2\pi> \]
\[ 2tan^2x+3tanx-1=0 \] \[ 2u^2+3u-1=0\]
\[tan x =-1,06 \vee tanx = 0,27 \]
\[x= -1,06 + k\pi \vee x= 0,27 + k\pi \]
\[x = 0,27 \vee x=3,45 \vee x=2,08 \vee x=5,22 \]
\[x \in$ {0,27 , 2,08 , 3,45 , 5,22}\]
Slik ser det ut:
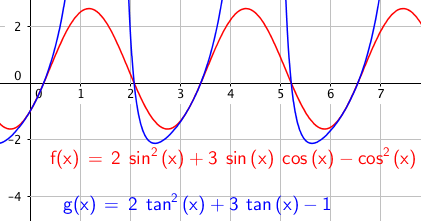
6 \[ a sin^2 x + b sin x cos x + c cos^2 x = d \]
Her må konstantleddet skrives om : $d = d \cdot 1 =d(sin^2 x + cos^2 x)$ . Ligningen løses nå som beskrevet i punktet over.
Eksempel 6:
\[4sin^2x+ sinx cos x - 3cos^2x=3 \quad \quad x \in [0, 2\pi> \]
\[4sin^2x+ sinx cos x - 3cos^2x = 3sin^2x + 3cos^2x \]
\[ \ sin^2x + sinx cosx - 6cos^2 = 0 \]
\[ \ tan^2x + tanx - 6 = 0 \\ tanx = -3 \vee tanx = 2 \]
\[ x= -1,24 +k\pi \vee x=1,11 + k\pi \]
\[ x= 1,11 \vee x= 4,25 \vee x= 1,90 \vee x=5,04 \]
\[x \in ${1,11 , 1,90 , 4,25 , 5,04} \]
Slik ser det ut:
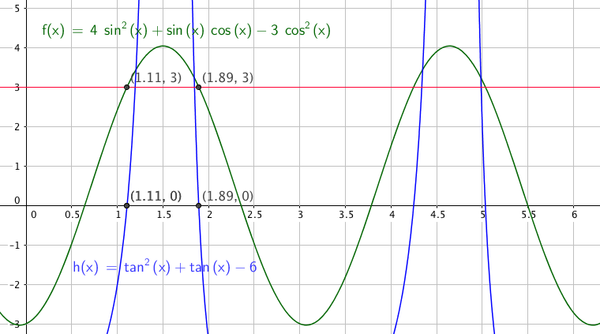
7
Likninger av typen \[ a\sin cx + bcos cx = d \] Løses ved å skrive om til:\[ Asin (cx + \varphi)=d \] der \[A=\sqrt{a^2+b^2} \] og <math>\varphi</math> er gitt ved <math> tan \varphi = \frac ba</math> og <math>\varphi</math>ligger i samme kvadrant som (a,b).
- Eksempel 7:
Vinkelen <math>\varphi</math> ligger i første kvadrant, <math>\varphi =tan^{-1}(1)= \frac {\pi}{4} </math>
Vi får$\sqrt 2 sin(x + \frac \pi 4) = 1 \\ sin (x+ \frac \pi 4) = \frac{\sqrt 2}{2} \\ x + \frac {\pi}{4} = \frac {\pi}{4} +2k\pi \vee x + \frac{\pi}{4}= \pi - \frac{\pi}{4} +2k\pi \\ x=0 \vee x= \frac {\pi}{2}$
$x \in$ {0, $\frac \pi 2$}
Det ser slik ut:
8
\[a^2\pm ab= 0 \Rightarrow a( a \pm b)= 0\]
a og b er sinx og cosx, eller cosx og sinx.
Eksempel 8
Når vi skal løse trigonometriske ligninger må vi ofte dele den opp i flere trigonometriske grunnlikninger før vi kan løse den. Et klassisk eksempel er faktoriseringsmetoden. Vi tar for oss ligningen
<math>\sin\,x\,\cos\,x-cos\,x=0\,,\,x\in [0,2\pi></math>
Selv om det kan være fristende, må du, uansett hva du gjør, ikke dele på <math>\cos\,x</math>. Generelt prøver man å ikke dele eller multiplisere med funksjoner av variabler, fordi du kan miste løsninger, eller lage falske løsninger. Dette gjelder generelt når du deler på null eller multipliserer med null. I stedet faktoriserer vi ligningen:
<math>\cos\,x\,(\sin\,x-1)=0</math>
- Nå ser vi at for at ligningen skal oppfylles, må <math>\cos\,x=0</math> eller <math>\sin\,x-1=0</math>. Vi har klart å redusere den kompositte trigonometriske ligningen til to trigonometriske grunnlikninger.
- <math>\sin\,x=1 \,\Rightarrow\, x=\frac{\pi}{2}</math>
- <math>\cos\,x=0 \,\Rightarrow\, x=\frac{\pi}{2} \,\vee\, x=\frac{3\pi}{2}</math>
$ x \in${$\frac{\pi}{2} , \frac{3\pi}{2}$}
- NB: Dersom du på forhånd har sjekket at det du deler eller multipliserer med ikke er lik null, er det greit å gjennomføre operasjonen. Dette kan gjøres ved å plugge inn null for den aktuelle faktoren og se om likningen oppfylles.
Funksjoner og drøfting
Nullpunkt
For å finne nullpunktene til trigonometriske funksjoner må man kunne løse likninger, fordi man som vanlig setter $f(x)=0$ og løser for x.
Ekstremalpunkt for Sinus og Cosinus
Man kan derivere funksjonen og sette den deriverte lik null, men ofte er det lettere å benytte egenskapene til sinus og cosinus funksjonene.
Vi vet at de antar verdier fra -1 til 1.
Vi har funksjonen $g(x) = 3sin(2x- \frac{\pi}{4})-1 \quad D_g= [0, 3 \pi>$
Finn maksimumspunktene til g.
Vi vet funksjonen har sin (u) maksimale verdi lik 1 når $u= \frac {\pi}{2}$
$2x- \frac{\pi}{4} = \frac {\pi}{2}$
Så må vi ta hensyn til at definisjonsmengden går fra 0 til $3 \pi$ og får:
\[2x- \frac{\pi}{4} = \frac {\pi}{2} + 2 \pi k \]
\[8x - \pi = 2 \pi + 8k \pi \]
\[x = \frac{3 \pi}{8} +k \pi \] \[k=0 \, gir \, x=\frac{3 \pi}{8} \]
\[k=1 \, gir \, x=\frac{11 \pi}{8} \] \[k=2 \, gir \, x=\frac{19 \pi}{8}\]
k = 3 kommer over øvre grensen til definisjonsmengden, og skal ikke være med.
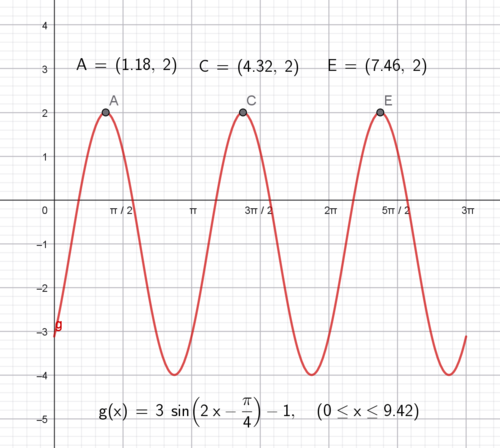
Alternativt kan man derivere g og løse g'(x) = 0
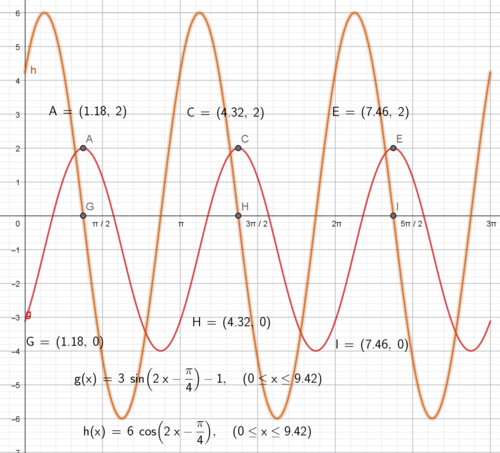
h(x) = g'(x)
Harmoniske svingninger
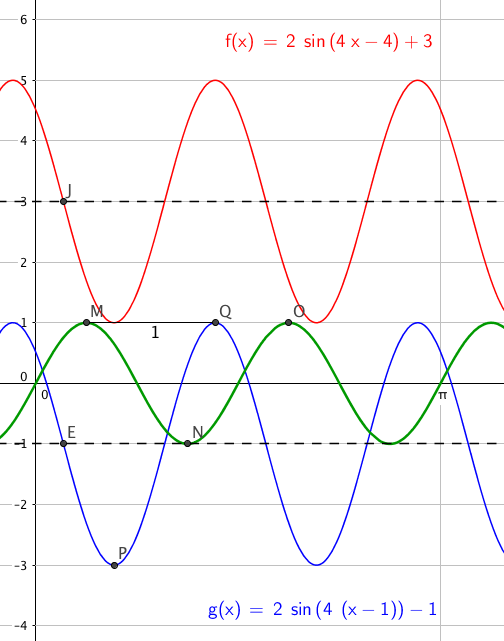
Generellt ser uttrykket til en sinusfunksjon slik ut:
$f(x) = A sin(kx+c) + d$
Hvordan kan vi knytte dette funksjonsuttrykket sammen med en graf som ser slik ut?:
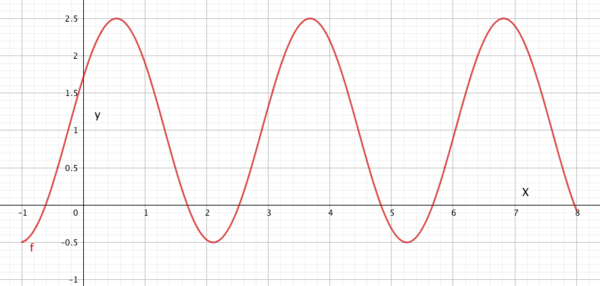
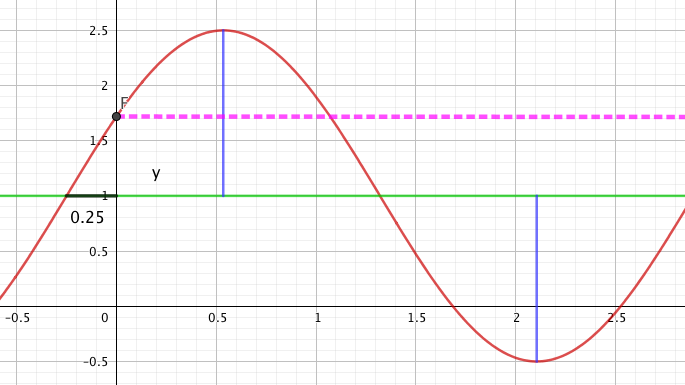
Likevektslinje
Likevektslinjen er den linjen den periodiske funksjonen svinger rundt. Utslaget er like stort til begge sider (opp og ned).
Likevektslinje: y = d
Vi finner uttrykket for d ved å regne ut: $d= \frac{f_{maks}+ f_{min}}{2}= \frac{2,5+(-0,5)}{2} = 1$
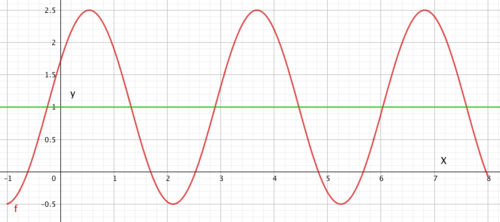
Amplitude: A
Amplituden er det største utslaget på grafen. Når du skrur på volumet på stereoen din bestemmer du amplituden. Dersom du ønsker høy lyd er aplituden stor..
Amplituden er utslaget fra likevekstlinja, og er alltid positivt.
Amplitude: $\quad f_{max}- d = 2,5-1 = 1,5 $
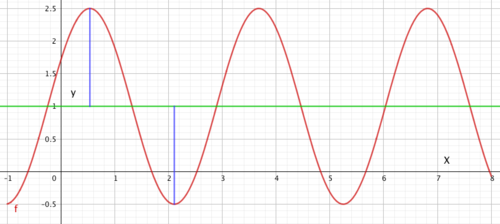
Man må merke seg at amplituden er en absoluttverdi, den er alltid positiv fordi den måler avstanden fra likevekstlinje til maksimalt (eller minimalt) utslag.
Amplituden er lengden av den blå linjen. Den grønne linjen er likevekstlinjen.
Da har vi etablert at modellen ser slik ut: $f(x)=1,5 sin(kx+c) +1$
Vi mangler fortsatt k og c.
Periode
Hvor mange ganger funksjonen repeterer seg selv i intervallet $2 \pi$ multiplisert med lengden av repetisjonen gir:
$pk = 2 \pi$
Peiode P: $ p = \frac {2 \pi}{k} , \quad \quad \quad \quad Antall \, repetisjoner\, i \ 2\pi: k= \frac{2\pi}{p}$
k er gjentakelser i intervallet $2 \pi$ og p er lengden av perioden.
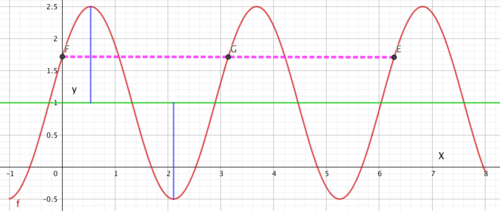
Den stiplede linjen viser gjentakelsene av funksjonen en fra F til G, og en fra G til E, altså k = 2.
k er antallet ganger funksjonen repeterer seg selv i intevallet $2 \pi$. Fra figuren ser man at k = 2 og at lengden på peroden blir $\pi$
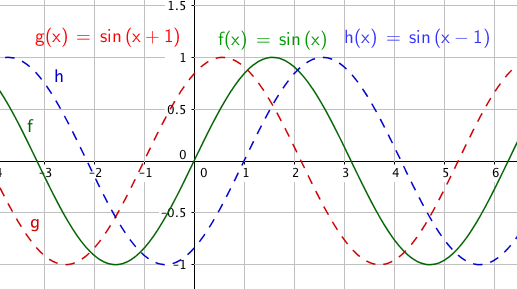
Faseforskyvning
sin (x) og sin (kx) vil være null for x = 0, for så å vokse med økende x. Ved faseforskyvning blir grafen forskjøvet.
Vi finner skjæring med likevektslinje ved å sette
kx + c= 0
Faseforskyvning: $\quad x =- \frac{c}{k}$
Man observere at faseforskyvningen er -0,25. Vi tar utgangspunkt i punktet der likevektslinjen krysser y aksen og beveger oss til den delen av grafen som vokser, fordi sinusfunksjonen vokser for vinkler i første kvadrant. Se fuguren over.
Da blir c: $ kx +c =0 \Rightarrow c= - kx \Rightarrow c= -2 \cdot(- \frac14) = \frac 12$
Dersom $c<0$ forskyves grafen mot høyre.
Dersom $c> 0$ forskyves grafen mot venstre.
Funksjonsutrykket ser slik ut: $f(x)= \frac 32sin(2x+ \frac{1}{2}) +1$
Dersom vi faktoriserer uttrykket man skal ta sinus av får man
$f(x)= \frac 32 sin(2(x + \frac 14)) +1$
Her ser man at faseforskyvningen vises eksplisit.
Litt mere om faseforskyvning
Alternativ skrivemåte
Fra Sin og Cos til Sin
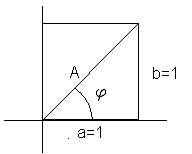
Vi ønsker å skrive funksjonen $f(x)= a sin cx + b cos cx$ på formen $g(x)= A sin (cx +\varphi)$. Sin og Cos har samme periode.
Vi tar utgangspunkt i en harmonisk svingning med x-aksen som likevektslinje (d = 0).:
\[A Sin(kx + \varphi)\]
Formelen for sinus til summen av to vinkler¤ gir:
\[A Sin (kx+ \varphi) = A(Sin(kx) Cos (\varphi) + Cos (kx) Sin (\varphi)) \] \[A Sin (kx+ \varphi) = A Cos (\varphi) Sin(kx) + A Sin (\varphi) Cos(kx)) \] \[A Sin (kx+ \varphi) = a Sin(kx) + bCos(kx)) \]
der $ a=A Cos (\varphi)$ og $ b=A Sin (\varphi)$
a og b kjenner vi, fordi de inngår i det uttrykket vi skal omforme.
Det er to ukjente, A og $\varphi $
Finner A:
\[ \sqrt{a^2+b^2} = \sqrt{(A Cos(\varphi))^2 + (A Sin(\varphi))^2} \]
\[ \sqrt{a^2+b^2} = \sqrt{A^2( Cos^2(\varphi) + Sin^2(\varphi))} \] \[ \sqrt{a^2+b^2} = \sqrt{A^2 \cdot 1} \] \[ \sqrt{a^2+b^2} = A \]
Finner $\varphi$: \[\frac{ASin\varphi}{ACos \varphi} = \frac{b}{a} = tan \varphi \]
Bruker den løsningen som ligger i samme kvadrant som punktet (a,b).
Altså: a sin cx + b cos cx = A sin (cx + $\varphi$)
$A = \sqrt{a^2 + b^2}$ og $tan \varphi = \frac ba$
NB: $\varphi$ ligger i samme kvadrant som punktet (a, b)
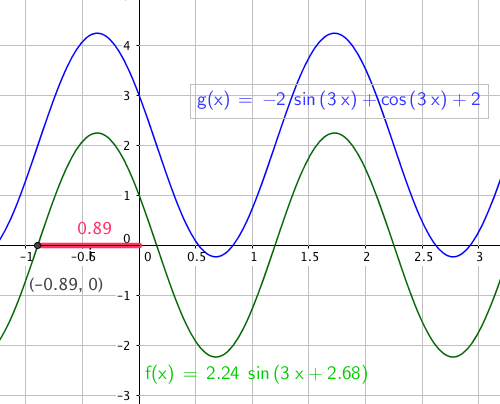
Eksempel:
f(x) = -2 sin 3x + cos 3x $\quad \quad A= \sqrt{(-2)^2 + 1^2} = \sqrt 5 = 2,24 \quad \quad tan \varphi = - \frac 12 \Rightarrow \varphi = 2,678$
Husk at punktet (-2,1) ligger i andre kvadrant, så vi jakter på en vinkel i denne kvadranten.
Vi får : f(x)= 2,24 sin(3x + 2,,678)
Her er utgangsfunksjonen, her kalt g(x) tegnet med likevektslinje y = 2, bare for å kunne sammenligne grafene til de to uttrykkene. Vi ser at de er identiske, med en faseforskyvning mot venstre på $ \frac{2,678}{3} = 0,89$.
Derivasjon av trigonometriske funksjoner
I denne seksjonen finner du beviser for formlene for derivasjon av de trigonometriske funksjonene.
- Derivasjon av sin x
\[\frac{d}{dx}\sin\,x=\lim_{\Delta x\to0}\frac{\sin(x+\Delta x)-\sin\,x}{\Delta x}\]
- Vi bruker sumformelen for sinus og ekspanderer den venstre sinusfunksjonen.
\[ \lim_{\Delta x\to0}\frac{\sin\,x\,\cos\,\Delta x + \cos\,x\,\sin\,\Delta x-\sin\,x}{\Delta x}\]
- Vi faktoriserer:
\[\lim_{\Delta x\to0}\frac{\sin\,x\,\left(\cos\,\Delta x-1\right) + \cos\,x\,\sin\,\Delta x}{\Delta x}\]
- Vi har nå en sum av to genseverdier:
\[\lim_{\Delta x\to0}\sin\,x\frac{\cos\,\Delta x-1}{\Delta x} + \cos\,x\frac{\sin\,\Delta x}{\Delta x}\]
- Det kan bevises geometrisk at
\[\lim_{\Delta x\to0}\frac{\cos\,\Delta x-1}{\Delta x}=0\]
- og at
\[\lim_{\Delta x\to0}\frac{\sin\,\Delta x}{\Delta x}=1\]
- Resultatet blir da at
\[\frac{d}{dx}\sin\,x=\cos\,x\]
\[(Sin(x))' = Cos(x)\]
- Derivasjon av cos x
- <math>\frac{d}{dx}\cos\,x=\lim_{\Delta x\to0}\frac{\cos(x+\Delta x)-\cos\,x}{\Delta x}</math>
- Vi bruker sumformelen og ekspanderer den venstre cosinusfunksjonen.
- <math>\lim_{\Delta x\to0}\frac{\cos\,x\,\cos\,\Delta x-\sin\,x\,\sin\,\Delta x-\cos\,x}{\Delta x}</math>
- Vi faktoriserer.
- <math>\lim_{\Delta x\to0}\frac{\cos\,x\,\left(\cos\,\Delta x-1\right)-\sin\,x\,\sin\,\Delta x}{\Delta x}</math>
- Vi har nå en sum av to grenseverdier:
- <math>\lim_{\Delta x\to0}\cos\,x\frac{\cos\,\Delta x-1}{\Delta x}-\sin\,x\frac{\sin\,\Delta x}{\Delta x}</math>
- Disse grenseverdiene er de samme som vi støtte på i beviset av derivasjonen av sinusfunksjonen. Dermed blir resultatet at
- <math>\frac{d}{dx}\cos\,x=-\sin\,x</math>
\[(Cos(x))' = -Sin(x)\]
- Derivasjon av tan x
- Nå som vi har derivasjonsformlene for sinus og cosinusfunksjonene, kan vi derivere tangensfunksjonen. Til det bruker vi definisjonen av tangens og skriver den som en brøk av sinus og cosinus og bruker brøkregelen.
- <math>\frac{d}{dx}\tan\,x=\frac{d}{dx}\frac{\sin\,x}{\cos\,x}=\frac{\left(\frac{d}{dx}\sin\,x\right)\cos\,x-\left(\frac{d}{dx}\cos\,x\right)\sin\,x}{\cos^2x}=\frac{\cos^2x+\sin^2x}{\cos^2x}</math>
- Vi nevnte i seksjonen om trigonometriske identiteter at vi skulle bevise identiteten om tangens og cosinus. Det gjør vi nå. Det er to måter å forenkle brøken over på. Den ene er å trekke sammen sinus og cosinus med <math>\sin^2x+\cos^2x=1</math>. Den andre er å separere brøken.
- <math>\frac{\cos^2x+\sin^2x}{\cos^2x}=\frac{1}{\cos^2x}</math>
- <math>\frac{\cos^2x+\sin^2x}{\cos^2x}=\frac{\sin^2x}{\cos^2x}+\frac{\cos^2x}{\cos^2x}=\tan^2x+1</math>
- Ettersom disse uttrykkene åpenbart må være like, har vi bevist identiteten.
- Resultatet av derivasjonen er
- <math>\frac{d}{dx}\tan\,x=\tan^2x+1</math>
- og
- <math>\frac{d}{dx}\tan\,x=\frac{1}{\cos^2x}</math>
\[(tan(x))' = tan^2(x) + 1 = \frac{1}{Cos^2(x)}\]
Flere funksjoner
De tre funksjonene som følger er ikke pensum i R2.
De tre neste er ikke pensum, men greie å kjenne til:
• <math>cot B = \frac cb = \frac{ cos B}{sin B} = \frac {1}{tan B}</math>
• <math>sec B = \frac ac = \frac{1}{cos B}</math>
• <math>cosec B = \frac ab = \frac{1}{sin B} </math>
\[tan^2v + 1 = sec^2v\quad \quad\quad \quad \color{red}{(2)} \]
\[ cot^2v+1 = csc^2v\quad \quad \color{red}{(3)}\]
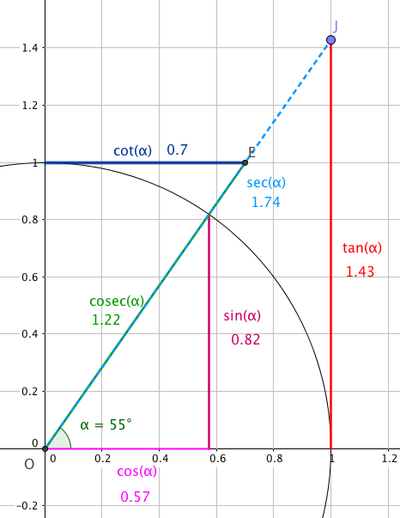
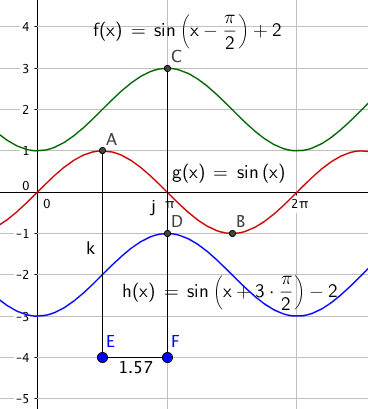
Geometrisk tolkning av de trigonometriske funksjonene. Figuren nedenfor viser de forskjellige trigonometriske funksjonene inntegnet i enhetssirkelen.
| Uttrykt ved | <math> \sin v\!</math> | <math> \cos v\!</math> | <math> \tan v!</math> | <math> \csc v\!</math> | <math> \sec v\!</math> | <math> \cot v\!</math> |
|---|---|---|---|---|---|---|
| <math> \sin v =\!</math> | <math> \sin v \! </math> | <math>\pm\sqrt{1 - \cos^2 v}\! </math> | <math>\pm\frac{\tan v}{\sqrt{1 + \tan^2 v}}\! </math> | <math> \frac{1}{\csc v}\! </math> | <math>\pm\frac{\sqrt{\sec^2 v - 1}}{\sec v}\! </math> | <math>\pm\frac{1}{\sqrt{1 + \cot^2 v}}\! </math> |
| <math> \cos v =\!</math> | <math>\pm\sqrt{1 - \sin^2 v}\! </math> | <math> \cos v\! </math> | <math>\pm\frac{1}{\sqrt{1 + \tan^2 v}}\! </math> | <math>\pm\frac{\sqrt{\csc^2 v - 1}}{\csc v}\! </math> | <math> \frac{1}{\sec v}\! </math> | <math>\pm\frac{\cot v}{\sqrt{1 + \cot^2 v}}\! </math> |
| <math> \tan v =\!</math> | <math>\pm\frac{\sin v}{\sqrt{1 - \sin^2 v}}\! </math> | <math>\pm\frac{\sqrt{1 - \cos^2 v}}{\cos v}\! </math> | <math> \tan v\! </math> | <math>\pm\frac{1}{\sqrt{\csc^2 v - 1}}\! </math> | <math>\pm\sqrt{\sec^2 v - 1}\! </math> | <math> \frac{1}{\cot v}\! </math> |
| <math> \csc v =\!</math> | <math> \frac{1}{\sin v}\! </math> | <math>\pm\frac{1}{\sqrt{1 - \cos^2 v}}\! </math> | <math>\pm\frac{\sqrt{1 + \tan^2 v}}{\tan v}\! </math> | <math> \csc v\! </math> | <math>\pm\frac{\sec v}{\sqrt{\sec^2 v - 1}}\! </math> | <math>\pm\sqrt{1 + \cot^2 v}\! </math> |
| <math> \sec v =\!</math> | <math>\pm\frac{1}{\sqrt{1 - \sin^2 v}}\! </math> |
<math> \frac{1}{\cos v}\! </math> | <math>\pm\sqrt{1 + \tan^2 v}\! </math> | <math>\pm\frac{\csc v}{\sqrt{\csc^2 v - 1}}\! </math> | <math> \sec v\! </math> | <math>\pm\frac{\sqrt{1 + \cot^2 v}}{\cot v}\! </math> |
| <math> \cot v =\!</math> | <math>\pm\frac{\sqrt{1 - \sin^2 v}}{\sin v}\! </math> | <math>\pm\frac{\cos v}{\sqrt{1 - \cos^2 v}}\! </math> | <math> \frac{1}{\tan v}\! </math> | <math>\pm\sqrt{\csc^2 v - 1}\! </math> | <math>\pm\frac{1}{\sqrt{\sec^2 v - 1}}\! </math> | <math> \cot v\! </math> |
Ved observasjon ser vi at fortegnet til en trigonometrisk funksjon varierer avhengig av hvilken kvadrant man befinner seg i. Nedenfor følger en oversikt.
| Kvadrant | I | II | III | IV |
| cos | pos | neg | neg | pos |
| sin | pos | pos | neg | neg |
| tan | pos | neg | pos | neg |
| cot | pos | neg | pos | neg |
| sec | pos | neg | neg | pos |
| cosec | pos | pos | neg | neg |