R2 2010 vår LØSNING: Forskjell mellom sideversjoner
| (41 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 5: | Linje 5: | ||
=== a) === | === a) === | ||
$f(x)=x^2\cdot \cos(3x)\Rightarrow f'(x)=(x^2)'\cos(3x)+x^2(\cos(3x))'=2x\cos(3x)-3x^2\sin(3x)$ | |||
=== b) === | === b) === | ||
''' 1) ''' Delvis integrasjon gir at | ''' 1) ''' Delvis integrasjon gir at $\int 5x\cdot e^{2x}\,dx=5\int x\cdot e^{2x}\,dx=5[\frac{1}{2}xe^{2x}]-\frac{5}{2}\int e^{2x}\,dx=\frac{5}{4}(2x-1)e^{2x}+C$ | ||
''' 2) ''' La | ''' 2) ''' La $u=x^2-1$ så $du=2xdx$, og $\int \frac{6x}{x^2-1}\,dx=\int \frac{3}{u}\,du=3\ln|u|+C=3\ln(|x^2-1|)+C$ | ||
=== c) === | === c) === | ||
Vi multipliserer med integrerende faktor < | Vi multipliserer med integrerende faktor <math>e^{\int -2\,dx}\,\,=e^{-2x}</math> og får at <math>y'e^{-2x}-2e^{-2x}y=3e^{-2x}</math>. Omskrivning av venstresida gir at <math>(ye^{-2x})'=3e^{-2x}</math>. Integrasjon gir at <math>\int (ye^{-2x})'\,dx=ye^{-2x}=\int 3e^{-2x}\,dx=-\frac{3}{2}e^{-2x}+C</math>. Multiplikasjon med <math>e^{2x}</math> gir at <math>y=-\frac{3}{2}+Ce^{2x}</math>. Startbetingelsen gir at <math>y(0)=2=C-\frac32</math>, så <math>C=2+\frac32=\frac{7}{2}</math>, og løsningen på startverdiproblemet blir <math>y=\frac{7}{2}e^{2x}-\frac32</math> | ||
=== d) === | === d) === | ||
''' 1) ''' < | ''' 1) ''' <math>\frac12\left(\cos(u-v)+\cos(u+v)\right)=\frac12\left(\cos u \cos v +\sin u \sin v +\cos u \cos v -\sin u \sin v \right)=\cos u \cos v </math> | ||
''' 2) ''' < | ''' 2) ''' <math>(\cos x)^2=\cos x \cos x =\frac12 \left(\cos(x-x)+\cos(x+x)\right)=\frac12(1+\cos(2x))</math>. Videre er <math>\int (\cos x)^2\,dx=\int \frac12 (1+\cos(2x))\,dx=\frac12\int 1\,dx+\int \frac12 \cos(2x)\,dx=\frac12 x+\frac14\sin(2x)+C</math> | ||
=== e) === | === e) === | ||
''' 1) ''' < | ''' 1) ''' <math>\int_{-3}^2 f(x)\,dx=\int_{-3}^2 g'(x)\,dx= g(2)-g(-3)=28-6=22</math> | ||
''' 2) ''' < | ''' 2) ''' <math>f'(x)=g''(x)=h(x)</math>, så <math>\int_{-3}^1 h(x)\,dx=\int_{-3}^1 f'(x)\,dx=f(1)-f(-3)=-2-0=-2</math> | ||
| Linje 42: | Linje 41: | ||
=== a) === | === a) === | ||
< | <math> \vec{AB} = [-3, 2, 2] </math> og <math> \vec{AC} = [-2, -1, 6] </math> | ||
<p></p> | <p></p> | ||
< | <math> \vec{AB} \times \vec{AC} = [12+2,-(-18+4), 3+4]= [14, 14, 7] </math> | ||
<p></p> | <p></p> | ||
=== b) === | === b) === | ||
Normalvektoren til planet som går gjennom punktene A, B og C er < | Normalvektoren til planet som går gjennom punktene A, B og C er <math> \frac17[14, 14, 7] = [2, 2, 1]</math> | ||
<p></p> Et vilkårlig punkt i planet er < | <p></p> Et vilkårlig punkt i planet er <math>P=(x,y,z)</math>.<p></p> | ||
< | <math> \vec{AP} \cdot \vec{n} = 0 , [x-3 , y-0, z+2] \cdot [2, 2, 1] = 0 </math> | ||
< | |||
<math> \alpha: 2x + 2y + z - 4 = 0 </math> | |||
=== c) === | === c) === | ||
Siden linjen står vinkelrett på < | Siden linjen står vinkelrett på <math>\alpha</math>-planet kan vi bruke <math>[2, 2, 1]</math> som retningsvektor for linjen <math>l</math>. Linjen går gjennom <math>P = (5, 4, 4)</math>. Man får da: | ||
< | |||
<math>[x,y,z] = [5, 4, 4] + t [2, 2, 1]</math> som er ekvivalent med | |||
$ | |||
n: | n: | ||
\left [ | \left [ | ||
x = 5+ 2t\\ | x = 5+ 2t\\ | ||
y = 4 + 2t \\ | y = 4 + 2t \\ | ||
z = 4 + t \right] | z = 4 + t \right]$ | ||
I xz-planet er y = 0. Parameterfremstillingen for linjen gir da < | |||
I xz-planet er y = 0. Parameterfremstillingen for linjen gir da <math>t=-2</math>. Innsatt for x og z gir det koordinatet <math>(1, 0, 2)</math> | |||
=== d) === | === d) === | ||
Et vilkårlig punkt Q på linjen l er gitt ved parameterfremstillingen for l. Man får:<p></p> | Et vilkårlig punkt Q på linjen l er gitt ved parameterfremstillingen for l. Man får:<p></p> | ||
< | <math> V_{ABCQ} = \frac16|(\vec{AB} \times \vec {AC}) \cdot \vec{AQ}|</math> | ||
< | |||
innsatt i likningen over gir det: | <math> \vec{AQ}= [5+2t-3, 4+2t-0, 4+t+2] = [2t+2, 2t+4, t+6] </math> | ||
< | innsatt i likningen over gir det: | ||
<math> V_{ABCQ} = \frac16|[14, 14, 7] \cdot [2t+2, 2t+4, t+6] | = \frac{21}{2}|t+2|</math> | |||
=== e) === | === e) === | ||
Volumet i pyramiden skal være 42. Innsatt svaret i d gir det $\frac{21}{2}|t+2| = 42$ som gir | |||
$t + 2 = 4$ eller $t + 2 = -4$ | |||
<math>t = -6</math> eller <math>t = 2</math><p></p> | |||
Man får to løsninger, en "over", og en "under" alfa- planet. Man setter inn i parameterframstillingen for l og får: | Man får to løsninger, en "over", og en "under" alfa- planet. Man setter inn i parameterframstillingen for l og får: | ||
< | <math> Q= ( 9, 8, 6)</math> eller $Q = (-7, -8, - 2)$. | ||
= Del 2 = | = Del 2 = | ||
== | == Oppgave 3 == | ||
=== a) === | |||
Karakteristisk ligning er $\lambda^2+\frac25\lambda+\frac{26}{25}=(\lambda+\frac15-i)(\lambda+\frac15+i)=0$. Generell løsning på differensialligninga blir derfor $y(x)=Ae^{(-\frac15-i)x}+Be^{(-\frac15+i)x} | |||
$. Eulers formel gir at $e^{-ix}=\cos x -i\sin x $ og $e^{ix}=\cos x +i\sin x $, så $y(x)=Ae^{(-\frac15-i)x}+Be^{(-\frac15+i)x}=Ae^{-\frac15x}(\cos x -i\sin x )+Be^{-\frac15 x}(\cos x +i\sin x )=e^{-0.2x}(C\sin x +D\cos x )$. | |||
=== b) === | |||
== | $y(0)=5=C\sin 0 +D\cos 0 =D$ og $y(\frac{3\pi}{4})=0=e^{-0.2\cdot \frac{3\pi}{4}}(C\sin(\frac{3\pi}{4})+5\cos(\frac{3\pi}{4}))$. Eksponentialfunksjonen er positiv, så $C\sin(\frac{3\pi}{4})+5\cos(\frac{3\pi}{4})= C\frac{\sqrt{2}}{2}-5\frac{\sqrt{2}}{2}=0$. Altså er $C=5$, og $y(x)=e^{-0.2x}(C\sin x +D\cos x )=5e^{-0.2x}(\sin x +\cos x)$. | ||
== Oppgave 4 == | |||
$f(x)=5e^{-0,2x}\cdot(\sin x +\cos x )$ der $x\in\langle 0,15\rangle $ | |||
=== a) === | === a) === | ||
| Linje 102: | Linje 118: | ||
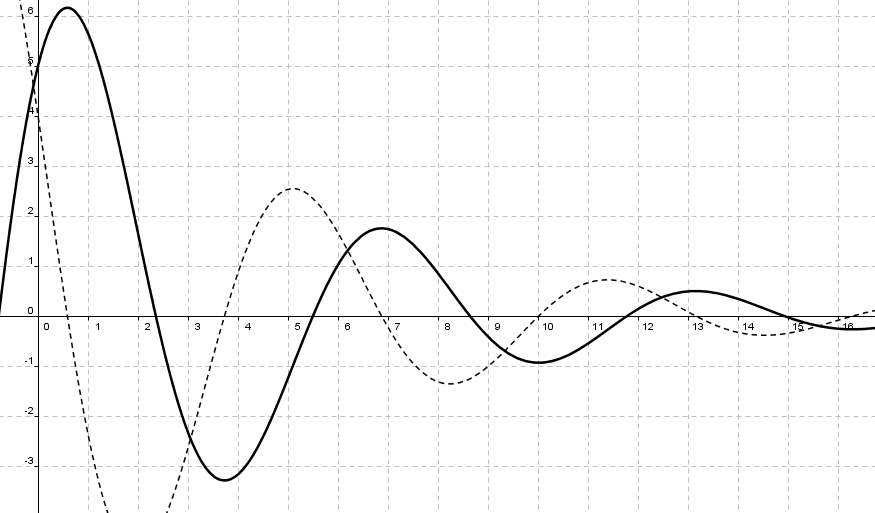
[[bilde:graf1.png]] | [[bilde:graf1.png]] | ||
<p></p> | <p></p> | ||
''Den deriverte er også med (stiplet) fordi den skal finnes i c.''<p></p> | ''Den deriverte er også med (stiplet) fordi den skal finnes i '''c)'''.''<p></p> | ||
=== b) === | === b) === | ||
Nullpunkter <p></p> | Nullpunkter <p></p> | ||
f(x)=0 <p></p> | <math>f(x)=0</math> <p></p> | ||
< | <math> 5e^{-0,2x}</math> kan aldri bli null. Man får <p></p> | ||
< | <math>\sin x + \cos x =0 \\ | ||
tan x = -1\\ | \tan x = -1\\ | ||
x= \frac{3\pi}{4} + n \cdot \pi\\ x \in \Big(( \frac{3\pi}{4},0), (\frac{7\pi}{4},0),(\frac{11\pi}{4},0),(\frac{15\pi}{4},0),(\frac{19\pi}{4},0)\Big)</ | x= \frac{3\pi}{4} + n \cdot \pi\\ x \in \Big(( \frac{3\pi}{4},0), (\frac{7\pi}{4},0),(\frac{11\pi}{4},0),(\frac{15\pi}{4},0),(\frac{19\pi}{4},0)\Big)</math> | ||
<p></p> | <p></p> | ||
Regner man om fra eksakte verdier til desimaltall, ser man at det stemmer med grafen i '''a)'''. | |||
=== c) === | === c) === | ||
< | <math> \begin{align} f^{\prime}(x) &= 5(-0,2)e^{-0,2x} \cdot (\sin x + \cos x)+5e^{-0,2x} \cdot (\cos x -\sin x) | ||
= -e^{-0,2x} \cdot sin x -e^{-0,2x} \cdot cos x +5e^{-0,2x} \cdot cos x - 5e^{-0,2x} \cdot sin x \\ | \\ &= -e^{-0,2x} \cdot \sin x -e^{-0,2x} \cdot \cos x +5e^{-0,2x} \cdot \cos x - 5e^{-0,2x} \cdot \sin x \\ &= | ||
4e^{-0,2x} \cdot cos x - 6e^{-0,2x} \cdot sin x =2e^{-0,2x} \cdot ( | 4e^{-0,2x} \cdot \cos x - 6e^{-0,2x} \cdot \sin x \\ &=2e^{-0,2x} \cdot (2\cos x-3\sin x) \end{align} </math> | ||
=== d) === | === d) === | ||
Man har et toppunkt hver gang den deriverte skifter fortegn fra positiv til negativ. Ved å løse < | Man har et toppunkt hver gang den deriverte skifter fortegn fra positiv til negativ. Ved å løse <math>2\cos(x)-3\sin(x) = 0</math> og å tegne fortegnslinje, finner man at det er tilfelle for <math>x=0.59</math> , <math>x=6.87</math> og for <math>x= 13.15</math>. Sett disse x-verdiene inn i funksjonsuttrykket og man får funksjonsverdien til toppunktene. | ||
e) | === e) === | ||
<p></p> | <math> A= \sqrt{a^2 + b^2} = \sqrt2</math> Punktet <math>(1,1)</math> ligger i første kvadrant. <math> \tan\phi = 1</math>. Man får da:<p></p> | ||
<math> f(x)=5e^{-0,2x} \cdot \sqrt2\cdot \sin(x + \frac{\pi}{4}) = 5\sqrt2e^{-0,2x} \cdot \sin(x + \frac{\pi}{4}) </math> | |||
=== f) === | === f) === | ||
< | <math>\sin(x + \frac{\pi}{4})</math> varierer i verdi mellom <math>-1</math> og <math>1</math>, avhengig av <math>x</math>. Derfor ligger $f(x)$ mellom $q$ og $p$, altså i området | ||
< | <math> \pm 5\sqrt{2}e^{-0,2x}</math> | ||
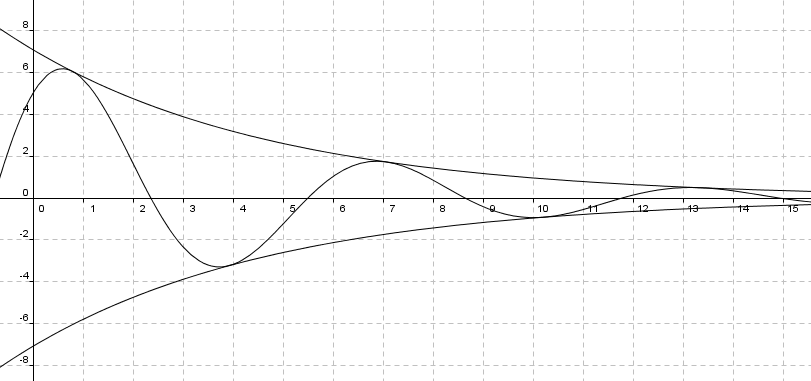
[[bilde:4f.png]] | [[bilde:4f.png]] | ||
== | == Oppgave 5 == | ||
=== a) === | |||
Eksponentialfunksjonen er alltid positiv, så for å finne nullpunktene må vi løse ligningen $\sin x +\cos x =0$. Denne kan omskrives til $\frac{\sin x }{\cos x }=\tan x =-1$, så $x=\tan^{-1}(-1)=-\frac{\pi}{4}+n\pi=\frac{3\pi}{4}+(n-1)\pi\approx 2.356+(n-1)\pi$ | |||
=== b) === | |||
Nullpunktene danner en aritmetisk progresjon på formen $a_n=a_1+(n-1)d$. Dersom $n=10$ er $x_{10}=2.356+9\pi\approx 30.63$, så vi må ha at $1\leq n\leq 9$. Altså er det $9$ nullpunkt i intervallet $x\in\langle 0,30\rangle$ | |||
=== c) === | |||
Toppunktene kan skrives $5e^{-0.2x}, 5e^{-0.2(x+2\pi)}, 5e^{-0.2(x+4\pi)}$, altså på formen $ak^n=5e^{-0.2x}(e^{-0.4\pi})^n$, der $a=5e^{-0.4x}=6.164$ og $n=0,1,2$. Det neste leddet i følgen blir dermed $6.164 (e^{-0.4\pi})^3\approx 0.142$. | |||
=== d) === | |||
Vi får rekka $\sum_{n=0}^{\infty} 6.164(e^{-0.4\pi})^n$. Siden $|e^{-0.4\pi}|\approx 0.285<1$ vil rekka konvergere. | |||
Summeformelen for geometriske rekker gir at $\sum_{n=0}^{\infty} 6.164(e^{-0.4\pi})^n\approx 6.164\lim_{n\to\infty}\frac{1-0.285^n}{1-0.285}\approx 8.62$ | |||
== Oppgave 6 == | |||
=== Alternativ I === | |||
==== a) ==== | |||
Siden <math>v=y'</math> og <math>a=y''</math> kan vi skrive ligningen <math>-b\cdot v-k\cdot y=m\cdot a</math> som <math>-b\cdot y'-k\cdot y=m\cdot y''</math>. Vi deler med <math>m</math> og får at <math>y''+\frac{b}{m}y'+\frac{k}{m}y=0</math> | |||
==== b) ==== | |||
Med $b=1$, $k=2.6$ og $m=2.5$ blir ligningen | |||
$y^{\prime \prime}+\frac{1}{2.5}y'+\frac{2.6}{2.5}y=y^{\prime\prime}+\frac{2}{5}y'+\frac{26}{25}y=0$ | |||
Fra '''3b)''' vet vi at løsningen på startverdiproblemet er $y(t)=5e^{-0.2t}(\sin t +\cos t )$ | |||
==== c) ==== | |||
<math>\sin(t)+\cos(t)</math> er periodisk med periode <math>2\pi</math>, og avstanden mellom nullpunktene er <math>\pi</math>. | |||
==== d) ==== | |||
Forholdet mellom to påfølgende maksimale utslag er <math>\frac{5e^{-0.2(t+2\pi)}}{5e^{-0.2t}}=e^{-0.4\pi}\approx 0.285</math>, så det maksimale utslaget minker med <math>1-0.285=0.715=71.5\%</math> | |||
=== Alternativ II === | |||
==== a) ==== | |||
La <math>S_n=\sum_{k=1}^n k</math>. Vi grupperer tallene i par <math>\{1,n\}, \{2,n-1\},...</math>. Det er <math>\frac{n}{2}</math> slike par og summen i hvert par er <math>n+1</math>, altså blir <math>S_n=\frac{n}{2}\cdot (n+1)=\frac{n(n+1)}{2}</math> | |||
<math>S_8=\frac{8\cdot 9}{2}=36</math> | |||
==== b) ==== | |||
Ved bruk av digitalt verktøy beregner vi at <math>s_{15}=14400</math> og <math>s_{16}=18496</math>, så vi behøver <math>16</math> ledd for å overstige <math>15000</math>. | |||
==== c) ==== | |||
'''Induksjonssteg 1:''' <math>1=\frac{1^2\cdot 2^2}{4}</math>, så formelen er riktig for <math>n=1</math>. | |||
'''Induksjonssteg 2:''' Anta at formelen er riktig for <math>n=k</math>. Da er <math>s_k=\frac{k^2(k+1)^2}{4}</math>, og <math>s_{k+1}=s_k+(k+1)^3=\frac{k^2(k+1)^2}{4}+(k+1)^3=(\frac{k^2}{4}+k+1)(k+1)^2=\frac{k^2+4k+4}{4}(k+1)^2=\frac{(k+1)^2(k+2)^2}{4}</math>, så formelen er riktig for <math>n=k+1</math>. Det følger at formelen er riktig for alle naturlige tall. | |||
==== d) ==== | |||
== | <math>(1+2+3+...+n)^2=(\frac{n(n+1)}{2})^2=\frac{n^2(n+1)^2}{4}=1^3+2^3+3^3+...+n^3</math> | ||
Siste sideversjon per 16. mai 2013 kl. 18:49
Del 1
Oppgave 1
a)
$f(x)=x^2\cdot \cos(3x)\Rightarrow f'(x)=(x^2)'\cos(3x)+x^2(\cos(3x))'=2x\cos(3x)-3x^2\sin(3x)$
b)
1) Delvis integrasjon gir at $\int 5x\cdot e^{2x}\,dx=5\int x\cdot e^{2x}\,dx=5[\frac{1}{2}xe^{2x}]-\frac{5}{2}\int e^{2x}\,dx=\frac{5}{4}(2x-1)e^{2x}+C$
2) La $u=x^2-1$ så $du=2xdx$, og $\int \frac{6x}{x^2-1}\,dx=\int \frac{3}{u}\,du=3\ln|u|+C=3\ln(|x^2-1|)+C$
c)
Vi multipliserer med integrerende faktor <math>e^{\int -2\,dx}\,\,=e^{-2x}</math> og får at <math>y'e^{-2x}-2e^{-2x}y=3e^{-2x}</math>. Omskrivning av venstresida gir at <math>(ye^{-2x})'=3e^{-2x}</math>. Integrasjon gir at <math>\int (ye^{-2x})'\,dx=ye^{-2x}=\int 3e^{-2x}\,dx=-\frac{3}{2}e^{-2x}+C</math>. Multiplikasjon med <math>e^{2x}</math> gir at <math>y=-\frac{3}{2}+Ce^{2x}</math>. Startbetingelsen gir at <math>y(0)=2=C-\frac32</math>, så <math>C=2+\frac32=\frac{7}{2}</math>, og løsningen på startverdiproblemet blir <math>y=\frac{7}{2}e^{2x}-\frac32</math>
d)
1) <math>\frac12\left(\cos(u-v)+\cos(u+v)\right)=\frac12\left(\cos u \cos v +\sin u \sin v +\cos u \cos v -\sin u \sin v \right)=\cos u \cos v </math>
2) <math>(\cos x)^2=\cos x \cos x =\frac12 \left(\cos(x-x)+\cos(x+x)\right)=\frac12(1+\cos(2x))</math>. Videre er <math>\int (\cos x)^2\,dx=\int \frac12 (1+\cos(2x))\,dx=\frac12\int 1\,dx+\int \frac12 \cos(2x)\,dx=\frac12 x+\frac14\sin(2x)+C</math>
e)
1) <math>\int_{-3}^2 f(x)\,dx=\int_{-3}^2 g'(x)\,dx= g(2)-g(-3)=28-6=22</math>
2) <math>f'(x)=g(x)=h(x)</math>, så <math>\int_{-3}^1 h(x)\,dx=\int_{-3}^1 f'(x)\,dx=f(1)-f(-3)=-2-0=-2</math>
Oppgave 2
a)
<math> \vec{AB} = [-3, 2, 2] </math> og <math> \vec{AC} = [-2, -1, 6] </math>
<math> \vec{AB} \times \vec{AC} = [12+2,-(-18+4), 3+4]= [14, 14, 7] </math>
b)
Normalvektoren til planet som går gjennom punktene A, B og C er <math> \frac17[14, 14, 7] = [2, 2, 1]</math>
Et vilkårlig punkt i planet er <math>P=(x,y,z)</math>.
<math> \vec{AP} \cdot \vec{n} = 0 , [x-3 , y-0, z+2] \cdot [2, 2, 1] = 0 </math>
<math> \alpha: 2x + 2y + z - 4 = 0 </math>
c)
Siden linjen står vinkelrett på <math>\alpha</math>-planet kan vi bruke <math>[2, 2, 1]</math> som retningsvektor for linjen <math>l</math>. Linjen går gjennom <math>P = (5, 4, 4)</math>. Man får da:
<math>[x,y,z] = [5, 4, 4] + t [2, 2, 1]</math> som er ekvivalent med
$ n: \left [ x = 5+ 2t\\ y = 4 + 2t \\ z = 4 + t \right]$
I xz-planet er y = 0. Parameterfremstillingen for linjen gir da <math>t=-2</math>. Innsatt for x og z gir det koordinatet <math>(1, 0, 2)</math>
d)
Et vilkårlig punkt Q på linjen l er gitt ved parameterfremstillingen for l. Man får:
<math> V_{ABCQ} = \frac16|(\vec{AB} \times \vec {AC}) \cdot \vec{AQ}|</math>
<math> \vec{AQ}= [5+2t-3, 4+2t-0, 4+t+2] = [2t+2, 2t+4, t+6] </math>
innsatt i likningen over gir det:
<math> V_{ABCQ} = \frac16|[14, 14, 7] \cdot [2t+2, 2t+4, t+6] | = \frac{21}{2}|t+2|</math>
e)
Volumet i pyramiden skal være 42. Innsatt svaret i d gir det $\frac{21}{2}|t+2| = 42$ som gir
$t + 2 = 4$ eller $t + 2 = -4$
<math>t = -6</math> eller <math>t = 2</math>
Man får to løsninger, en "over", og en "under" alfa- planet. Man setter inn i parameterframstillingen for l og får:
<math> Q= ( 9, 8, 6)</math> eller $Q = (-7, -8, - 2)$.
Del 2
Oppgave 3
a)
Karakteristisk ligning er $\lambda^2+\frac25\lambda+\frac{26}{25}=(\lambda+\frac15-i)(\lambda+\frac15+i)=0$. Generell løsning på differensialligninga blir derfor $y(x)=Ae^{(-\frac15-i)x}+Be^{(-\frac15+i)x} $. Eulers formel gir at $e^{-ix}=\cos x -i\sin x $ og $e^{ix}=\cos x +i\sin x $, så $y(x)=Ae^{(-\frac15-i)x}+Be^{(-\frac15+i)x}=Ae^{-\frac15x}(\cos x -i\sin x )+Be^{-\frac15 x}(\cos x +i\sin x )=e^{-0.2x}(C\sin x +D\cos x )$.
b)
$y(0)=5=C\sin 0 +D\cos 0 =D$ og $y(\frac{3\pi}{4})=0=e^{-0.2\cdot \frac{3\pi}{4}}(C\sin(\frac{3\pi}{4})+5\cos(\frac{3\pi}{4}))$. Eksponentialfunksjonen er positiv, så $C\sin(\frac{3\pi}{4})+5\cos(\frac{3\pi}{4})= C\frac{\sqrt{2}}{2}-5\frac{\sqrt{2}}{2}=0$. Altså er $C=5$, og $y(x)=e^{-0.2x}(C\sin x +D\cos x )=5e^{-0.2x}(\sin x +\cos x)$.
Oppgave 4
$f(x)=5e^{-0,2x}\cdot(\sin x +\cos x )$ der $x\in\langle 0,15\rangle $
a)
Grafen ser slik ut:
Den deriverte er også med (stiplet) fordi den skal finnes i c).
b)
Nullpunkter
<math>f(x)=0</math>
<math> 5e^{-0,2x}</math> kan aldri bli null. Man får
<math>\sin x + \cos x =0 \\ \tan x = -1\\ x= \frac{3\pi}{4} + n \cdot \pi\\ x \in \Big(( \frac{3\pi}{4},0), (\frac{7\pi}{4},0),(\frac{11\pi}{4},0),(\frac{15\pi}{4},0),(\frac{19\pi}{4},0)\Big)</math>
Regner man om fra eksakte verdier til desimaltall, ser man at det stemmer med grafen i a).
c)
<math> \begin{align} f^{\prime}(x) &= 5(-0,2)e^{-0,2x} \cdot (\sin x + \cos x)+5e^{-0,2x} \cdot (\cos x -\sin x) \\ &= -e^{-0,2x} \cdot \sin x -e^{-0,2x} \cdot \cos x +5e^{-0,2x} \cdot \cos x - 5e^{-0,2x} \cdot \sin x \\ &= 4e^{-0,2x} \cdot \cos x - 6e^{-0,2x} \cdot \sin x \\ &=2e^{-0,2x} \cdot (2\cos x-3\sin x) \end{align} </math>
d)
Man har et toppunkt hver gang den deriverte skifter fortegn fra positiv til negativ. Ved å løse <math>2\cos(x)-3\sin(x) = 0</math> og å tegne fortegnslinje, finner man at det er tilfelle for <math>x=0.59</math> , <math>x=6.87</math> og for <math>x= 13.15</math>. Sett disse x-verdiene inn i funksjonsuttrykket og man får funksjonsverdien til toppunktene.
e)
<math> A= \sqrt{a^2 + b^2} = \sqrt2</math> Punktet <math>(1,1)</math> ligger i første kvadrant. <math> \tan\phi = 1</math>. Man får da:
<math> f(x)=5e^{-0,2x} \cdot \sqrt2\cdot \sin(x + \frac{\pi}{4}) = 5\sqrt2e^{-0,2x} \cdot \sin(x + \frac{\pi}{4}) </math>
f)
<math>\sin(x + \frac{\pi}{4})</math> varierer i verdi mellom <math>-1</math> og <math>1</math>, avhengig av <math>x</math>. Derfor ligger $f(x)$ mellom $q$ og $p$, altså i området <math> \pm 5\sqrt{2}e^{-0,2x}</math>
Oppgave 5
a)
Eksponentialfunksjonen er alltid positiv, så for å finne nullpunktene må vi løse ligningen $\sin x +\cos x =0$. Denne kan omskrives til $\frac{\sin x }{\cos x }=\tan x =-1$, så $x=\tan^{-1}(-1)=-\frac{\pi}{4}+n\pi=\frac{3\pi}{4}+(n-1)\pi\approx 2.356+(n-1)\pi$
b)
Nullpunktene danner en aritmetisk progresjon på formen $a_n=a_1+(n-1)d$. Dersom $n=10$ er $x_{10}=2.356+9\pi\approx 30.63$, så vi må ha at $1\leq n\leq 9$. Altså er det $9$ nullpunkt i intervallet $x\in\langle 0,30\rangle$
c)
Toppunktene kan skrives $5e^{-0.2x}, 5e^{-0.2(x+2\pi)}, 5e^{-0.2(x+4\pi)}$, altså på formen $ak^n=5e^{-0.2x}(e^{-0.4\pi})^n$, der $a=5e^{-0.4x}=6.164$ og $n=0,1,2$. Det neste leddet i følgen blir dermed $6.164 (e^{-0.4\pi})^3\approx 0.142$.
d)
Vi får rekka $\sum_{n=0}^{\infty} 6.164(e^{-0.4\pi})^n$. Siden $|e^{-0.4\pi}|\approx 0.285<1$ vil rekka konvergere.
Summeformelen for geometriske rekker gir at $\sum_{n=0}^{\infty} 6.164(e^{-0.4\pi})^n\approx 6.164\lim_{n\to\infty}\frac{1-0.285^n}{1-0.285}\approx 8.62$
Oppgave 6
Alternativ I
a)
Siden <math>v=y'</math> og <math>a=y</math> kan vi skrive ligningen <math>-b\cdot v-k\cdot y=m\cdot a</math> som <math>-b\cdot y'-k\cdot y=m\cdot y</math>. Vi deler med <math>m</math> og får at <math>y+\frac{b}{m}y'+\frac{k}{m}y=0</math>
b)
Med $b=1$, $k=2.6$ og $m=2.5$ blir ligningen
$y^{\prime \prime}+\frac{1}{2.5}y'+\frac{2.6}{2.5}y=y^{\prime\prime}+\frac{2}{5}y'+\frac{26}{25}y=0$
Fra 3b) vet vi at løsningen på startverdiproblemet er $y(t)=5e^{-0.2t}(\sin t +\cos t )$
c)
<math>\sin(t)+\cos(t)</math> er periodisk med periode <math>2\pi</math>, og avstanden mellom nullpunktene er <math>\pi</math>.
d)
Forholdet mellom to påfølgende maksimale utslag er <math>\frac{5e^{-0.2(t+2\pi)}}{5e^{-0.2t}}=e^{-0.4\pi}\approx 0.285</math>, så det maksimale utslaget minker med <math>1-0.285=0.715=71.5\%</math>
Alternativ II
a)
La <math>S_n=\sum_{k=1}^n k</math>. Vi grupperer tallene i par <math>\{1,n\}, \{2,n-1\},...</math>. Det er <math>\frac{n}{2}</math> slike par og summen i hvert par er <math>n+1</math>, altså blir <math>S_n=\frac{n}{2}\cdot (n+1)=\frac{n(n+1)}{2}</math>
<math>S_8=\frac{8\cdot 9}{2}=36</math>
b)
Ved bruk av digitalt verktøy beregner vi at <math>s_{15}=14400</math> og <math>s_{16}=18496</math>, så vi behøver <math>16</math> ledd for å overstige <math>15000</math>.
c)
Induksjonssteg 1: <math>1=\frac{1^2\cdot 2^2}{4}</math>, så formelen er riktig for <math>n=1</math>.
Induksjonssteg 2: Anta at formelen er riktig for <math>n=k</math>. Da er <math>s_k=\frac{k^2(k+1)^2}{4}</math>, og <math>s_{k+1}=s_k+(k+1)^3=\frac{k^2(k+1)^2}{4}+(k+1)^3=(\frac{k^2}{4}+k+1)(k+1)^2=\frac{k^2+4k+4}{4}(k+1)^2=\frac{(k+1)^2(k+2)^2}{4}</math>, så formelen er riktig for <math>n=k+1</math>. Det følger at formelen er riktig for alle naturlige tall.
d)
<math>(1+2+3+...+n)^2=(\frac{n(n+1)}{2})^2=\frac{n^2(n+1)^2}{4}=1^3+2^3+3^3+...+n^3</math>