R2 2011 vår LØSNING

Del 1

Oppgave 1

a)

1) $f(x)=2\sin (2x)\Rightarrow f^{\prime }(x)=4\cos (2x)$

2) $g(x)=x^2\cos (2x)\Rightarrow g^{\prime }(x)=(x^2{)}^{\prime }\cos (2x)+x^2(\cos (2x){)}^{\prime }=2x\cos (2x)-2x^2\sin (2x)$

3) $h(x)=\frac{1}{2}\sqrt{x^2-4x}\Rightarrow h^{\prime }(x)=\frac{1}{2}\frac{x-2}{\sqrt{x^2-4x}}$

b)

1) Delvis integrasjon gir at $\int x{e}^{x}dx=[x{e}^x]-\int e^{x}dx=(x-1)e^x+C$

2) $\int \frac{5x+3}{x^2-9}dx=\int \frac{5x+3}{(x-3)(x+3)}dx$. Delbrøksoppspaltning gir at

$\frac{1}{(x-3)(x+3)}=\frac{1}{6}(\frac{1}{x-3}-\frac{1}{x+3})$, så $\int \frac{5x+3}{(x-3)(x+3)}dx=\int (5x+3)\frac{1}{6}(\frac{1}{x-3}-\frac{1}{x+3})dx=\frac{1}{6}(\int \frac{5x+3}{x-3}dx-\int \frac{5x+3}{x+3}dx)$

$\int \frac{5x+3}{x-3}dx=\int \frac{5(x-3)+18}{x-3}dx=5\int dx+18\int \frac{1}{x-3}dx=5x+18\ln (|x-3|)+C_1$ og

$\int \frac{5x+3}{x+3}dx=\int \frac{5(x+3)-12}{x+3}dx=5\int dx-12\int \frac{1}{x+3}dx=5x-12\ln (|x+3|)+C_2$, så

$\frac{1}{6}(\int \frac{5x+3}{x-3}dx-\int \frac{5x+3}{x+3}dx)=3\ln (|x-3|)+2\ln (|x+3|)+C$

c)

Sirkelen på figuren er beskrevet ved ligningen $x^2+y^2=1$, så høyden opp til halvsirkelen i øvre halvplan som funksjon av $x$, er $y(x)=\sqrt{1-x^2}$. Arealet av halvsirkelen i øvre halvplan er derfor ${\int }_{-1}^{1}y(x)dx={\int }_{-1}^1\sqrt{1-x^2}dx=\frac{1}{2}\pi (1{)}^2=\frac{1}{2}\pi$

d)

1) Dersom én av vektorene har lengde $0$ vil prikkproduktet være $0$. Anta videre at begge vektorene har lengde ulik $0$. Siden prikkproduktet er $0$, må vektorene $\overrightarrow{a}$ og $\overrightarrow{b}$ stå normalt på hverandre.

2) Dersom én av vektorene har lengde $0$ vil kryssproduktet være $0$. Anta videre at begge vektorene har lengde ulik $0$. Siden kryssproduktet er $0$, må vektorene $\overrightarrow{a}$ og $\overrightarrow{b}$ ligge parallelt.

e)

Beregner først vektorene $\overrightarrow{AB}=(2-1,-1-1,3-(-1))=(1,-2,4)$ og $\overrightarrow{AC}=(3-1,2-1,2-(-1))=(2,1,3)$. Kryssproduktet $\overrightarrow{AB}\times \overrightarrow{AC}=(-2\cdot 3-(1\cdot 4),-(1\cdot 3-2\cdot 4),1\cdot 1-2\cdot (-2))=(-10,5,5)$. For å vise at $\overrightarrow{AB}\times \overrightarrow{AC}$ står vinkelrett på både $\overrightarrow{AB}$ og $\overrightarrow{AC}$, beregner vi $(\overrightarrow{AB}\times \overrightarrow{AC})\cdot \overrightarrow{AB}$ og $(\overrightarrow{AB}\times \overrightarrow{AC})\cdot \overrightarrow{AC}$ og viser at disse er $0$:

$(\overrightarrow{AB}\times \overrightarrow{AC})\cdot \overrightarrow{AB}=(-10,5,5)\cdot (1,-2,4)=-10-10+20=0$ og

$(\overrightarrow{AB}\times \overrightarrow{AC})\cdot \overrightarrow{AC}=(-10,5,5)\cdot (2,1,3)=-20+5+15=0$.

f)

Induksjonssteg 1: $1=\frac{4^1-1}{3}$, så formelen er riktig for $n=1$

Induksjonssteg 2: Anta at formelen er riktig for $n=k$, så $1+4+16+...+4^{k-1}=\frac{4^k-1}{3}$. Da er $1+4+16+...+4^{k-1}+4^k=\frac{4^k-1}{3}+4^k=\frac{4^k-1+3\cdot 4^k}{3}=\frac{(1+3)4^k-1}{3}=\frac{4^{k+1}-1}{3}$, så formelen er riktig for $n=k+1$, og vi er ferdige.

Oppgave 2

a)

Vi multipliserer den førsteordens differensialligningen $y^{\prime }-2y=5$ med integrerende faktor $e^{\int -2dx}=e^{-2x}$, og får

$e^{-2x}{y}^{\prime }-2e^{-2x}y=5e^{-2x}$. Venstresiden kan nå omskrives:

$(e^{-2x}y{)}^{\prime }=5e^{-2x}$

Vi integrerer ligningen med hensyn på $x$:

$$\begin{gathered} \int (e^{-2x}y{)}^{\prime }dx=\int 5e^{-2x}dx \\ {e}^{-2x}y=-\frac{5}{2}{e}^{-2x}+C \end{gathered}$$, og løser for $y$:

$y=-\frac{5}{2}+C{e}^{2x}$. Løsningen verfiseres ved innsetting i den opprinnelige diff.ligningen:

$y^{\prime }=2C{e}^{2x}$, så $y^{\prime }-2y=2C{e}^{2x}-2(-\frac{5}{2}+C{e}^{2x})=5$.

b)

1) $y(0)=-\frac{5}{2}+C=2$, så $C=2+\frac{5}{2}=\frac{9}{2}$

2) Setter inn $y=\frac{49}{2}$ i løsningen, og løser for $x$:

$$\begin{gathered} \frac{49}{2}=-\frac{5}{2}+\frac{9}{2}{e}^{2x} \\ \frac{54}{9}=6=e^{2x} \\ \ln (6)=2x \\ x=\frac{\ln (6)}{2}\approx \frac{1.8}{2}=0.9 \end{gathered}$$

c)

Tangenten i $(0,2)$ har ligning $y=ax+b$, der $a=(-\frac{5}{2}+\frac{9}{2}{e}^{2x}{)}^{\prime }(0)=\frac{18}{2}=9$. I tillegg må punktet $(0,2)$ ligge på tangentlinja, så $2=a\cdot 0+b$. Ligningen til tangenten er derfor $y=9x+2$.

Del 2

Oppgave 3

a)

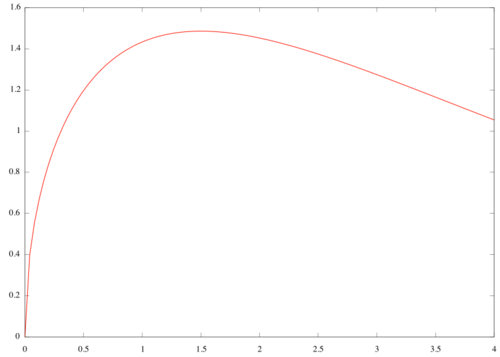
Finner toppunktet ved derivasjon av funksjonen $f(x)=2\sqrt{x}{e}^{-\frac{x}{3}}$: $f^{\prime }(x)=\frac{(3-2x)e^{-\frac{x}{3}}}{3\sqrt{x}}$. Den deriverte er $0$ når $3-2x=0$, så toppunktet er i $x=\frac{3}{2}$. Diameteren til skaftet er størst i toppunktet til grafen til $f(x)$. Størst mulig diameter er derfor $2\cdot f(\frac{3}{2})=4\sqrt{\frac{3}{2}}{e}^{-\frac{1}{2}}\approx 2.97$.

b)

Volumet er gitt ved ${\int }_0^4\pi f(x{)}^{2}dx=4\pi {\int }_0^{4}x{e}^{-\frac{2}{3}x}dx$. La $u=-\frac{2}{3}x$. Integralet blir $9\pi \int u{e}^{u}du$. Vi bruker resultatet fra oppgave 1b),1): $9\pi \int u{e}^{u}du=9\pi [(u-1)e^u]=9\pi [(-\frac{2}{3}x-1)e^{-\frac{2}{3}x}{]}_0^4=9\pi ((-\frac{8}{3}-1)e^{-\frac{8}{3}}+1)=9\pi (-\frac{11}{3}{e}^{-\frac{8}{3}}+1)$

Oppgave 4

a)

1) La $A_0=A$ og $B_0=B$. Generelt kan vi skrive arealet av trapeset $A_n{B}_n{B}_{n+1}{A}_{n+1}$ som $(A_n{B}_n+A_{n+1}{B}_{n+1})\frac{B_n{B}_{n+1}}{2}$, der $A_0{B}_0=8$, $B_0{B}_1=8$, $B_n{B}_{n+1}=\frac{16}{2^{n+1}}$, $\frac{A_n{B}_n}{B_n{B}_{n+1}}=\frac{8}{8}=1$ (ved formlikhet av trapesene). Altså er $A_n{B}_n=B_n{B}_{n+1}=\frac{16}{2^{n+1}}$ og arealet av trapeset $A_n{B}_n{B}_{n+1}{A}_{n+1}$ blir $(A_n{B}_n+A_{n+1}{B}_{n+1})\frac{B_n{B}_{n+1}}{2}=(\frac{16}{2^{n+1}}+\frac{16}{2^{n+2}})\frac{16}{2^{n+2}}=\frac{3\cdot {16}^2}{2^{2n+4}}=3\cdot 2^{4-2n}$. Summen av arealene til trapesene blir derfor

$\sum _{n=0}^{\mathrm{\infty }}3\cdot 2^{4-2n}=48+12+3+...$

2) Fra forrige deloppgave ser vi at summen av arealene er en geometrisk rekke

$\sum _{n=0}^{\mathrm{\infty }}3\cdot 2^{4-2n}=48\sum _{n=0}^{\mathrm{\infty }}(\frac{1}{4}{)}^n$

Rekken konvergerer siden $|\frac{1}{4}|<1$

b)

Geometrisk ser vi at summen av arealene må konvergere mot arealet av $\mathrm{△}ABC$, som er $\frac{8\cdot 16}{2}=64$

Summeformelen for en geometrisk rekke $\sum _{k=0}^{n-1}a{r}^k=a\frac{1-r^n}{1-r}$ gir at

$\underset{n\to \mathrm{\infty }}{lim}\sum _{k=0}^{n-1}48(\frac{1}{4}{)}^k=48\underset{n\to \mathrm{\infty }}{lim}\frac{1-{\frac{1}{4}}^n}{\frac{3}{4}}=48\cdot \frac{4}{3}=64$.

Oppgave 5

a)

I $xy$-planet er $z=0$, så vi må ha at $0=4+2t$. Altså er $t=-2$ i punkt $A$. I $xz$-planet er $y=0$, så vi må ha at $0=3+t$. Altså er $t=-3$ i punkt $B$. Koordinatene til $A$ og $B$ er derfor gitt ved $A(5+2\cdot 2,3-2,0)=A(9,1,0)$ og $B(5-2\cdot (-3),0,4+2\cdot (-3))=B(11,0,-2)$. Avstanden mellom $A$ og $B$ er derfor $|(11-9,0-1,-2-0)|=|(2,-1,-2)|=\sqrt{2^2+1^2+2^2}=\sqrt{9}=3$

b)

Vi kan skrive linja $l$ på formen $(x,y,z)=(5-2t,3+t,4+2t)=(5,3,4)+t(-2,1,2)$. Det betyr at vektoren $(-2,1,2)$ angir retningen til linja $l$. På samme måte kan linja $m$ skrives som $(x,y,z)=(s,1-s,1+s)=(0,1,1)+s(1,-1,1)$, der vektoren $(1,-1,1)$ angir retningen. Linjene er parallelle hvis og bare hvis det fins en konstant $k$ slik at $(-2,1,2)=k(1,-1,1)$. Utfra ligningen ser vi at det ikke fins en slik $k$, altså er linjene ikke parallelle.

c)

Et tilfeldig punkt P på l er angitt ved koordinatet $(x,y,z)=(5-2t,3+t,4+2t)$, og et punkt $Q$ på $m$ er gitt ved $(x,y,z)=(s,1-s,1+s)$. $\overrightarrow{PQ}=(s,1-s,1+s)-(5-2t,3+t,4+2t)=(s+2t-5,-s-t-2,s-2t-3)$

d)

For at $\overrightarrow{PQ}$ skal stå vinkelrett på linjene $m$ og $l$, må $(s+2t-5,-s-t-2,s-2t-3)\cdot (-2,1,2)=0=(s+2t-5,-s-t-2,s-2t-3)\cdot (1,-1,1)$. Vi får dermed ligningene $-2s-4t+10-s-t-2+2s-4t-6=-s-9t+2=0$ og $s+2t-5+s+t+2+s-2t-3=3s+t-6=0$. Altså er $3s+t-6-3s-27t+6=-26t=0$, så vi må ha at $t=0$. Da er $s=2$. Vi får da punktene $P(5,3,4)$ og $Q(2,-1,3)$

e)

$|\overrightarrow{PQ}|=|(2,-1,3)-(5,3,4)|=|(-3,-4,-1)|=\sqrt{3^2+4^2+1^2}=\sqrt{9+16+1}=\sqrt{26}$

Oppgave 6

a)

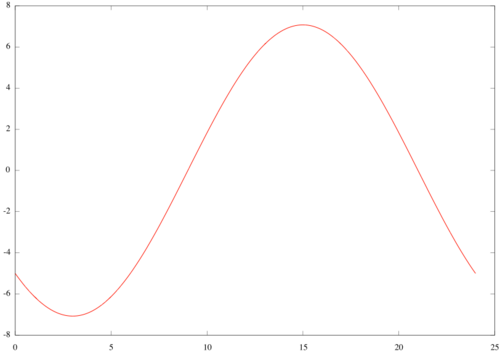
Avleser fra figuren at amplituden er $\approx 7$, og perioden $24$.

b)

Den deriverte av $f(x)$ er $f^{\prime }(x)=-\frac{5}{12}\pi (\cos (\frac{\pi }{12}x)-\sin (\frac{\pi }{12}x))$, og har nullpunkt i $x=3$ og $x=15$. Den deriverte er positiv når $3<x<15$, så funksjonen $f(x)$ har toppunkt i $x=15$ og bunnpunkt i $x=3$.

c)

Vi ser at $g(x)=22+f(x)$. Funksjonene $f(x)$ og $g(x)$ må derfor ha topp- og bunnpunkter i samme (korresponderende) $x$-verdier. Laveste temperatur inntreffer for $x=3$. Da er temperaturen $g(3)=22-5\sin (\frac{3\pi }{12})-5\cos (\frac{3\pi }{12})=22-5\sqrt{2}\approx 14.93$ grader Celsius. Høyeste temperatur inntreffer for $x=15$. Da er temperaturen $g(15)=22-5\sin (\frac{15\pi }{12})-5\cos (\frac{15\pi }{12})=22+5\sqrt{2}\approx 29.07$ grader Celsius.

Oppgave 7

a)

b)

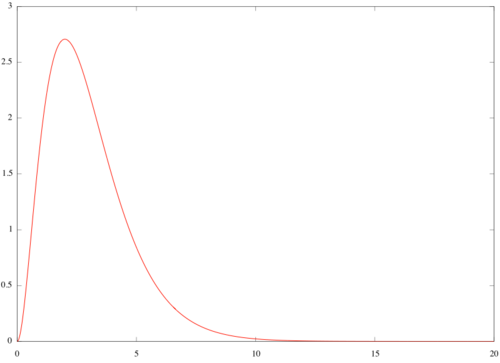
1) La $f(x)=5x^2{e}^{-x}$. Produktregelen gir at $f^{\prime }(x)=(5x^2{)}^{\prime }{e}^{-x}+5x^2(e^{-x}{)}^{\prime }=10x{e}^{-x}-5x^2{e}^{-x}=5(2x-x^2)e^{-x}$. (Vi har i tillegg brukt kjerneregelen, og derivasjonsreglene $(e^x{)}^{\prime }=e^x$ og $(x^n{)}^{\prime }=n{x}^{n-1}$).

2) Eksponentialfunksjonen er alltid positiv, så det er tilstrekkelig å betrakte nullpunktene til $2x-x^2=x(2-x)$ i uttrykket for den deriverte, som er $x=0$ og $x=2$. Når $0<x<2$ er $f^{\prime }(x)>0$ og når $x>2$ er $f^{\prime }(x)<0$, så funksjonen $f(x)$ vokser i intervallet $(0,2)$ og avtar i $(2,\mathrm{\infty })$. $f(x)$ har derfor et toppunkt i $x=2$, men ingen bunnpunkt.

c)

$\begin{array}{rl}(-5x^2{e}^{-x}-10x{e}^{-x}-10e^{-x}+C{)}^{\prime }& =(-5x^2{e}^{-x}{)}^{\prime }-(10x{e}^{-x}{)}^{\prime }-(10e^{-x}{)}^{\prime }+C^{\prime }\\ & =-10x{e}^{-x}+5x^2{e}^{-x}-10e^{-x}+10x{e}^{-x}+10e^{-x}+0\\ & =5x^2{e}^{-x}\\ & =f(x)\end{array}$

d)

$\underset{a\to \mathrm{\infty }}{lim}{\int }_0^{a}f(x)dx=\underset{a\to \mathrm{\infty }}{lim}[-5x^2{e}^{-x}-10x{e}^{-x}-10e^{-x}{]}_0^a=\underset{a\to \mathrm{\infty }}{lim}-5a^2{e}^{-a}-10a{e}^{-a}-10e^{-a}+10$

Fra det som er oppgitt i oppgaven vil de tre første leddene gå mot $0$, så det eneste som gjenstår er det siste leddet, altså er $\underset{a\to \mathrm{\infty }}{lim}{\int }_0^{a}f(x)dx=10$