1P 2014 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (5 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://www.matematikk.net/matteprat/download/file.php?id=281 Alternativ løsning | *[http://www.matematikk.net/matteprat/download/file.php?id=281 Alternativ løsning (pdf)] | ||
*[http://ndla.no/nb/node/140140?fag=55 Alternativ løsning fra NDLA] | |||
=Del 1= | =Del 1= | ||
| Linje 86: | Linje 87: | ||
'''d)''' | '''d)''' | ||
Avtale 1: P og A er ikke hverken proporsjonale eller omvendt proporsjonale størrelser ettersom det er en funksjon med formen ax + b. Hvis den skulle vært omvendt proporsjonal hadde det ikke vært en rett linje, og hvis den skulle være proporsjonal hadde den ikke hatt et konstantledd. | Avtale 1: P og A er ikke hverken proporsjonale eller omvendt proporsjonale størrelser ettersom det er en funksjon med formen ax + b. Hvis den skulle vært omvendt proporsjonal hadde det ikke vært en rett linje, og hvis den skulle være proporsjonal hadde den ikke hatt et konstantledd. | ||
$P= \frac{20A+160}{A} \\P= 20 + frac{160}{A} | $P= \frac{20A+160}{A} \\P= 20 + \frac{160}{A}$ | ||
Avtale 2: P og A er omvendt proporsjonale størrelser ettersom $P = \frac{400}{A} \\ AP = 400 $ | Avtale 2: P og A er omvendt proporsjonale størrelser ettersom $P = \frac{400}{A} \\ AP = 400 $ | ||
| Linje 131: | Linje 132: | ||
'''a)''' | '''a)''' | ||
Kilopris 1990:$\frac{31kr}{600g} \cdot 1000g = 51, | Kilopris 1990:$\frac{31kr}{600g} \cdot 1000g = 51,67$ kr | ||
Kilopris 2012:$\frac{24kr}{350g} \cdot 1000g = 68, | Kilopris 2012:$\frac{24kr}{350g} \cdot 1000g = 68,57$ kr | ||
'''b)''' | '''b)''' | ||
Endring: $68, | Endring: $68,57kr - 51,67kr = 16,90kr$ | ||
Prosentvis endring: $\frac{16, | Prosentvis endring: $\frac{16,90kr}{51,667kr}=0,327 = 32,7\percent$ | ||
'''Alternativ utregning: ''' | '''Alternativ utregning: ''' | ||
Vekstfaktor: $\frac{68, | Vekstfaktor: $\frac{68,57kr}{51,67kr}=1,33$ | ||
Prosentfaktor: $1, | Prosentfaktor: $1,33 - 1 = 0,33$ | ||
Prosentvis endring: $0, | Prosentvis endring: $0,33 = 33\percent$ | ||
'''c)''' | '''c)''' | ||
$\frac{51, | $\frac{51,67kr}{83,7}=\frac{x}{131,4} \\ | ||
x = \frac{51, | x = \frac{51,67kr \cdot 131,4}{83,7} = 81,11kr$ | ||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 197: | Linje 198: | ||
'''b)''' | '''b)''' | ||
Bruker pytagoras til å finne lengden på stigen til | Bruker pytagoras til å finne lengden på stigen til Grete: $\sqrt{(220cm)^2 + (80cm)^2}=234cm$ | ||
Forhold mellom lengden til stigen og hvor langt stigen går opp på veggen: $\frac{234cm}{220cm}=\frac{\sqrt{137}}{11}$ | Forhold mellom lengden til stigen og hvor langt stigen går opp på veggen: $\frac{234cm}{220cm}=\frac{\sqrt{137}}{11}$ | ||
Siste sideversjon per 21. sep. 2015 kl. 13:35
Del 1
Oppgave 1
$\frac{1}{50} = \frac{6 mm}{x} \\ x= 6mm \cdot 50 = 300mm = 30cm$
Feilen vil bli 30cm i virkeligheten.
Oppgave 2
$617L \approx 600L \\ 15,3L \approx 15L \\ 600L : 15L = 40 $
Du trenger omtrent 40 kanner.
Oppgave 3
a) $\frac{(x+4) \cdot 3}{2}=9\\ \frac{3x+12}{2}=9\\ 3x+12=18\\ 3x=6 \\ x=2$
b) $\frac{(x+4cm) \cdot 3cm}{2}=9cm^2$
Ligningen er den samme som i oppgave a, derfor er lengden av den andre parallelle siden lik 2cm.
Oppgave 4
$7 200 000 000 \cdot 0.10 = 720 000 000 $
Halvparten av $720 000 000 = 360 000 000 \\ 720 000 000 + 360 000 000 = 1 080 000 000$
Cirka 1,08 milliarder mennesker har ikke tilgang til rent vann.
Alternativ utregning:
$7,2 \cdot 10^9 \cdot 1,5 \cdot 10^{-1} = 10,8 \cdot 10^8 = 1,08 \cdot 10^9$
Oppgave 5
$\frac{100}{500000kr}= \frac{x}{600000kr} \\ x = \frac{100 \cdot 600000kr}{500000kr}=120$
KPI var 120 dette året.
Oppgave 6
Liter saft totalt: $0,2L \cdot 500=100L$
Ren saft: $\frac{1}{10} \cdot 100L = 10L$
Det går 10L ren saft med i 100L ferdigblandet saft.
Oppgave 7
a) $\sqrt{(2,5m)^2 - (1,5m)^2}=\sqrt{6,25m^2 - 2.25m^2}=\sqrt{4m^2}=2m$
b) $A=5m \cdot 2m = 10m^2$
$V_{jord}=10m^2 \cdot 0,1m = 1m^3 = 1000L$
Antall sekker: $\frac{1000L}{35L} = 28,571$
Du trenger 29 sekker.
Alternativ utregning:
$30\cdot35L = 1050L$
Man kan bare trekke fra 35L én gang uten at det går under 1000L. Du trenger derfor 29 sekker.
Oppgave 8
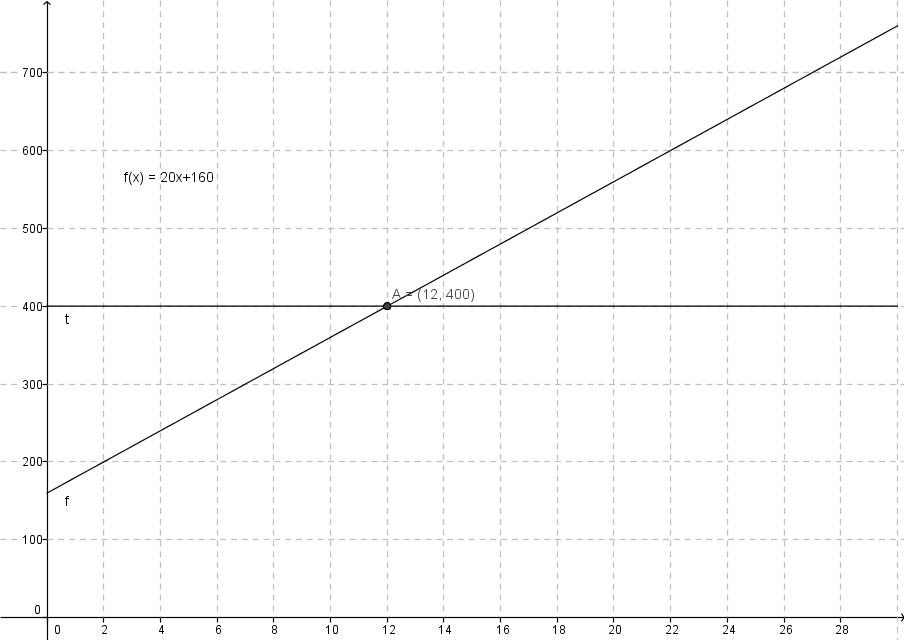
a) Januar: $8 \cdot 20kr + 160kr = 320kr$
Februar: $14 \cdot 20kr + 160kr = 440kr$
b)
c) Lagde en ny funksjon hvor y = 400 i GeoGebra, brukte skjæringsverktøyet og så at grafene skjærte ved x = 12. Hun må altså trene 12 ganger for at avtalene skal være like billig. Derfor må hun trene 13 ganger eller mer for at avtale 2 skal lønne seg.
d) Avtale 1: P og A er ikke hverken proporsjonale eller omvendt proporsjonale størrelser ettersom det er en funksjon med formen ax + b. Hvis den skulle vært omvendt proporsjonal hadde det ikke vært en rett linje, og hvis den skulle være proporsjonal hadde den ikke hatt et konstantledd. $P= \frac{20A+160}{A} \\P= 20 + \frac{160}{A}$
Avtale 2: P og A er omvendt proporsjonale størrelser ettersom $P = \frac{400}{A} \\ AP = 400 $
Oppgave 9
a)
| Gutt | Jente | Sum | |
|---|---|---|---|
| Gjort leksen | $3$ | $6$ | $9$ |
| Ikke gjort leksen | $5$ | $4$ | $9$ |
| Sum | $8$ | $10$ | $18$ |
b) G: Gutt J: jente L: Gjort leksen
P(én gutt og én jente) = $P(J|\bar{L}) \cdot P(G|\bar{L}) + P(G|\bar{L}) \cdot P(J|\bar{L}) = 2 \cdot P(G|\bar{L}) \cdot P(J|\bar{L}) = 2 \cdot \frac{5}{9} \cdot \frac{4}{8}=\frac{5}{9} \cdot \frac{4\cdot2}{8} = \frac{5}{9}$
Del 2
Oppgave 1
a)
Kilopris 1990:$\frac{31kr}{600g} \cdot 1000g = 51,67$ kr
Kilopris 2012:$\frac{24kr}{350g} \cdot 1000g = 68,57$ kr
b)
Endring: $68,57kr - 51,67kr = 16,90kr$
Prosentvis endring: $\frac{16,90kr}{51,667kr}=0,327 = 32,7\percent$
Alternativ utregning:
Vekstfaktor: $\frac{68,57kr}{51,67kr}=1,33$
Prosentfaktor: $1,33 - 1 = 0,33$
Prosentvis endring: $0,33 = 33\percent$
c)
$\frac{51,67kr}{83,7}=\frac{x}{131,4} \\ x = \frac{51,67kr \cdot 131,4}{83,7} = 81,11kr$
Oppgave 2
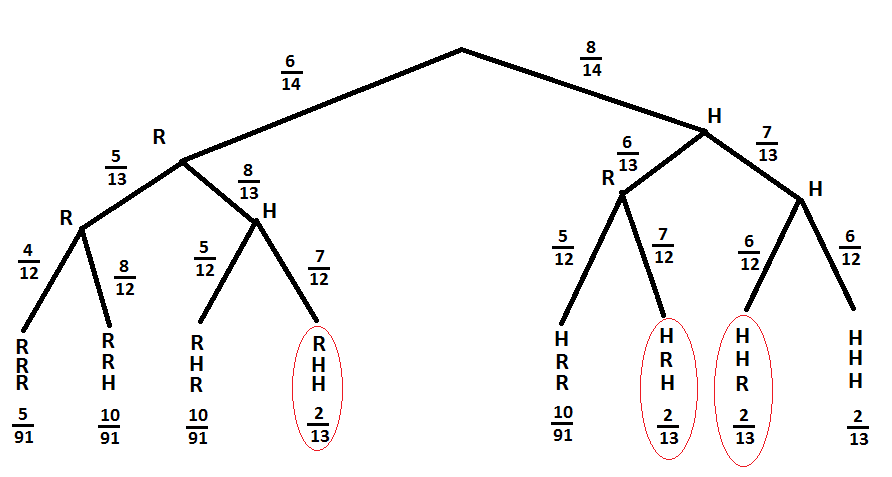
a)
H: Trekker hvit kule
R: Trekker rød kule
b) P(to hvite og én rød) = $P(R, H, H) + P(H, R, H) + P(H, H, R) = 3 \cdot \frac{2}{13}= \frac{6}{13}$
Oppgave 3
a)
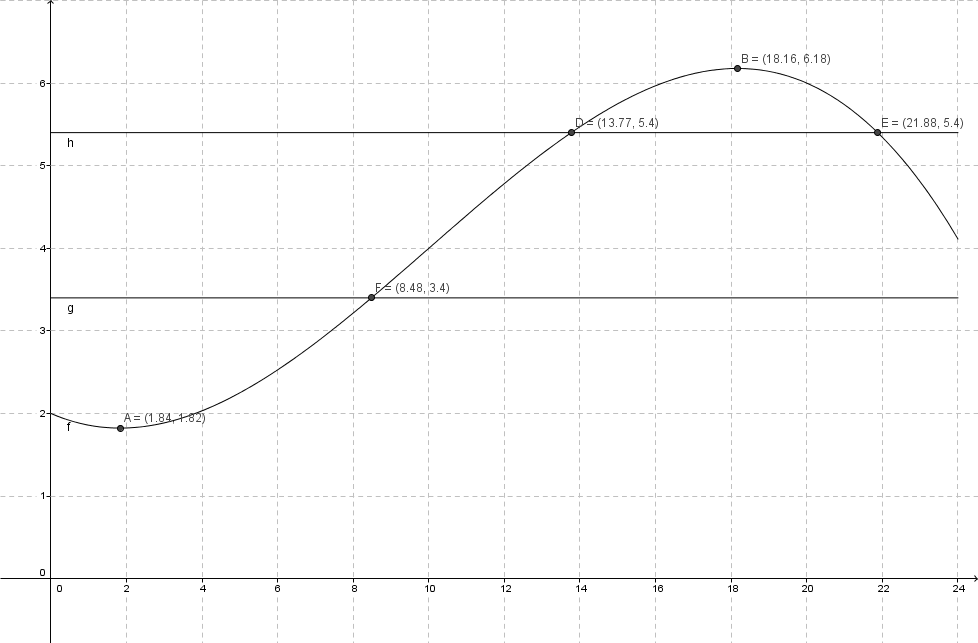
b) La funksjonen inn i GeoGebra og skrev "f(9.75)". Fikk at $f(9,75) = 3,9$.
Vindstyrken var 3,9m/s klokken 09:45.
c) Skrev "Ekstremalpunkt[f]" og fikk punktene A = (1.84, 1.82) og B = (18.16, 6.18).
A er bunnpunktet og det betyr at klokken 01:50 (1,84 timer etter midnatt, $1 + 0,84 \cdot 60$ = 1 time og 50 minutter etter midnatt) var vindstyrken lavest, og den var da 1,82m/s.
B er toppunktet og betyr at klokken 18:10 var vindstyrken høyest, da den var 6,18m/s.
d) La inn funksjonene g(x) = 3,4 og h(x) = 5,4 i GeoGebra, og brukte skjæringsverktøyet til å finne ut når f skar med de nye grafene. Fant at f skar g ved x = 8,48, og skar h ved x = 13,77 og x = 21,88.
Dette betyr at mellom x = 8,48 og x = 13,77 var vindstyrken en "lett bris". Etter x = 13,77 ble vindstyrken høyere, og blir klassifisert som laber bris. Etter x = 21,88 faller vindstyrken under 5,4m/s igjen, og blir lett bris, som varer ut døgnet.
Det var lett bris fra 08:29 til 13:46, og fra 21:53 til 00:00 (ut døgnet).
Oppgave 4
a) $\frac{11}{4} \cdot 80cm = 220cm = 2,2m$
b)
Bruker pytagoras til å finne lengden på stigen til Grete: $\sqrt{(220cm)^2 + (80cm)^2}=234cm$
Forhold mellom lengden til stigen og hvor langt stigen går opp på veggen: $\frac{234cm}{220cm}=\frac{\sqrt{137}}{11}$
$\frac{11}{\sqrt{137}}\cdot 5m = 4,7m$
Alternativ løsning:
$(5m)^2 = (\frac{4}{11x})^2 + x^2 \\ 25m^2 = \frac{16}{121}x^2 + x^2 \\ 25m^2 = \frac{137}{121}x^2 \\ x = \sqrt{\frac{25m^2}{\frac{137}{121}}}=4,7m$
Oppgave 5
a) $246kr \cdot 1,10^5 = 396,2kr$
b) Total vekstfaktor: $1,10^5 = 1,610$
Prosentvis endring: $1,610 - 1 = 0,610 = 61\percent$
Alternativ utregning:
Endring: $396,2kr - 246kr = 150,2kr$
Prosentvis endring: $\frac{150,2kr}{246kr}= 0,610=61\percent$
c)
$x \cdot 1.10^5 = 550kr \\ x = \frac{550kr}{1.10^5} = 341,50kr$
Varen kostet opprinnelig 341,50kr.
Alternativ utregning:
$550kr \cdot 1.10^{-5} = 341,50kr$
Oppgave 6
a)
Lønn: $135kr \cdot 346 = 46710kr$
Beløp over frikort: $46710kr - 39950kr = 6760kr$
Skatt: $0,5 \cdot 6760kr = 3380kr$
Ellinor betalte 3380kr i skatt i 2013.
b)
| Inntekt 2013 | |
| Lån | $94400kr$ |
| Lønn | $43330kr$ |
| Totalt | $137730kr$ |
| Utgifter 2013 | |
| Hybel | $48000kr$ |
| Mat og drikke | $36000kr$ |
| Klær og sko | $14400kr$ |
| Andre utgifter | $25200kr$ |
| Reiser | $10000kr$ |
| Totalt | $133600kr$ |
| Balanse 2013 | |
| Inntekter | $137730kr$ |
| Utgifter | $133600kr$ |
| Overskudd | $4130kr$ |
Oppgave 7
a)
$50cm - 15cm = 35cm$
Dersom blomsterpotten skal være 15m høy, må den ha en omkrets på 35cm.
$r = \frac{35cm}{2\pi} = 5,57cm$
$V = \pi r^2h = \pi \cdot (5,57cm)^2 \cdot 15cm= 1462cm^3$
b)
f(x) er en funksjon for høyden av blomsterpotten hvor x er radius av sylinderen. $50$ representerer det som skal være summen av høyde og omkrets, og $2 \pi x$ er omkretsen av sirkelen i snittet av sylinderen.
g(x) er en funksjon som viser volum av blomsterpotten hvor x igjen er radius. Formelen for volum av en sylinder er $2 \pi r^2 h$, men siden vi vet at $r = x$ og $h = (50-2 \pi x)$, kan vi se at funksjonen er lik formelen for volum av sylinder.
c)
A og C hører til samme blomsterpotte fordi x = 5,3 i begge.
B og D hører til samme blomsterpotte fordi x = 8 i begge.
Vi kan se at ved å sette $r = 5,3cm$ vil vi oppnå det høyeste volum mulig om man følger regelen, og da er volumet $1473,7cm^3$.
Vi kan også se at hvis radius er $8cm$, vil omkretsen bli $50cm$, og $h = 50-50 = 0cm$. Siden $h = 0cm$ ved $r = 8cm$, vil volum også bli $0cm^3$. Man kan altså ikke lage en en blomsterpotte som følger regelen med $8cm$ eller lengre radius.