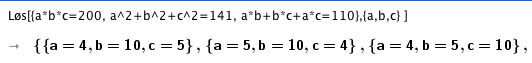S1 eksempeloppgave 2015 vår LØSNING: Forskjell mellom sideversjoner
| (80 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 59: | Linje 59: | ||
===b=== | ===b=== | ||
<math> \left[ \begin{align*}y=x^2-3x-2 \\ y+2 = 2x \end{align*}\right] </math> | |||
<math> \left[ \begin{align*}y=x^2-3x-2 \\ y = 2x -2 \end{align*}\right] </math> | |||
<math> \left[ \begin{align*} 2x-2=x^2-3x-2 \\ x(x-5)=0 \end{align*}\right] </math> | |||
$x =0 \vee x= 5$ | |||
$x=0 \wedge y=-2 \quad \vee \quad x=5 \wedge y=8$ | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | ===a)=== | ||
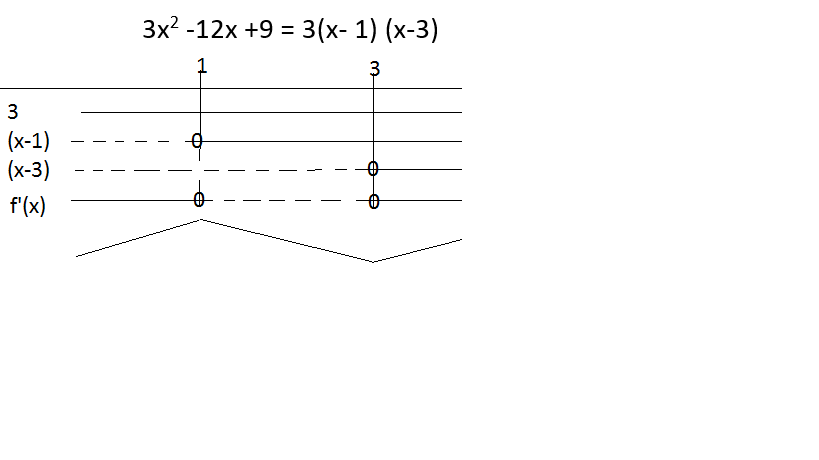
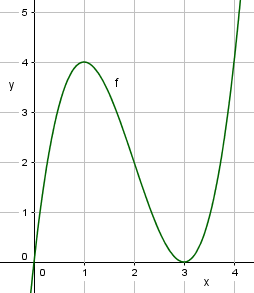
$f(x)= x^3-6x^2+9x \\ f'(x)= 3x^2-12x + 9$ | |||
===b)=== | ===b)=== | ||
[[File:s1-eks-v2015-7b.png]] | |||
[[File:s1-eks-v2015-7b2.png]] | |||
==Oppgave 8== | ==Oppgave 8== | ||
| Linje 72: | Linje 87: | ||
Vi skal bruke definisjonen på den deriverte til å vise dette: | Vi skal bruke definisjonen på den deriverte til å vise dette: | ||
$f´(x) = lim_{\ | $f´(x) = lim_{\Delta x \rightarrow 0} \frac{f(x+ \Delta x) - f(x)}{\Delta x} \\ =lim_{\Delta x \rightarrow 0} \frac{(x+\Delta x)^2 + 2(x+ \Delta x)-x^2-2x}{\Delta x}\\ =lim_{\Delta x \rightarrow 0} \frac{x^2+ 2x \Delta x + ( \Delta x)^2+2x +2 \Delta x -x^2-2x}{\Delta x}\\ =lim_{\Delta x \rightarrow 0} \frac{ \Delta x ( 2x+ \Delta x +2)}{\Delta x} \\= lim_{\Delta x \rightarrow 0} 2x+ \Delta x +2 \\ = 2x+2$ | ||
==Oppgave 9== | ==Oppgave 9== | ||
1) Galt, fordi x= -3 og x=-2 er en løsning av likningen. | |||
2) Riktig, fordi dersom x=-2 så er likningen riktig. | |||
3) Feil. Likningen har også løsning x = -3, følger også av 1). | |||
==Oppgave 10== | ==Oppgave 10== | ||
TREKANTTALL | |||
===a)=== | |||
{| width="auto" | |||
|n | |||
|$a_n$ | |||
|$a_n$ | |||
|$s_n$ | |||
|$s_n$ | |||
|- | |||
|1 | |||
|1 | |||
|$\binom{2}{2}$ | |||
|1 | |||
|$\binom{3}{3}$ | |||
|- | |||
|2 | |||
|3 | |||
|$\binom{3}{2}$ | |||
|4 | |||
|$\binom{4}{3}$ | |||
|- | |||
|3 | |||
|6 | |||
|$\binom{4}{2}$ | |||
|10 | |||
|$\binom{5}{3}$ | |||
|- | |||
|4 | |||
|10 | |||
|$\binom{5}{2}$ | |||
|20 | |||
|$\binom{6}{3}$ | |||
|- | |||
|5 | |||
|15 | |||
|$\binom{6}{2}$ | |||
|35 | |||
|$\binom{7}{3}$ | |||
|} | |||
===b)=== | |||
$a_n =\binom{n+1}{2} \\ S_n = \binom{n+2}{3}$ | |||
==Oppgave 11== | ==Oppgave 11== | ||
Antall gb lagringsplass til minnepinne type 1: a | |||
Antall gb lagringsplass til minnepinne type 2: b | |||
Løser likningsettet: | |||
$a+3b=100$ | |||
$2a+4b=144$ | |||
$2(a+2b)=2\cdot72$ | |||
$(a+3b)-(a+2b)=100-72$ | |||
$b=28$ | |||
$a=100-3b=100-3\cdot28=100-84=16$ | |||
Minnepinne type 1 har en lagringsplass på 16 Gb. | |||
Minnepinne type 2 har en lagringsplass på 28 Gb. | |||
==Oppgave 12== | ==Oppgave 12== | ||
[[File:s1-eks-v2015-12.png]] | |||
==Oppgave 13== | ==Oppgave 13== | ||
[[File:s1-eks-v2015-13.png]] | |||
==DEL TO (NB: Nå kun to timer)== | |||
==Oppgave 1== | |||
===a)=== | |||
Volumet av det rette prismet er 200. Man får da: | |||
$abc= 200$ | |||
for å finne lengden av d må man først finne lenden av diagonalen i ab planet. Man bruker Pytagoras to ganger og får da | |||
$a^2+b^2+c^2 = 141$ | |||
To og to sider har samme areal, summen av de tre forskjellige sidene blir halvparten av prismes overflate: | |||
$ab+bc+ac=110$ | |||
===b)=== | |||
[[File:s1-v2015-eks-1a2.png]] | |||
[[File:s1-v2015-eks-1a22.png]] | |||
Man observere at a, b og c får alle kombinasjoner av lengdene 4, 5 og 10. | |||
==Oppgave 2== | |||
===a)=== | |||
[[File:s1-eksempel-2abc.png]] | |||
===b)=== | |||
Se figuren i a. | |||
===c)=== | |||
Overskuddet blir størst ved 313 brød. Det er da på 2268 kroner. | |||
==Oppgave 3== | |||
===a)=== | |||
Sannsynligheten er den samme i alle delforsøk. | |||
To alternativer, rett eller ikke rett. | |||
Delforsøkene er uavhengige av hverandre. | |||
===b)=== | |||
[[File:s1-eksempel-3b.png]] | |||
Det er 17,7% sannsynlig at man får akkurat fem rette svar. | |||
===c)=== | |||
[[File: s1-eksempel-3c.png]] | |||
Det er ca 37% sannsynlig at man får minst 5 rette svar. | |||
==Oppgave 4== | |||
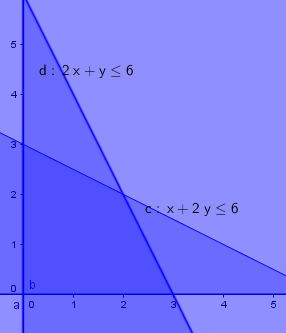
===a)=== | |||
x er tonn grus, og y er tonn pukk. | |||
Han kan maksimalt importere 900 tonn grus, derfor | |||
$0 \leq x \leq 900$ | |||
Han kan maksimalt importere 1000 tonn pukk, derfor | |||
$0 \leq x \leq 1000$ | |||
Han kan bare importere 1000 kubikkmeter totalt, derfor: | |||
$\frac{x}{1,6} + \frac{y}{1,36} \leq 1000 \\ \frac {1,6 \cdot 1,36 \cdot x}{1,6} + \frac{1,6 \cdot 1,36 \cdot y }{1,36} \leq 1000 \cdot 1,6 \cdot 1,36 \\ 1,36x + 1,60y \leq 2176$ | |||
===b)=== | |||
$F(x,y)= 74x + 106y$ | |||
Utsalgsprisen for pukk er 106 kroner per tonn. | |||
===c)=== | |||
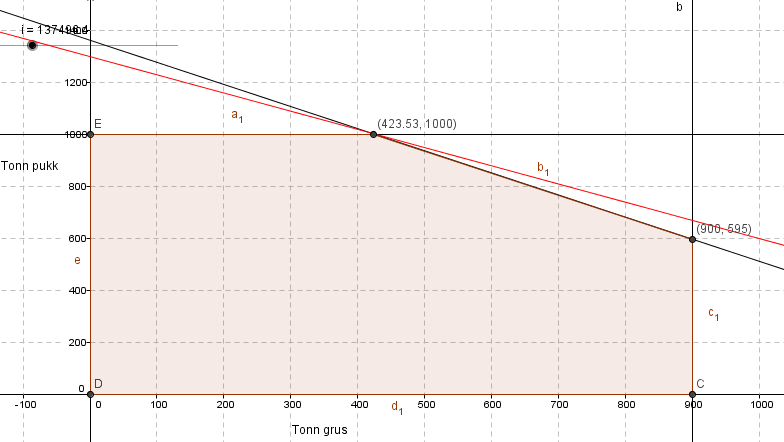
[[File:s1-eksempel-4c.png]] | |||
For å få størst mulig inntekter bør han selge 423,5 tonn grus og 1000 tonn pukk. | |||
Inntekten blir da $F(423,5, 1000) = 74 \cdot 423,5 + 106 \cdot 1000 = 137 339$ kroner. | |||
==Oppgave 5== | |||
===a)=== | |||
Sidene i boksens grunnflate blir a-2x. Arealet av grunnflaten blir da $(a-2x)^2$ . Multipliserer vi arealet av grunnflaten med høyden av esken, som er x får vi: | |||
$a>0 \wedge x< \frac a2$ | |||
$ V(x)= (a-2x)^2 \cdot x $ | |||
===b)=== | |||
$ V(x)= (a-2x)^2 \cdot x \\ V(x)= (a^2-4ax+4x^2) \cdot x \\ V(x)= 4x^3 - 4ax^2 +a^2x \\ V'(x) = 12x^2 - 8ax +a^2 $ | |||
$V'(x)=0 \\ 12x^2-8ax+a^2=0 \\ x= \frac{8a \pm \sqrt{64a^2-4 \cdot 12 \cdot a^2}}{24} \\ x= \frac{8a \pm \sqrt{16a^2}}{24} \\ x= \frac{8a \pm 4a}{24} \\ x= \frac a2 \vee x= \frac a6$ | |||
Størst volum får esken når x er en sjettedels a. | |||
==Oppgave 6== | |||
$f(x)= ax^3-bx-2 \\ f'(x)= 3ax^2-b \\ 0 = 12a -b \\ 2 = 3a-b $ | |||
De to siste linjene benytter informasjonen om den deriverte i x = 2 og x = 1. | |||
$f'(2)= 0 \\ 0= 12a-b \\ f'(1)=2 \\ 2= 3a-b$ | |||
Løser likningsettet: | |||
$b=12a\\ 2= 3a - 12a \\ a= - \frac 29 \\ b= - \frac{24}{9} $ | |||
Funksjonen blir da: | |||
$f(x)= -\frac 29 x^3 + \frac {24}{9}x-2$ | |||
Siste sideversjon per 28. sep. 2015 kl. 05:48
DEL EN ( NB: Nå tre timer)
Oppgave 1
a)
$f(x)=3x^2-4x+2 \\ f ´(x)= 6x-4$
b)
$g(x)= 3x^3-3 \\ g ´(x)= 9x^2 \\ g ´(2) = 9 \cdot 4 = 36$
Oppgave 2
a)
$\frac{2^{-1}\cdot a \cdot b^{-1}}{4^{-1} \cdot a^{-2} \cdot b^2} = \frac{4 a^3}{2b^3} = 2 (\frac ab)^3$
b)
$lg(a^2b)+lg(ab^2)+lb(\frac{a}{b^3}) = 2lga+ lgb + lga + 2lgb + lga - 3lgb = 4lga$
c)
$ \frac{3a^2-75}{6a+30} = \frac{3(a+5)(a-5)}{6(a+5)}= \frac{a-5}{2}$
Oppgave 3
a)
$\frac{61^2-39^2}{51^2-49^2} = \\ \frac{(61+39)(61-39)}{(51+49)(51-49)} =\\ \frac{100 \cdot 22}{100 \cdot 2} =11 $
b)
$1997 \cdot 2003 - 1993 \cdot 2007 = \\ (2000 - 3)(2000 + 3) - ( 2000 - 7)( 2000+7) \\ 2000^2 -3^2 - 2000^2 + 7^2 \\ -9 + 49 = 40$
Oppgave 4
$f(x) = g(x) \\ x^2-x-2 = x+1 \\ x^2-2x-3 = 0 \\ x= \frac{2 \pm \sqrt{4+12}}{2} \\ x=-1 \vee x= 3 \\ g(-1)=0 \wedge g(3)= 4 \\$
Skjæringspunktene mellom f og g er (-1, 0) og (3,4)
Oppgave 5
a)
$3x^2=18-3x \\ 3x^2+3x-18=0 \\ x^2 +x -6 =0 \\ x= \frac{-1 \pm \sqrt{1+24}}{2} \\ x= \frac{-1 \pm 5}{2} \\ x= -3 \vee x=2$
b)
$3 \cdot 2^x =24 \\ 2^x= 8 \\ 2^x=2^3 \\ x=3$
c)
$3^8+3^8+3^8+3^8 +3^8+3^8+3^8+3^8+3^8 = 3^x\\ 9 \cdot 3^8= 3^x \\ 3^{10} = 3^x \\ 10 lg3 = x lg3 \\ x=10$
Oppgave 6
a)
$ y= a \cdot b^x \\ b^x= \frac ya \\x lgb = lg (\frac ya) \\ x = \frac{ lg(\frac ya) }{lgb} $
b
<math> \left[ \begin{align*}y=x^2-3x-2 \\ y+2 = 2x \end{align*}\right] </math>
<math> \left[ \begin{align*}y=x^2-3x-2 \\ y = 2x -2 \end{align*}\right] </math>
<math> \left[ \begin{align*} 2x-2=x^2-3x-2 \\ x(x-5)=0 \end{align*}\right] </math>
$x =0 \vee x= 5$
$x=0 \wedge y=-2 \quad \vee \quad x=5 \wedge y=8$
Oppgave 7
a)
$f(x)= x^3-6x^2+9x \\ f'(x)= 3x^2-12x + 9$
b)
Oppgave 8
$f(x)= x^2+2x \quad D_f= \R \\ f ´(x) = 2x+2$
Vi skal bruke definisjonen på den deriverte til å vise dette:
$f´(x) = lim_{\Delta x \rightarrow 0} \frac{f(x+ \Delta x) - f(x)}{\Delta x} \\ =lim_{\Delta x \rightarrow 0} \frac{(x+\Delta x)^2 + 2(x+ \Delta x)-x^2-2x}{\Delta x}\\ =lim_{\Delta x \rightarrow 0} \frac{x^2+ 2x \Delta x + ( \Delta x)^2+2x +2 \Delta x -x^2-2x}{\Delta x}\\ =lim_{\Delta x \rightarrow 0} \frac{ \Delta x ( 2x+ \Delta x +2)}{\Delta x} \\= lim_{\Delta x \rightarrow 0} 2x+ \Delta x +2 \\ = 2x+2$
Oppgave 9
1) Galt, fordi x= -3 og x=-2 er en løsning av likningen.
2) Riktig, fordi dersom x=-2 så er likningen riktig.
3) Feil. Likningen har også løsning x = -3, følger også av 1).
Oppgave 10
TREKANTTALL
a)
| n | $a_n$ | $a_n$ | $s_n$ | $s_n$ |
| 1 | 1 | $\binom{2}{2}$ | 1 | $\binom{3}{3}$ |
| 2 | 3 | $\binom{3}{2}$ | 4 | $\binom{4}{3}$ |
| 3 | 6 | $\binom{4}{2}$ | 10 | $\binom{5}{3}$ |
| 4 | 10 | $\binom{5}{2}$ | 20 | $\binom{6}{3}$ |
| 5 | 15 | $\binom{6}{2}$ | 35 | $\binom{7}{3}$ |
b)
$a_n =\binom{n+1}{2} \\ S_n = \binom{n+2}{3}$
Oppgave 11
Antall gb lagringsplass til minnepinne type 1: a
Antall gb lagringsplass til minnepinne type 2: b
Løser likningsettet:
$a+3b=100$
$2a+4b=144$
$2(a+2b)=2\cdot72$
$(a+3b)-(a+2b)=100-72$
$b=28$
$a=100-3b=100-3\cdot28=100-84=16$
Minnepinne type 1 har en lagringsplass på 16 Gb.
Minnepinne type 2 har en lagringsplass på 28 Gb.
Oppgave 12
Oppgave 13
DEL TO (NB: Nå kun to timer)
Oppgave 1
a)
Volumet av det rette prismet er 200. Man får da:
$abc= 200$
for å finne lengden av d må man først finne lenden av diagonalen i ab planet. Man bruker Pytagoras to ganger og får da
$a^2+b^2+c^2 = 141$
To og to sider har samme areal, summen av de tre forskjellige sidene blir halvparten av prismes overflate:
$ab+bc+ac=110$
b)
Man observere at a, b og c får alle kombinasjoner av lengdene 4, 5 og 10.
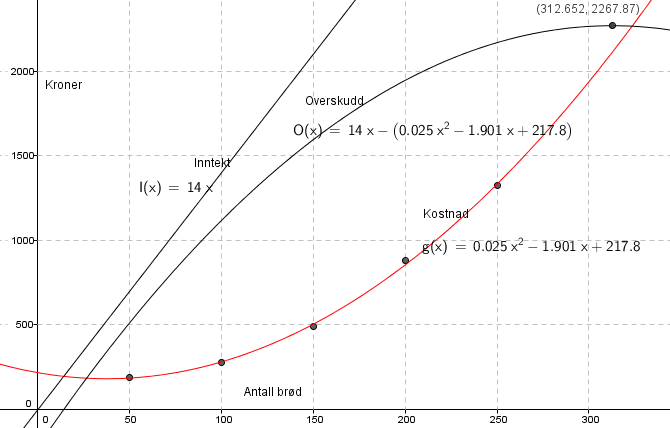
Oppgave 2
a)
b)
Se figuren i a.
c)
Overskuddet blir størst ved 313 brød. Det er da på 2268 kroner.
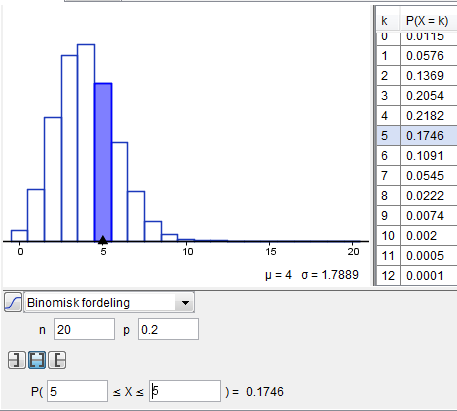
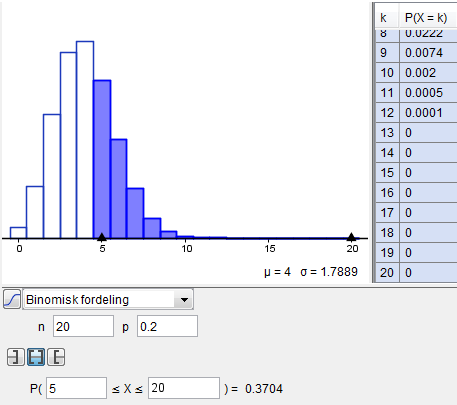
Oppgave 3
a)
Sannsynligheten er den samme i alle delforsøk.
To alternativer, rett eller ikke rett.
Delforsøkene er uavhengige av hverandre.
b)
Det er 17,7% sannsynlig at man får akkurat fem rette svar.
c)
Det er ca 37% sannsynlig at man får minst 5 rette svar.
Oppgave 4
a)
x er tonn grus, og y er tonn pukk.
Han kan maksimalt importere 900 tonn grus, derfor
$0 \leq x \leq 900$
Han kan maksimalt importere 1000 tonn pukk, derfor
$0 \leq x \leq 1000$
Han kan bare importere 1000 kubikkmeter totalt, derfor:
$\frac{x}{1,6} + \frac{y}{1,36} \leq 1000 \\ \frac {1,6 \cdot 1,36 \cdot x}{1,6} + \frac{1,6 \cdot 1,36 \cdot y }{1,36} \leq 1000 \cdot 1,6 \cdot 1,36 \\ 1,36x + 1,60y \leq 2176$
b)
$F(x,y)= 74x + 106y$
Utsalgsprisen for pukk er 106 kroner per tonn.
c)
For å få størst mulig inntekter bør han selge 423,5 tonn grus og 1000 tonn pukk.
Inntekten blir da $F(423,5, 1000) = 74 \cdot 423,5 + 106 \cdot 1000 = 137 339$ kroner.
Oppgave 5
a)
Sidene i boksens grunnflate blir a-2x. Arealet av grunnflaten blir da $(a-2x)^2$ . Multipliserer vi arealet av grunnflaten med høyden av esken, som er x får vi:
$a>0 \wedge x< \frac a2$
$ V(x)= (a-2x)^2 \cdot x $
b)
$ V(x)= (a-2x)^2 \cdot x \\ V(x)= (a^2-4ax+4x^2) \cdot x \\ V(x)= 4x^3 - 4ax^2 +a^2x \\ V'(x) = 12x^2 - 8ax +a^2 $
$V'(x)=0 \\ 12x^2-8ax+a^2=0 \\ x= \frac{8a \pm \sqrt{64a^2-4 \cdot 12 \cdot a^2}}{24} \\ x= \frac{8a \pm \sqrt{16a^2}}{24} \\ x= \frac{8a \pm 4a}{24} \\ x= \frac a2 \vee x= \frac a6$
Størst volum får esken når x er en sjettedels a.
Oppgave 6
$f(x)= ax^3-bx-2 \\ f'(x)= 3ax^2-b \\ 0 = 12a -b \\ 2 = 3a-b $
De to siste linjene benytter informasjonen om den deriverte i x = 2 og x = 1.
$f'(2)= 0 \\ 0= 12a-b \\ f'(1)=2 \\ 2= 3a-b$
Løser likningsettet: $b=12a\\ 2= 3a - 12a \\ a= - \frac 29 \\ b= - \frac{24}{9} $
Funksjonen blir da:
$f(x)= -\frac 29 x^3 + \frac {24}{9}x-2$