1P 2013 vår LØSNING: Forskjell mellom sideversjoner
| (32 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=35168 Diskusjon omkring denne oppgaven] | {{EksLenker|1= | ||
*[http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=35168 Diskusjon omkring denne oppgaven] | |||
[http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=35211 Mer diskusjon omkring denne oppgaven] | *[http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=35211 Mer diskusjon omkring denne oppgaven] | ||
*[http://matematikk.net/res/eksamen/1P/sensur/2013V-FS.pdf Forhåndssensur] | |||
*[http://matematikk.net/res/eksamen/1P/sensur/2013V-S.pdf Sensorveiledning] | |||
*[http://matematikk.net/res/eksamen/1P/sensur/2013V-V.pdf Vurderingsskjema] | |||
*[http://ndla.no/nb/node/127827?fag=55 Løsning fra NDLA] | |||
}} | |||
=Del 1= | =Del 1= | ||
==Oppgave 1== | ==Oppgave 1== | ||
$15 \cdot 2 kr + 2,5 \cdot | Bruker overslagsregning. | ||
$15 \cdot 2 kr + 2,5 \cdot 10 kr + 0,5 \cdot 90 kr + 0,2 \cdot 200 kr = 30 kr + 25 kr + 45 kr + 40 kr = 140 kr$ | |||
Husk: på oppgaver der det står at man skal gjøre overslag vil man '''ikke''' få full uttelling dersom man allikevel regner helt nøyaktig. | |||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 59: | Linje 68: | ||
'''a)''' | '''a)''' | ||
Ris: $\frac{10}{3} \cdot 1,5 dl = 5,0 | Ris: $\frac{10}{3} \cdot 1,5 dl = 5,0 dL$ | ||
Vann: $\frac{10}{3} \cdot 3,0 dl = 10,0 | Vann: $\frac{10}{3} \cdot 3,0 dl = 10,0 dL = 1,0 L$ | ||
Melk: $\frac{10}{3} \cdot 0,75 dl = 2,5 | Melk: $\frac{10}{3} \cdot 0,75 dl = 2,5 L$ | ||
'''b)''' | '''b)''' | ||
$\frac{3}{0,75 L} \cdot 5 L = 20$ | Du kan lage $\frac{3}{0,75 L} \cdot 5 L = 20$ porsjoner | ||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 161: | Linje 170: | ||
'''b)''' | '''b)''' | ||
$\frac {3} {5} \cdot \frac {2} {4} + \frac {2} {5} \cdot \frac {1} {4} = \frac {4} {10} = \frac {2} {5}$ | |||
=Del 2= | =Del 2= | ||
==Oppgave 1== | ==Oppgave 1== | ||
'''a)''' | |||
<table width=0> | |||
<tr> | |||
<th>Arbeid</th> | |||
<th>Antall timer</th> | |||
<th>Timelønn</th> | |||
<th>Inntekt</th> | |||
</tr> | |||
<tr> | |||
<td>Vanlig arbeidstid</td> | |||
<td>$150$</td> | |||
<td>$195kr $</td> | |||
<td>$150 \cdot 195kr = 29250 kr$</td> | |||
</tr> | |||
<tr> | |||
<td>Overtid med $50\%$ tillegg</td> | |||
<td>$16$</td> | |||
<td>$195kr \cdot 1,5 = 292,5kr$</td> | |||
<td>$16 \cdot 292,5kr = 4680 kr$</td> | |||
</tr> | |||
<tr> | |||
<td>Overtid med $100\%$ tillegg</td> | |||
<td>$6$</td> | |||
<td>$195kr \cdot 2 = 390kr$</td> | |||
<td>$6 \cdot 390kr = 2340 kr$</td> | |||
</tr> | |||
</table> | |||
Bruttolønna er $29250 + 4680 + 2340 = 36270kr$ | |||
'''b)''' | |||
$36270kr \cdot 0,02 = 725,40 kr$ | |||
Ole betalte 725,40 kr til pensjonskassen. | |||
'''c)''' | |||
Grunnlag for skattetrekk er $\text{Bruttolønn} - \text{Pensjonstrekk} = 36270-725.40=35544.60 kr$ | |||
Finner $36\%$ av $35544.60 kr $. $0,36 \cdot 35544.60 =12796 kr $ | |||
$35544.60 - 12796 = 22748.54 kr$ | |||
Ole fikk 22748.54 kr utbetalt denne måneden. | |||
'''d)''' | |||
Antar at Ole må betale skatt på pengene han får utbetalt. Skatten er på $36\%$. | |||
Timelønn med 50% tillegg: 292,5 kr (fra deloppgave a) | |||
Utbetalt (lønn etter skatt): 5045 kr | |||
Bruttolønn (lønn før skatt): ${5045 kr \over (1 - 0.36)} = 7882,81 kr$ | |||
${7882,81 kr \over 292,5 kr} = 26,94 \approx 27$ | |||
Ole jobbet 27 timer med prosjektet. | |||
'''Alternativ utregning (der vi antar at Ole ikke betaler skatt av disse pengene)''' | |||
${5045 kr \over 292,5 kr} = 17,24$ | |||
Ole jobbet 17 timer og ett kvarter (15 minutter) med prosjektet. | |||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 210: | Linje 287: | ||
==Oppgave 3== | ==Oppgave 3== | ||
'''a)''' | |||
$2,00m \cdot 0,70m \cdot 1,00m = 1,4 m^3$ | |||
Fordi $1 m^3 = 1000L$ så inneholder beholderen $1400$ liter. | |||
'''b)''' | |||
Finner først hvor mye det har regnet: | |||
Takets areal: $70 m^2$ | |||
Mengde nedbør: $12mm = 12 mm \cdot 0,001 \frac{m}{mm} = 0,012 m$ | |||
Mengde nedbør som falt på taket: $70 m^2 \cdot 0,012 m = 0,84 m^3$ | |||
Grunnflate i beholderen: $2.00m \cdot 0,70m = 1,4m^2$ | |||
${{0,84 m^3 }\over {1,4 m^2}} = 0,6 m$ | |||
Vannet står 0,6 meter høyt i beholderen. | |||
'''c)''' | |||
Hvor mye mer vann det er i tanken: $ (0,85m - 0,10m) \cdot 1,4 m^2 = 1,05 m^3$ | |||
Takets areal: $70 m^2$ | |||
${1,05 m^3 \over 70 m^2} = 0,015 m = 15mm$ | |||
Det har regnet 15mm mens familien var borte. | |||
==Oppgave 4== | ==Oppgave 4== | ||
| Linje 245: | Linje 357: | ||
Antall år: $1998 - 1994 = 4 $ | Antall år: $1998 - 1994 = 4 $ | ||
Endring i antall hjort: $788 - | Endring i antall hjort: $524 - 788 = -264$ | ||
Endring per år: $\frac {264}{4} = 66$ | Endring per år: $\frac {-264}{4} = -66$ | ||
Bestanden av hjort minsker i gjennomsnitt med 66 dyr per år i perioden $1994$ til $1998$. | Bestanden av hjort minsker i gjennomsnitt med 66 dyr per år i perioden $1994$ til $1998$. | ||
==Oppgave 5== | ==Oppgave 5== | ||
'''a)''' | |||
Fordi alle terminbeløpene er like store, så er dette et annuitetslån. | |||
'''b)''' | |||
Legger sammen alle avdragene for å finne det totale lånebeløpet: | |||
$6396 + 7010 + 7683 + 8420 +9229 + 10115 + 11086 + 12150 +13316 + 14595= 100000 kr$ | |||
Det totale lånebeløpet er 100000kr. | |||
'''c)''' | |||
Første termin (som er første år) betaler han renter på 100000 kr. Rentene er 9600kr. | |||
${9600 \over 100000 } = 0,096 = 9,6 \%$ | |||
Renta er $9,6 \%$ per år. | |||
==Oppgave 6== | ==Oppgave 6== | ||
'''a)''' | |||
$V = \frac13 \pi r^2 h = \frac 13 \pi \cdot r^2 \cdot \frac 23 \cdot r= \frac13 \pi \cdot (1,35\,m)^2 \cdot 0,66 \cdot 1,35\,m \approx 1,72\,m^3$ | |||
'''b)''' | |||
Løser likningen: | |||
$ V = \frac13 \pi \cdot r^2 \cdot h \\ V= \frac 13 \pi \cdot \frac 94 h^2 \cdot h \\ h = \sqrt[3]{\frac{8,0\,m^3 \cdot 4}{3 \pi}} \\ \approx 1,5 m$ | |||
En kjegle med volum 8 kubikkmeter vil ha en høyde på ca 1,5 meter. | |||
Siste sideversjon per 19. nov. 2016 kl. 18:41
Del 1
Oppgave 1
Bruker overslagsregning.
$15 \cdot 2 kr + 2,5 \cdot 10 kr + 0,5 \cdot 90 kr + 0,2 \cdot 200 kr = 30 kr + 25 kr + 45 kr + 40 kr = 140 kr$
Husk: på oppgaver der det står at man skal gjøre overslag vil man ikke få full uttelling dersom man allikevel regner helt nøyaktig.
Oppgave 2
210kr er 70% av originalprisen.
Går veien om 1% : ${210kr \over 70} = 3 kr$
$3kr \cdot 100 = 300 kr$
Før prisen ble satt ned kostet varen 300 kr.
Alternativ utregning:
Vekstfaktor når noe er satt ned med 30% er $1-0,30 = 0,70$
${210 kr \over 0,70} = 300 kr$
Oppgave 3
I basisåret er indeksen 100.
Indeksen i dag er 110, det betyr at varen har økt i verdi med 10%
10% av 150kr er $150kr : 10 = 15kr$
Prisen på varen har dermed økt med 15kr. $150kr + 15kr = 165kr $
Alternativ løsning $pris_{2013} = \frac{pris_{basisår} \ indeks_{2013}}{100} = \frac{150 kr \cdot 110}{100} = 1,5 kr\cdot 110 = 165 kr$
Oppgave 4
a)
$\angle B = 180^o - \angle A - \angle C = 180^o -34,1^o - 101,5^o = 44,4^o$
$\angle E = 180^o - \angle D - \angle F = 180^o - 101,5^o - 44,4^o = 34,1^o$
Vi ser nå at alle vinklene i de to trekantantene er like store og har dermed vist at trekantene er formlike.
b)
Formlikhet gir:
$\frac{AC}{DE} = \frac{AB}{EF} \rightarrow AC = \frac{AB \cdot DE}{EF} = \frac{7,0 \cdot 7,0}{9,8} = 5,0$
$\frac{DF}{BC} = \frac{EF}{AB} \rightarrow DF = \frac{EF \cdot BC}{AB} = \frac{9,8 \cdot 4,0}{7,0} = 5,6$
Oppgave 5
a)
Ris: $\frac{10}{3} \cdot 1,5 dl = 5,0 dL$
Vann: $\frac{10}{3} \cdot 3,0 dl = 10,0 dL = 1,0 L$
Melk: $\frac{10}{3} \cdot 0,75 dl = 2,5 L$
b)
Du kan lage $\frac{3}{0,75 L} \cdot 5 L = 20$ porsjoner
Oppgave 6
a)
Halvsirkelens areal: $A_{hs} = \frac12 \cdot \pi r^2 = \frac12 \pi \cdot (1,0 m)^2 = \frac{\pi }{2} cm^2$
Trekantens areal: $A_{t} = \frac12 gh = \frac12 \cdot 3,0m \cdot 1,0m = \frac{3,0}{2} cm^2$
Siden $\frac{\pi}{2} > \frac{3,0}{2}$ kan vi si at halvsirkelen har størst areal.
b)
Halvsirkelens omkrets: $O_{hs} = \frac12 \cdot 2 \pi \cdot r + 2r = \pi \cdot r + 2r = (\pi +2) r \approx 5,14 m$
Må finne lengdene av sidene AC og BC i trekanten først. Fordi trekanten er like beint vil AC = BC, og pytagoras gir:
$AC = BC = \sqrt{h^2 + (\frac12 AB)^2} = \sqrt{(1,0m)^2 + (1,5 m)^2} = \sqrt{1,0 + 2,25} m = \sqrt{3,25}m$=
Trekantens omkrets: $O_t = AB + BC + AC = 3,0 m + \sqrt{3,25}m + \sqrt{3,25}m = (3 + 2 \sqrt{3,25}) m$
Tallet $2 \sqrt{3,25}$ er større enn $2,14$, og derfor kan vi slutte at omkretsen av trekanten er størst.
Oppgave 7
a)
Etter åtte dager: $60 L - 5,0 L \cdot 8 = 20 L$
Løser likningen:
60 - 5x = 0
x = 12
Tom tank etter: 12 dager
b)
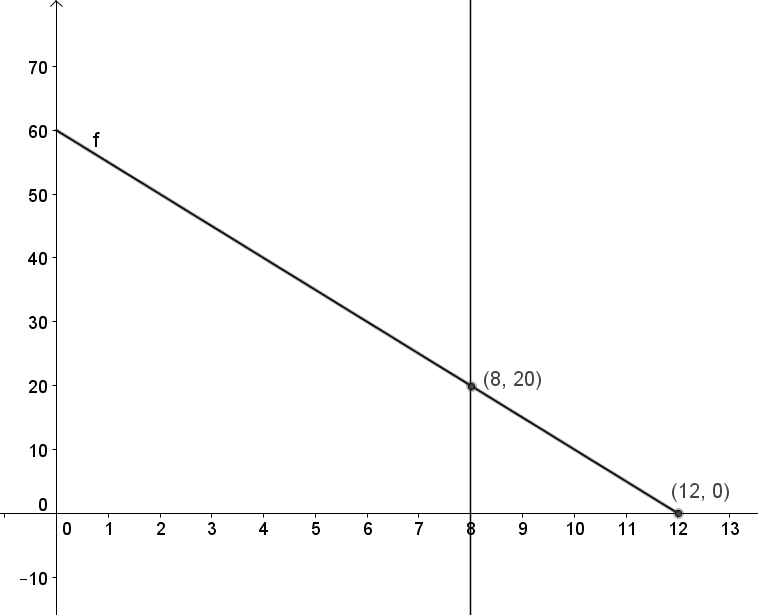
$f(x) = 60 - 5x\,\,\, , \,\,\,x \in[0,12]$
c)
1) Bruker GeoGebra til å tegne grafen til f(x)
2) Tegner linja x = 8, og bruker verktøyet "Skjæring mellom to objekt" og finner skjæringspunktet mellom grafen til f og linja x = 8. Dette gir svaret: Etter 8 dager innholder tanken 20 L
3) Bruker verktøyet "Skjæring mellom to objekt" og finner skjæringspunket mellom x.aksen og grafen til f. Dette gir svaret: Tanken er tom etter 12 dager.
Oppgave 8
a)
Antall kuler: $5$
Antall røde kuler: $3$
Antall blå kuler: $5-3=2$
$P(\text{to røde kuler}) = \frac{3}{5} \cdot \frac{2}{4} = \frac{3 \cdot 2}{5 \cdot 4} = \frac{6}{20} = \frac{3}{10}= 0.3$
Sannsynligheten for å trekke to røde kuler er $0.3$
b)
$P(\text{trekker to røde kuler}) = 0.3$ (fra deloppgave a)
$P(\text{trekker to blå kuler}) = \frac{2}{5} \cdot \frac{1}{4} = \frac{2 \cdot 1}{5 \cdot 4} = \frac{2}{20} = \frac{1}{10}= 0.1$
$P(\text{trekker to kuler i samme farge}) = P(\text{trekker to røde kuler}) + P(\text{trekker to blå kuler}) = 0,3 + 0,1 = 0,4$
Sannsynligheten for at de to kulene han trekker har samme farge er $0,4 = 40\%$
Alternativ utregning
a)
$\frac{ {3 \choose 2} } { {5 \choose 2} } = \frac{3}{10}$
b)
$\frac{ {3 \choose 2} } { {5 \choose 2} } + \frac{ { 2\choose 2} } { {5 \choose 2} } = \frac{4}{10} = \frac {2} {5}$
Alternativ utregning
a)
$\frac {3} {5} \cdot \frac {2} {4} = \frac {3} {10}$
b)
$\frac {3} {5} \cdot \frac {2} {4} + \frac {2} {5} \cdot \frac {1} {4} = \frac {4} {10} = \frac {2} {5}$
Del 2
Oppgave 1
a)
| Arbeid | Antall timer | Timelønn | Inntekt |
|---|---|---|---|
| Vanlig arbeidstid | $150$ | $195kr $ | $150 \cdot 195kr = 29250 kr$ |
| Overtid med $50\%$ tillegg | $16$ | $195kr \cdot 1,5 = 292,5kr$ | $16 \cdot 292,5kr = 4680 kr$ |
| Overtid med $100\%$ tillegg | $6$ | $195kr \cdot 2 = 390kr$ | $6 \cdot 390kr = 2340 kr$ |
Bruttolønna er $29250 + 4680 + 2340 = 36270kr$
b)
$36270kr \cdot 0,02 = 725,40 kr$
Ole betalte 725,40 kr til pensjonskassen.
c)
Grunnlag for skattetrekk er $\text{Bruttolønn} - \text{Pensjonstrekk} = 36270-725.40=35544.60 kr$
Finner $36\%$ av $35544.60 kr $. $0,36 \cdot 35544.60 =12796 kr $
$35544.60 - 12796 = 22748.54 kr$
Ole fikk 22748.54 kr utbetalt denne måneden.
d)
Antar at Ole må betale skatt på pengene han får utbetalt. Skatten er på $36\%$.
Timelønn med 50% tillegg: 292,5 kr (fra deloppgave a)
Utbetalt (lønn etter skatt): 5045 kr
Bruttolønn (lønn før skatt): ${5045 kr \over (1 - 0.36)} = 7882,81 kr$
${7882,81 kr \over 292,5 kr} = 26,94 \approx 27$
Ole jobbet 27 timer med prosjektet.
Alternativ utregning (der vi antar at Ole ikke betaler skatt av disse pengene)
${5045 kr \over 292,5 kr} = 17,24$
Ole jobbet 17 timer og ett kvarter (15 minutter) med prosjektet.
Oppgave 2
a)
$P(\text{taco til middag}) = \frac{18}{30} = \frac{3}{5} = 0,6$
b)
$P(\text{taco til middag og marsipankake til dessert}) = P(\text{taco til middag}) \cdot P(\text{marsipankake til dessert}) = \frac{18}{30} \cdot \frac{24}{30} = \frac{12}{25} = 0,48$
c)
| Taco | Pizza | Totalt | |
|---|---|---|---|
| Sjokoladekake | 2 | 4 | 6 |
| Marsipankake | 16 | 8 | 24 |
| Totalt | 18 | 12 | 30 |
$P(\text{taco og marsipankake}) = \frac{16}{30} = \frac{8}{15} = 0.53$
Oppgave 3
a)
$2,00m \cdot 0,70m \cdot 1,00m = 1,4 m^3$
Fordi $1 m^3 = 1000L$ så inneholder beholderen $1400$ liter.
b)
Finner først hvor mye det har regnet:
Takets areal: $70 m^2$
Mengde nedbør: $12mm = 12 mm \cdot 0,001 \frac{m}{mm} = 0,012 m$
Mengde nedbør som falt på taket: $70 m^2 \cdot 0,012 m = 0,84 m^3$
Grunnflate i beholderen: $2.00m \cdot 0,70m = 1,4m^2$
${{0,84 m^3 }\over {1,4 m^2}} = 0,6 m$
Vannet står 0,6 meter høyt i beholderen.
c)
Hvor mye mer vann det er i tanken: $ (0,85m - 0,10m) \cdot 1,4 m^2 = 1,05 m^3$
Takets areal: $70 m^2$
${1,05 m^3 \over 70 m^2} = 0,015 m = 15mm$
Det har regnet 15mm mens familien var borte.
Oppgave 4
a)
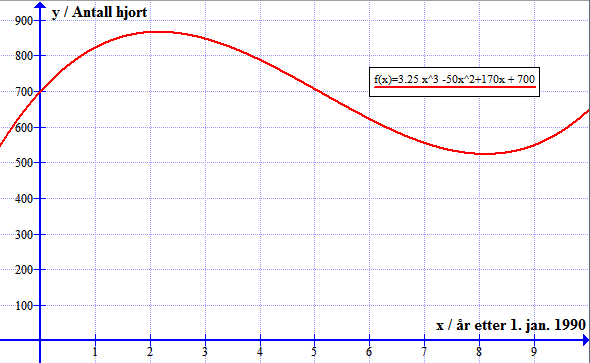
Bruker programmet Graph for å tegne grafen.
Framgangsmåte: Funksjon => sett inn funksjon
b)
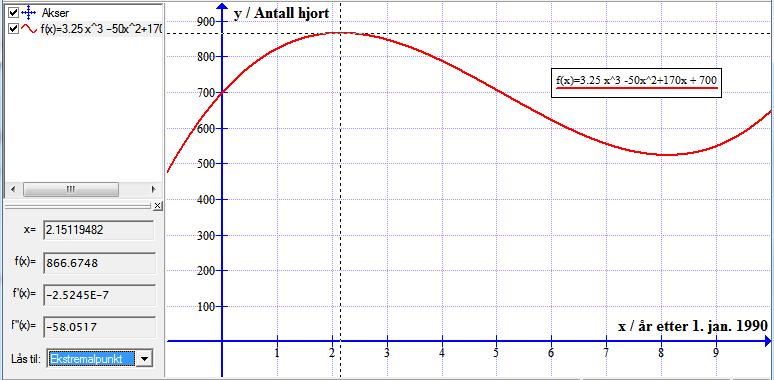
Framgangsmåte: Beregn => Beregn => Lås til ekstremalpunkt => klikk på grafen
Ser at grafen har et toppunkt i $t = 2.15$.
Hjortebestanden var størst i februar 1992. Da var bestanden på 867 dyr.
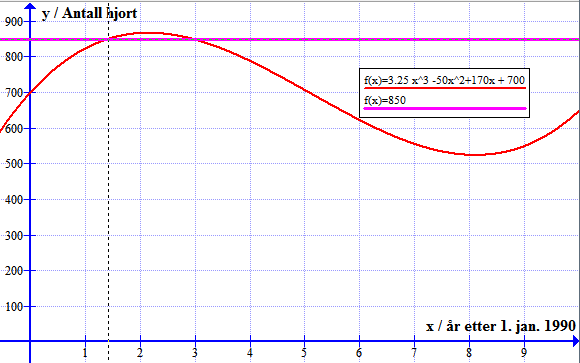
c) Framgangsmåte: Setter inn funksjonen f(t) = 850. Velger Beregn => Beregn => Lås til skjæringspunkt => klikker på grafen
Ser at vi har skjæringspunkt i $t=1,4$ og $t = 2,9$
Løsningen sier at hjortebestanden var på 850 dyr etter mai 1991 og november 1992.
d)
Leser ut av grafen at i $1994$ ($t =4$) er bestanden $788$ hjort. I $1998$ er bestanden $524$ hjort.
Antall år: $1998 - 1994 = 4 $
Endring i antall hjort: $524 - 788 = -264$
Endring per år: $\frac {-264}{4} = -66$
Bestanden av hjort minsker i gjennomsnitt med 66 dyr per år i perioden $1994$ til $1998$.
Oppgave 5
a)
Fordi alle terminbeløpene er like store, så er dette et annuitetslån.
b)
Legger sammen alle avdragene for å finne det totale lånebeløpet:
$6396 + 7010 + 7683 + 8420 +9229 + 10115 + 11086 + 12150 +13316 + 14595= 100000 kr$
Det totale lånebeløpet er 100000kr.
c)
Første termin (som er første år) betaler han renter på 100000 kr. Rentene er 9600kr.
${9600 \over 100000 } = 0,096 = 9,6 \%$
Renta er $9,6 \%$ per år.
Oppgave 6
a)
$V = \frac13 \pi r^2 h = \frac 13 \pi \cdot r^2 \cdot \frac 23 \cdot r= \frac13 \pi \cdot (1,35\,m)^2 \cdot 0,66 \cdot 1,35\,m \approx 1,72\,m^3$
b)
Løser likningen:
$ V = \frac13 \pi \cdot r^2 \cdot h \\ V= \frac 13 \pi \cdot \frac 94 h^2 \cdot h \\ h = \sqrt[3]{\frac{8,0\,m^3 \cdot 4}{3 \pi}} \\ \approx 1,5 m$
En kjegle med volum 8 kubikkmeter vil ha en høyde på ca 1,5 meter.