Løsning del 2 utrinn Høst 13: Forskjell mellom sideversjoner

Siste sideversjon per 24. jun. 2017 kl. 12:56

DEL 2

Oppgave 1

a)

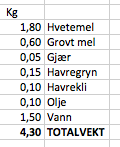
Ingredienser:

De veier 4,3 Kg, eller 4300 gram.

b)

Dersom vi deler alle mengden i oppskriften på 4, finner vi mengden for ett brød. Deretter ganger vi det med 5, siden vi skal lage fem brød. Det er det samme som å gange alle mengdene med $\frac{5}{4}$ :

Hvetemel: $\frac{5}{4} \cdot 1, 8 k g = 2, 25 k g$

Grovt mel: $\frac{5}{4} \cdot 600 g = 750 g$

Havregryn: $\frac{5}{4} \cdot 150 g = 188 g$

Havrekli: $\frac{5}{4} \cdot 100 g = 125 g$

Olje: $\frac{5}{4} \cdot 100 g = 125 g$

Vann $\frac{5}{4} \cdot 1, 5 l i t e r = 1, 88 l i t e r$

Oppgave 2

a)

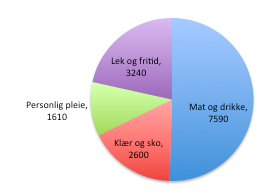
Oversikt over månedlige utgifter:

b)

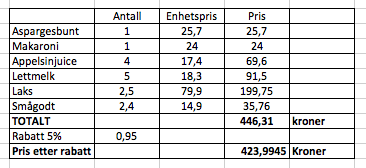
Hun må betale 424 kroner for varene.

Formelbruk:

c)

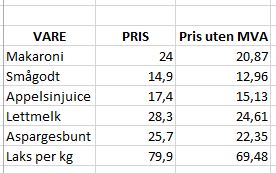
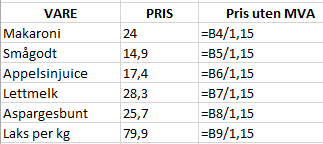
Merverdiavgiften er på 15%

Pris før MVA multiplisert med vekstfaktor er lik enhetspris, dvs:

$Pris uten MVA \cdot 1, 15 = E n h e t s p r i s Pris uten MVA = \frac{E n h e t s p r i s}{1, 15}$

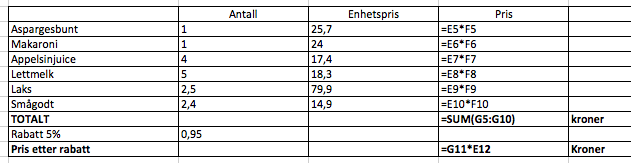
Legger man denne formelen inn i regnearket får man:

Oppgave 3

a)

40 liter tilsvarer $40 d m^{3}$ .

$1 m^{3} = 1000 d m^{3}$

For å få en kubikkmeter ved trenger man $\frac{1000}{40} = 25$ sekker.

Bjørkeved: $25 \cdot 75 k r = 1875$ kroner.

Granved: $25 \cdot 60 k r = 1500$ kroner.

b)

Energi per krone:

Bjørkeved: $\frac{2715 k W h}{1875 k r} = 1, 448$ kWh/ krone

Granved: $\frac{2150 k W h}{1500 k r} = 1, 433$ kwh/krone

På papiret gir bjørkeveden marginalt mere energi per krone, i praksis vil man neppe merke forskjell.

Oppgave 4

a)

Varmetap gjennom vindu:

$V = 10, 5 \cdot A \cdot T \cdot (I - U) V = 10, 5 \cdot (1, 1 m \cdot 0, 8 m) \cdot 24 \cdot (20 - 1) V = 4213, 44 k J$

b)

Det betyr at energien går utenfra og inn. Det skjer dersom U er større enn I.

Oppgave 5

a)

Hver av de fire sideflatene er to rettvinklede trekanter med hypotenus 17,0 cm. Det ene katetet er 5,0 cm, det andre h. Bruker pytagoras:

$h = \sqrt{17, 0^{2} - 5, 0^{2}} = 16, 2$ Høyden h i den likebeinte trekanten er 16,2 cm

Arealet av en trekant blir: $A = \frac{16, 2 c m \cdot 10, 0 c m}{2} = 81, 2 c m^{2}$

Pyramiden består av fire slike trekanter: Overflate av trekantene: $O = 4 \cdot 81, 2 c m^{2} = 325, 0 c m^{2}$

Vi må også ta med kvadratet i bunnen, den totale overflaten blir $425, 0 c m^{2}$

b)

For å finne H bruker vi pytagoras en gang til:

$H = \sqrt{16, 2^{2} - 5, 0^{2}} = 15, 4$

Høyden H i pyramiden er 15,4 centimeter.

Volum av pyramide (der G er grunnflaten):

$V = \frac{1}{3} \cdot G \cdot H = \frac{1}{3} \cdot 100, 0 c m^{2} \cdot 15, 4 c m = 513, 3 c m^{3}$

Volumet av pyramidekortet er $513, 3 c m^{3}$ .

c)

Her kan vi bruke formlikhet. Kaller halve lengden i det kvadratiske hullet for x:

$\frac{15, 4}{5, 4} = \frac{5}{x} x = 1, 75$

Sidekantene i det kvadratiske hullet må være 3,5 centimeter, for at "rammen" skal ligge 10 centimeter over grunnflaten.

Oppgave 6

a)

b)

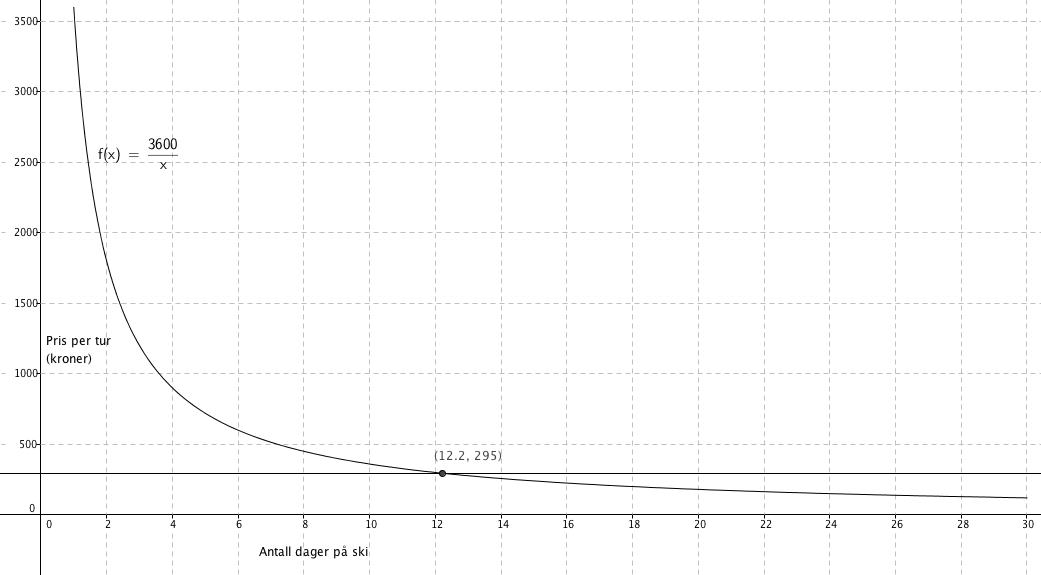
Skriver inn y = 295 og finner skjæringspunktet med grafen, for å se når pris per tur med sesongkort blir billigere enn dagskort. Ser at Kari må dra på ski mer enn 12 dager, altså 13 dager eller mer for at det skal lønne seg med sesongkort.

Oppgave 7

a)

Kombinasjoner som gir syv øyner på to terninger er (1,6), (2,5), (3,4), (4,3), (5,2) og (6,1), altså seks utfall.

P(sum øyne syv)= $\frac{6}{36} = \frac{1}{6}$

b)

Mulige primtall er 2, 3, 5, 7 og 11.

Tilsvarende opptelling som i a gir 15 gunstige utfall.

P(primtall)= $\frac{15}{36} = \frac{5}{12}$

Oppgave 8

a)

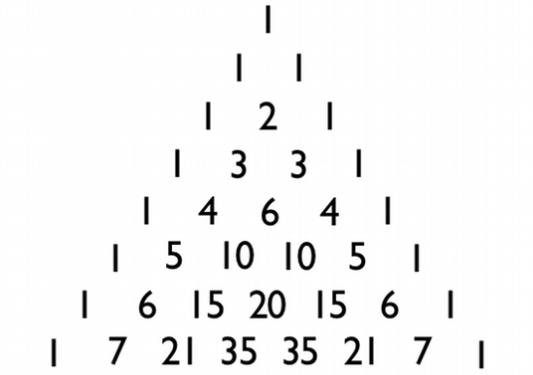
Sum: $1 1 + 1 = 2 1 + 2 + 1 = 4 1 + 3 + 3 + 1 = 8 1 + 4 + 6 + 4 + 1 = 16 1 + 5 + 10 + 10 + 5 + 1 = 32 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 1 + 7 + 21 + 35 + 35 + 21 + 7 + 1 = 128$

Som potenser med grunntall 2:

$2,^{0}, 2^{1}, 2^{2}, 2^{3}, 2^{4}, 2^{5}, 2^{6} o g 2^{7}$

b)

$[\begin{matrix} 21 + x = y \\ 2 x + y = 126 \end{matrix}]$

Legger sammen likningene og får:

$21 + x + 2 x + y = 126 + y 3 x = 105 x = 35$

Innsatt gir det x = 35 og y = 56.

Oppgave 9

a)

$V_{1} + V_{2} + V_{3} + V_{4} + V_{5} + V_{6} + V_{7} + V_{8} = a^{2} b + a^{3} + a b^{2} + a^{2} b + a b^{2} + b^{3} + a^{2} b + a b^{2} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$

b)

$(a + b)^{0} = 1 (a + b)^{1} = a + b (a + b)^{2} = a^{2} + 2 a b + b^{2} (a + b)^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$

Koeffisienten foran variablene a og b er dem man finner på radene i Pascals talltrekant.

@@ Linje 53: / Linje 53: @@
 Pris før MVA multiplisert med vekstfaktor er lik enhetspris, dvs:
-$PrisutenMVA \cdot 1,15 = Enhetspris \ PrisutenMVA = \frac{Enhetspris}{1,15}$
+$\text{Pris uten MVA} \cdot 1,15 = Enhetspris \ \text{Pris uten MVA} = \frac{Enhetspris}{1,15}$
 Legger man denne formelen  inn i regnearket får man:
@@ Linje 108: / Linje 108: @@
 Arealet av en trekant blir:  $A = \frac{16, 2 c m \cdot 10, 0 c m}{2} = 81, 2 c m^{2}$
-Pyramiden består av fire slike trekanter: Overflate:  $O = 4 \cdot 81, 2 c m^{2} = 325, 0 c m^{2}$
+Pyramiden består av fire slike trekanter: Overflate av trekantene:  $O = 4 \cdot 81, 2 c m^{2} = 325, 0 c m^{2}$
-Om vi også tar med kvadratet i bunnen blir den totale overflaten  $425, 0 c m^{2}$
+Vi må også ta med kvadratet i bunnen, den totale overflaten blir  $425, 0 c m^{2}$
 ===b)===
@@ Linje 120: / Linje 120: @@
 Høyden H i pyramiden er 15,4 centimeter.
-Volum av pyramide:
+Volum av pyramide (der G er grunnflaten):
-$V= \frac {1}{3}\cdot A \cdot H = \frac 13 \cdot 100,0 cm^2 \cdot 15,4cm = 513,6 cm^3$
+$V= \frac {1}{3}\cdot G \cdot H = \frac 13 \cdot 100,0 cm^2 \cdot 15,4cm = 513,3 cm^3$
-Volumet av pyramidekortet er $513,6 cm^3$.
+Volumet av pyramidekortet er $513,3 cm^3$.
 ===c)===
@@ Linje 142: / Linje 142: @@
 ===b)===
-Man ser fra figuren i a, at dersom Kari er på ski 14 dager eller mere vil det lønne seg med sesongkort.
+Skriver inn y = 295 og finner skjæringspunktet med grafen, for å se når pris per tur med sesongkort blir billigere enn dagskort. Ser at Kari må dra på ski mer enn 12 dager, altså 13 dager eller mer for at det skal lønne seg med sesongkort.
 ==Oppgave 7==
@@ Linje 154: / Linje 154: @@
 ===b)===
-Mulige primtall er 3, 5, 7 og 11.
+Mulige primtall er 2, 3, 5, 7 og 11.
-Tilsvarende opptelling som i a gir 14 gunstige utfall.
+Tilsvarende opptelling som i a gir 15 gunstige utfall.
-P(primtall)=$ \frac{14}{36}= \frac {7}{18}$
+P(primtall)=$ \frac{15}{36}= \frac {5}{12}$
 ==Oppgave 8==
@@ Linje 167: / Linje 167: @@
 Sum:
-$1 \ 1+1=2\1+2+1=3 \ 1+3+3+1 = 8 \ 1+4+6+4+1 = 16 \ 1+5+10+10+5+1 = 32 \ 1+6+15+20+15+6+1 = 64 \ 1+7+21+35+35+21+7+1= 128 $
+$1 \ 1+1=2\1+2+1=4 \ 1+3+3+1 = 8 \ 1+4+6+4+1 = 16 \ 1+5+10+10+5+1 = 32 \ 1+6+15+20+15+6+1 = 64 \ 1+7+21+35+35+21+7+1= 128 $