Løsning del 1 utrinn Vår 17: Forskjell mellom sideversjoner
| (56 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 20: | Linje 20: | ||
Vi multipliserer 0,5 kg med 12 og får 6,0 kg. | Vi multipliserer 0,5 kg med 12 og får 6,0 kg. | ||
12 kurver veier 6 kilogram. | |||
===b)=== | ===b)=== | ||
| Linje 30: | Linje 32: | ||
==Oppgave 3== | ==Oppgave 3== | ||
$(-2)^2 \cdot 2^0 = 4 \cdot 1=4 \\ -2^2 \cdot 2^1 = -4 \cdot 2 = -8 \\ -(2-2^2)= -(2-4)=2 \\ \frac{2 \cdot (-2)}{2+2} = -1$ | |||
Vi ser at uttrykk nr to fra venstre har den laveste verdien. | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | ===a)=== | ||
$\frac{1}{6} + \frac{1}{3} = \frac{1}{6} + \frac{2}{6} = \frac{1+2}{6} = \frac 12$ | |||
===b)=== | ===b)=== | ||
$\frac{0,2 \cdot 0,4}{0,16} = \frac {2 \cdot 4}{16} = \frac 12$ | |||
Ganget med 100 i teller og nevner, så slipper man unna desimaltallene. | |||
==Oppgave 5== | ==Oppgave 5== | ||
Når et punkt A skal speiles om en linje skal avstanden fra punktet til linjen være like langt som fra linjen til "speilpunktet", A'. | |||
Figur fire oppfyller dette kravet. | |||
==Oppgave 6== | ==Oppgave 6== | ||
Vi har da to gunnstige ( 3 eller 5), av seks mulige. Sannsynligheten blir da: P( 3 eller 5) = $\frac 26 = \frac 13$ | |||
==Oppgave 7== | ==Oppgave 7== | ||
Sannsynligheten for mynt (eller kron) er 50% = $ \frac 12$ på ett kast. Kaster vi tre mynter får vi: | |||
P(mynt, mynt, mynt) = P(kron, kron, kron) = $ \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac 18$ | |||
Det er en åttenedels sjanse for tre "kron", eller tre "mynt", derfor adderer vi brøkene. | |||
1/8 + 1/8 = 2/8 = 1/4 | |||
==Oppgave 8== | ==Oppgave 8== | ||
Overslag: vi runder den ene faktoren opp, og den andre ned: | |||
$88,95 \approx 90$ og $10,21 \approx 10$ og får $90 \cdot 10 = 900$, prisen var ca. 900 kroner. | |||
==Oppgave 9== | ==Oppgave 9== | ||
Kombinatorikk - fakultet: | |||
Første person kan velge mellom 8 stoler. Neste person kan velge mellom 7, osv. De kan altså sette seg på $8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 8$! måter. | |||
==Oppgave 10== | ==Oppgave 10== | ||
Formelomforming: | |||
$A= \frac{gh}{2} \\ 2A = gh \\h= \frac{2A}{g}$ | |||
==Oppgave 11== | ==Oppgave 11== | ||
===a)=== | |||
$\frac{a+a+a}{a} = \frac{3a}{a}=3$ | |||
===b)=== | |||
$\frac{a^2-b^2}{a-b} = \frac{(a+b)(a-b)}{a-b} = a+b $ | |||
==Oppgave 12== | ==Oppgave 12== | ||
===a)=== | |||
$4x-4= 11 -x \\4x+ x = 11 + 4 \\ 5x=15 \\ x=3$ | |||
===b)=== | |||
$ \frac{x}{6} - \frac{2-x}{4} =2 \quad | \cdot 12 \\ 2x - 3(2-x) =24 \\ 2x - 6+3x = 24 \\ 5x=30 \\ x=6$ | |||
==Oppgave 13== | ==Oppgave 13== | ||
Avstanden til månen er 384 000 000 m = $3,84 \cdot 10^8 m$. | |||
==Oppgave 14== | ==Oppgave 14== | ||
Dette kan gjøres på flere måter, | |||
Metode 1 | |||
$ 1 : 15 \: 000 \\ 3 : 45\: 000 \\ 45 \: 000 \text{cm} = 450 \text{m}$ | |||
I virkeligheten er avstanden 450 m. | |||
Metode 2 | |||
$ \frac 3x = \frac{1}{15\: 000} \\x= 45\:000$ | |||
I virkeliheten er avstanden 45 000 cm eller 450 meter, eller 0,45 km. | |||
==Oppgave 15== | ==Oppgave 15== | ||
===a)=== | |||
Starter i origo, en bort og to opp: A ( 1, 2) | |||
===b)=== | |||
y = ax + b, a er stigningstallet og b er skjæring med y-aksen. | |||
Grafen skjærer y-aksen i 4 og synker to når man går en til høyre: | |||
y=-2x + 4 | |||
==Opphave 16== | ==Opphave 16== | ||
Kan løses som to likninger med to ukjente, | |||
Kall pandaen for $x$ og tigergutt for $y$ | |||
$\begin{bmatrix} \text{I} \:\: 2x + y = 350 \\ \text{II} \:\: 2x + 2y = 500 \end{bmatrix} \\$ | |||
$\text{I}\\ y = 350 - 2x$ | |||
Setter likning I inn i II | |||
$\text{II} \\ 2x + 2 ( 350 - 2x) = 500 \\ 2x + 700 - 4x = 500 \\ -2x = -200 \quad | : (-2) \\ x = 100$ | |||
Fra likning I får vi $ y = 350 - 2 (100) = 150$ | |||
En panda koster 100 kr og tigergutt koster 150 kr. | |||
Alternativt kan det løses slik | |||
Forskjellen mellom linje en og to er en tigergutt og 150 kroner. En tigergutt koster derfor 150 kroner. Da må en panda koste 100 kroner. | |||
===a)=== | ===a)=== | ||
En panda koster 100 kroner. | |||
===b)=== | ===b)=== | ||
En tigergutt koster 150 kroner. | |||
==Oppgave 17== | ==Oppgave 17== | ||
Skoene kostet nesten 1000 kroner. 20% av 1000 er 200. De ble satt ned med nesten 200 kroner. | |||
==Oppgave 18== | ==Oppgave 18== | ||
AB er hypotenusen: | |||
AB = $\sqrt{6^2 +8^2} = \sqrt{36 + 64} = \sqrt{100}= 10$ cm | |||
==Oppgave 19== | ==Oppgave 19== | ||
$\frac 15 = \frac{2}{10}$. Altså 2 dL saft og 10 dL vann, dvs. mugge nr. fire. | |||
==Oppgave 20== | ==Oppgave 20== | ||
===a)=== | ===a)=== | ||
13/39 = 1/3 | |||
En tredjedel sykklet eller gikk til skolen. | |||
===b)=== | ===b)=== | ||
12 er litt mindre enn1/3 av 39, altså ca. 30%. | |||
==Oppgave 21== | ==Oppgave 21== | ||
BC i den lille trekanten tilsvarer EF i den store og AB tilsvarer DE. | |||
Løst som likning: | |||
$\frac{AB}{DE} = \frac{BC}{EF} \\ \frac{AB}{12} = \frac 6 9 \\ AB = 8$ | |||
Lengden av AB er 8. | |||
==Oppgave 22== | ==Oppgave 22== | ||
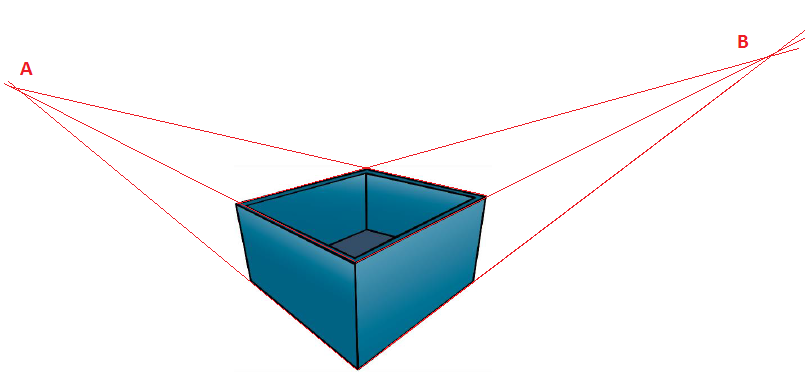
[[File:kasse.png]] | |||
Forsvinningspunkter i A og B. | |||
==Oppgave 23== | ==Oppgave 23== | ||
Siden høyden er den samme på begge vil grunnflaten avgjøre volumet. Prismet har en grunnflate på $27cm^2$ Grunnflaten til sylinderen er den samme dersom vi setter $\pi$ lik tre. Siden $\pi$ er større enn tre blir grunnflaten av sylinderen større enn grunnflaten til prismet, dermed også volumet av sylinderen størst. | |||
Sylinderen har et større volum enn prismet. | |||
==Oppgave 24== | ==Oppgave 24== | ||
Høyde h = 5: | |||
Overflate prisme: | |||
$2 \cdot 3,0 cm \cdot 9,0 cm + 2 \cdot 3,0cm \cdot 5,0 cm + 2 \cdot 9,0 cm \cdot 5,0 cm = 54,0 cm^2 + 30,0cm^2 + 90,0cm^2 = 174,0 cm^2 $ | |||
Overflate sylinder: | |||
$2 \cdot \pi \cdot (3,0cm)^2 + 2 \cdot \pi \cdot 3,0 cm \cdot 5,0cm = 18,0 \pi cm^2 + 30,0 \pi cm^2 = 48 \pi cm^2 \approx 150,72 cm^2$ | |||
==Oppgave 25== | ==Oppgave 25== | ||
===a)=== | ===a)=== | ||
Vi ser at når figurnummerert øker med en så øker antall fyrstikker med to. I figur nr 3 er det 7 fyrstikker, i figur 4 er det 9, og, i figur 5 er det 11 fyrstikker. | |||
===b)=== | ===b)=== | ||
Vi setter figurnummer lik n. | |||
Figur 1 har en mer enn det dobbelte av figurnummeret: 1 pluss 2 ganger 1. | |||
Figur 2: $1+ 2 \cdot 2$ | |||
Figur 5: $1 +2 \cdot 5$ | |||
Figur n: 2n+1. | |||
Siste sideversjon per 12. mai 2018 kl. 08:10
Løsningsforslag for del 1 og del 2 fra matteprat
Del 1
Oppgave1
a)
$657 + 468 = 1125$
b)
$52 \cdot 48= 2496$
Oppgave 2
a)
500 g = 0,5 kg
Vi multipliserer 0,5 kg med 12 og får 6,0 kg.
12 kurver veier 6 kilogram.
b)
12 L = 12 liter = 120 desiliter = 120dL
$120 :4= 30$
Man trenger 30 flasker.
Oppgave 3
$(-2)^2 \cdot 2^0 = 4 \cdot 1=4 \\ -2^2 \cdot 2^1 = -4 \cdot 2 = -8 \\ -(2-2^2)= -(2-4)=2 \\ \frac{2 \cdot (-2)}{2+2} = -1$
Vi ser at uttrykk nr to fra venstre har den laveste verdien.
Oppgave 4
a)
$\frac{1}{6} + \frac{1}{3} = \frac{1}{6} + \frac{2}{6} = \frac{1+2}{6} = \frac 12$
b)
$\frac{0,2 \cdot 0,4}{0,16} = \frac {2 \cdot 4}{16} = \frac 12$
Ganget med 100 i teller og nevner, så slipper man unna desimaltallene.
Oppgave 5
Når et punkt A skal speiles om en linje skal avstanden fra punktet til linjen være like langt som fra linjen til "speilpunktet", A'.
Figur fire oppfyller dette kravet.
Oppgave 6
Vi har da to gunnstige ( 3 eller 5), av seks mulige. Sannsynligheten blir da: P( 3 eller 5) = $\frac 26 = \frac 13$
Oppgave 7
Sannsynligheten for mynt (eller kron) er 50% = $ \frac 12$ på ett kast. Kaster vi tre mynter får vi:
P(mynt, mynt, mynt) = P(kron, kron, kron) = $ \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac 18$
Det er en åttenedels sjanse for tre "kron", eller tre "mynt", derfor adderer vi brøkene.
1/8 + 1/8 = 2/8 = 1/4
Oppgave 8
Overslag: vi runder den ene faktoren opp, og den andre ned:
$88,95 \approx 90$ og $10,21 \approx 10$ og får $90 \cdot 10 = 900$, prisen var ca. 900 kroner.
Oppgave 9
Kombinatorikk - fakultet:
Første person kan velge mellom 8 stoler. Neste person kan velge mellom 7, osv. De kan altså sette seg på $8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 8$! måter.
Oppgave 10
Formelomforming:
$A= \frac{gh}{2} \\ 2A = gh \\h= \frac{2A}{g}$
Oppgave 11
a)
$\frac{a+a+a}{a} = \frac{3a}{a}=3$
b)
$\frac{a^2-b^2}{a-b} = \frac{(a+b)(a-b)}{a-b} = a+b $
Oppgave 12
a)
$4x-4= 11 -x \\4x+ x = 11 + 4 \\ 5x=15 \\ x=3$
b)
$ \frac{x}{6} - \frac{2-x}{4} =2 \quad | \cdot 12 \\ 2x - 3(2-x) =24 \\ 2x - 6+3x = 24 \\ 5x=30 \\ x=6$
Oppgave 13
Avstanden til månen er 384 000 000 m = $3,84 \cdot 10^8 m$.
Oppgave 14
Dette kan gjøres på flere måter,
Metode 1
$ 1 : 15 \: 000 \\ 3 : 45\: 000 \\ 45 \: 000 \text{cm} = 450 \text{m}$
I virkeligheten er avstanden 450 m.
Metode 2
$ \frac 3x = \frac{1}{15\: 000} \\x= 45\:000$
I virkeliheten er avstanden 45 000 cm eller 450 meter, eller 0,45 km.
Oppgave 15
a)
Starter i origo, en bort og to opp: A ( 1, 2)
b)
y = ax + b, a er stigningstallet og b er skjæring med y-aksen.
Grafen skjærer y-aksen i 4 og synker to når man går en til høyre:
y=-2x + 4
Opphave 16
Kan løses som to likninger med to ukjente,
Kall pandaen for $x$ og tigergutt for $y$
$\begin{bmatrix} \text{I} \:\: 2x + y = 350 \\ \text{II} \:\: 2x + 2y = 500 \end{bmatrix} \\$
$\text{I}\\ y = 350 - 2x$
Setter likning I inn i II
$\text{II} \\ 2x + 2 ( 350 - 2x) = 500 \\ 2x + 700 - 4x = 500 \\ -2x = -200 \quad | : (-2) \\ x = 100$
Fra likning I får vi $ y = 350 - 2 (100) = 150$
En panda koster 100 kr og tigergutt koster 150 kr.
Alternativt kan det løses slik
Forskjellen mellom linje en og to er en tigergutt og 150 kroner. En tigergutt koster derfor 150 kroner. Da må en panda koste 100 kroner.
a)
En panda koster 100 kroner.
b)
En tigergutt koster 150 kroner.
Oppgave 17
Skoene kostet nesten 1000 kroner. 20% av 1000 er 200. De ble satt ned med nesten 200 kroner.
Oppgave 18
AB er hypotenusen:
AB = $\sqrt{6^2 +8^2} = \sqrt{36 + 64} = \sqrt{100}= 10$ cm
Oppgave 19
$\frac 15 = \frac{2}{10}$. Altså 2 dL saft og 10 dL vann, dvs. mugge nr. fire.
Oppgave 20
a)
13/39 = 1/3
En tredjedel sykklet eller gikk til skolen.
b)
12 er litt mindre enn1/3 av 39, altså ca. 30%.
Oppgave 21
BC i den lille trekanten tilsvarer EF i den store og AB tilsvarer DE.
Løst som likning:
$\frac{AB}{DE} = \frac{BC}{EF} \\ \frac{AB}{12} = \frac 6 9 \\ AB = 8$
Lengden av AB er 8.
Oppgave 22
Forsvinningspunkter i A og B.
Oppgave 23
Siden høyden er den samme på begge vil grunnflaten avgjøre volumet. Prismet har en grunnflate på $27cm^2$ Grunnflaten til sylinderen er den samme dersom vi setter $\pi$ lik tre. Siden $\pi$ er større enn tre blir grunnflaten av sylinderen større enn grunnflaten til prismet, dermed også volumet av sylinderen størst.
Sylinderen har et større volum enn prismet.
Oppgave 24
Høyde h = 5:
Overflate prisme:
$2 \cdot 3,0 cm \cdot 9,0 cm + 2 \cdot 3,0cm \cdot 5,0 cm + 2 \cdot 9,0 cm \cdot 5,0 cm = 54,0 cm^2 + 30,0cm^2 + 90,0cm^2 = 174,0 cm^2 $
Overflate sylinder:
$2 \cdot \pi \cdot (3,0cm)^2 + 2 \cdot \pi \cdot 3,0 cm \cdot 5,0cm = 18,0 \pi cm^2 + 30,0 \pi cm^2 = 48 \pi cm^2 \approx 150,72 cm^2$
Oppgave 25
a)
Vi ser at når figurnummerert øker med en så øker antall fyrstikker med to. I figur nr 3 er det 7 fyrstikker, i figur 4 er det 9, og, i figur 5 er det 11 fyrstikker.
b)
Vi setter figurnummer lik n.
Figur 1 har en mer enn det dobbelte av figurnummeret: 1 pluss 2 ganger 1.
Figur 2: $1+ 2 \cdot 2$
Figur 5: $1 +2 \cdot 5$
Figur n: 2n+1.