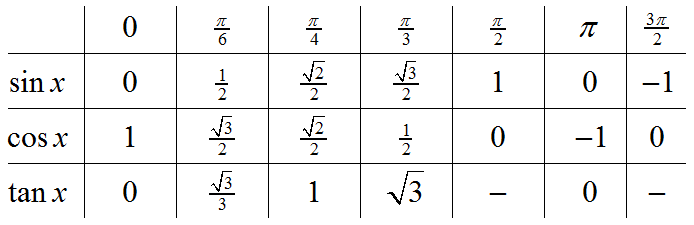Trigonometri R2: Forskjell mellom sideversjoner
m Endret beskyttelsesnivå for «Trigonometri R2» ([move=sysop] (ubestemt)) |
|||
| (86 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 5: | Linje 5: | ||
[[Bilde:Trigrad.png]] | [[Bilde:Trigrad.png]] | ||
Vi konstruerer en sirkelbue med lengde < | Vi konstruerer en sirkelbue med lengde <math>s</math> og radius <math>r</math>, som vist på figuren. Buen er avgrenset av de to radiene som går fra sentrum av buen. Vinkelen mellom de to radiene i radianer er da definert som | ||
$$\alpha=\frac{s}{r}$$ | |||
Det følger at forholdet mellom radianer og grader er gitt ved | Det følger at forholdet mellom radianer og grader er gitt ved | ||
:< | :<math>360^\circ=2\pi</math> | ||
eller ekvivalent ved | eller ekvivalent ved | ||
:< | :<math>v[^\circ]=\frac{180^\circ}{\pi}v[\text{rad}]</math> for en vinkel <math>v</math> | ||
==Trigonometeriske funksjoner== | ==Trigonometeriske funksjoner== | ||
De tre sentrale trigonometriske funksjonene er sinus, cosinus og tangens, som er et produkt av sinus og cosinus. Sinus er den viktigste trigonometriske funksjonen, siden alle de andre trigonometriske funksjonene kan utledes fra denne. | De tre sentrale trigonometriske funksjonene er sinus, cosinus og tangens, som er et produkt av sinus og cosinus. Sinus er den viktigste trigonometriske funksjonen, siden alle de andre trigonometriske funksjonene kan utledes fra denne. | ||
==Enhetssirkelen== | |||
Enhetssirkelen har sentrum i origo og radius en. | |||
===Definisjon av sin x og cos x=== | ===Definisjon av sin x og cos x=== | ||
| Linje 27: | Linje 31: | ||
[[Bilde:Trig1.png]] | [[Bilde:Trig1.png]] | ||
Når vi konstruerer en enhetssirkel og en radius med vinkel < | Når vi konstruerer en enhetssirkel og en radius med vinkel <math>\alpha</math> på x-aksen slik figuren viser, vil radien skjære sirkelperiferien i punktet <math>P</math>. Hvis trekker normalene fra <math>P</math> på koordinataksene, vil de skjære disse i punktene <math>A</math> og <math>B</math> slik figuren viser. Da vil y-verdien til punktet <math>A</math> være lik <math>\sin\,\alpha</math> og x-verdien til punktet <math>B</math> være lik <math>\cos\,\alpha</math> | ||
Når vi plotter sinus- og cosinuskurvene ser de slik ut: | Når vi plotter sinus- og cosinuskurvene ser de slik ut: | ||
| Linje 33: | Linje 37: | ||
[[Bilde:Trig2.png]] | [[Bilde:Trig2.png]] | ||
Sinus- og cosinuskurvene har begge perioder på < | Sinus- og cosinuskurvene har begge perioder på <math>2\pi</math> radianer. | ||
Merk at cosinusfunksjonen kun er sinusfunkjsonen forskjøvet < | Merk at cosinusfunksjonen kun er sinusfunkjsonen forskjøvet <math>\frac{\pi}{2}</math> radianer i minusretningen. Altså gjelder det at <math>sin(x+\frac{\pi}{2})=\cos\,x</math> | ||
===Definisjon av tan(x)=== | ===Definisjon av tan(x)=== | ||
| Linje 41: | Linje 45: | ||
Tangensfunksjonen er definert slik at | Tangensfunksjonen er definert slik at | ||
:< | :<math>\tan\,x=\frac{\sin\,x}{\cos\,x}</math> | ||
Når vi plotter tangenskurven, ser den slik ut: | Når vi plotter tangenskurven, ser den slik ut: | ||
| Linje 47: | Linje 51: | ||
[[Bilde:Trigtan.png]] | [[Bilde:Trigtan.png]] | ||
Tangenskurven har en periode på < | Tangenskurven har en periode på <math>\pi</math> radianer. | ||
===Fortegn av trigonometriske funksjoner=== | ===Fortegn av trigonometriske funksjoner=== | ||
| Linje 53: | Linje 57: | ||
[[Bilde:Trigfortegn.png]] | [[Bilde:Trigfortegn.png]] | ||
Dette diagrammet viser fortegnene til de forskjellige trigonometriske funksjonene for forskjellige vinkler. Den sorte streken gjennom tangensdiagrammet viser vinklene der < | Dette diagrammet viser fortegnene til de forskjellige trigonometriske funksjonene for forskjellige vinkler. Den sorte streken gjennom tangensdiagrammet viser vinklene der <math>\tan\,x</math> går mot <math>\pm\infty</math>. Vi får et bruddpunkt, og det er derfor meningsløst å snakke of fortegnet til <math>\tan\,x</math> når <math>x=\frac{\pi}{2}</math> eller <math>x=\frac{3\pi}{2}</math>. | ||
Hvis du kan disse diagrammene utanat, vil du kunne vurdere hvilke løsninger du forventer til trigonometriske ligninger. Det vil bli lettere å vurdere om løsningene stemmer. | Hvis du kan disse diagrammene utanat, vil du kunne vurdere hvilke løsninger du forventer til trigonometriske ligninger. Det vil bli lettere å vurdere om løsningene stemmer. | ||
===Noen viktige verdier av sin x, cos x og tan x=== | ===Noen viktige verdier av sin x, cos x og tan x på tabellform=== | ||
Verdiene i tabellen under bør du memorisere. Å kunne disse utenat vil være til stor hjelp i løsingen av trigonometriske ligninger. | Verdiene i tabellen under bør du memorisere. Å kunne disse utenat vil være til stor hjelp i løsingen av trigonometriske ligninger. | ||
[[Bilde:Trigverdier.png]] | [[Bilde:Trigverdier.png]] | ||
===Noen viktige verdier av sin x, cos x og tan x i enhetssirkelen (1. kvadrant)=== | |||
[[Bilde:forste-kvadrant-1.png]] | |||
===Viktige trigonometriske identiteter=== | ===Viktige trigonometriske identiteter=== | ||
| Linje 67: | Linje 77: | ||
Ettersom alle de trigonometriske funksjonene er periodiske, vil de samme verdiene gå igjen for hver syklus. Generellt gjelder det at | Ettersom alle de trigonometriske funksjonene er periodiske, vil de samme verdiene gå igjen for hver syklus. Generellt gjelder det at | ||
:< | :<math>\sin(x+2\pi)=\sin\,x</math> | ||
:< | :<math>\cos(x+2\pi)=\cos\,x</math> | ||
:< | :<math>\tan(x+\pi)=\tan\,x</math> | ||
Å være klar over disse sammenhengene vil ha betydning når vi senere vurderer løsninger av trigonometriske ligninger. | Å være klar over disse sammenhengene vil ha betydning når vi senere vurderer løsninger av trigonometriske ligninger. | ||
| Linje 77: | Linje 87: | ||
Ut ifra figuren om [[Trigonometri#Definisjon_av_sin_x_og_cos_x|definisjonen av sinus og cosinus]] kan vi se flere egenskaper ved funksjonene. Spesifikt, | Ut ifra figuren om [[Trigonometri#Definisjon_av_sin_x_og_cos_x|definisjonen av sinus og cosinus]] kan vi se flere egenskaper ved funksjonene. Spesifikt, | ||
:< | :<math>\sin(\pi-x)=\sin\,x</math> | ||
:< | :<math>\sin(-x)=-\sin\,x</math> | ||
:< | :<math>\cos(2\pi-x)=\cos\,x</math> | ||
:< | :<math>\tan(-x)=-\tan\,x</math> | ||
De trigonometriske funksjonene har mange viktige relasjoner med hverandre. Noe som gjelder per definisjon for sinus og cosinus er identiteten | De trigonometriske funksjonene har mange viktige relasjoner med hverandre. Noe som gjelder per definisjon for sinus og cosinus er identiteten | ||
:< | :<math>\sin^2x+\cos^2x=1</math> | ||
som lett kan vises geometrisk med [[Trekanter#Rettvinklet_Trekant|Pythagorassetningen]], se figuren om [[Trigonometri#Definisjon_av_sin_x_og_cos_x|definisjonen av sinus og cosinus]].Denne identiteten er viktig fordi den lar oss omforme sinus til cosinus og omvendt. | som lett kan vises geometrisk med [[Trekanter#Rettvinklet_Trekant|Pythagorassetningen]], se figuren om [[Trigonometri#Definisjon_av_sin_x_og_cos_x|definisjonen av sinus og cosinus]].Denne identiteten er viktig fordi den lar oss omforme sinus til cosinus og omvendt. | ||
| Linje 93: | Linje 103: | ||
Som vi senere skal se, henger også tangens sammen med cosinus på følgende måte: | Som vi senere skal se, henger også tangens sammen med cosinus på følgende måte: | ||
:< | :<math>\tan^2x+1=\frac{1}{\cos^2x}</math> | ||
Denne identiteten beviser vi lenger nede i artikkelen. | Denne identiteten beviser vi lenger nede i artikkelen. | ||
| Linje 99: | Linje 109: | ||
===Inverse trigonometriske funksjoner=== | ===Inverse trigonometriske funksjoner=== | ||
Vi definerer de inverse trigonometriske funksjonene < | Vi definerer de inverse trigonometriske funksjonene <math>\arcsin</math>, <math>\arccos</math> og <math>\arctan</math> slik at | ||
:< | :<math>\arcsin(\sin\,x)=x\,,\,x\in [-\frac{\pi}{2},\frac{\pi}{2}]</math> | ||
:< | :<math>\arccos(\cos\,x)=x\,,\,x\in [0,\pi]</math> | ||
:< | :<math>\arctan(\tan\,x)=x\,,\,x\in <-\frac{\pi}{2},\frac{\pi}{2} ></math> | ||
Dersom < | Dersom <math>x</math> ikke befinner seg i disse mengdene, vil du likevel få en verdi innenfor disse mengdene. Ha dette i bakhodet når du løser trigonometriske ligninger på kalkulator. | ||
<p></p> | |||
I mange lærebøker i den videregående skole, og på kalkulatoren er notasjonen slik:<p></p> | |||
<math>arcsinx = sin^{-1}x\,,\ arccos x = cos^{-1} x \,,\ arctan x = tan^{-1} x</math> | |||
==Sumformelen for sin x og cos x== | ==Sumformelen for sin x og cos x== | ||
| Linje 113: | Linje 126: | ||
Hvis vi vet verdien av sinus og cosinus til to forskjellige vinkler, kan vi finne sinus og cosinus til summen av vinklene. Vi vet at | Hvis vi vet verdien av sinus og cosinus til to forskjellige vinkler, kan vi finne sinus og cosinus til summen av vinklene. Vi vet at | ||
:< | :<math>\sin(v\pm u)=\sin\,v\,\cos\,u\pm\cos\,v\,\sin\,u</math> | ||
og | og | ||
:< | :<math>\cos(v\pm u)=\cos\,v\,\cos\,u\mp \sin\,v\,\sin\,u</math> | ||
Også disse identitetene kan bevises geometrisk. | Også disse identitetene kan bevises geometrisk. | ||
Spesialtilfellet <math>u=v</math> er verdt å merke seg, siden disse av og til dukker opp i ligninger: | |||
:<math>\sin(2v)=2\sin\,v\,\cos\,v</math> | |||
:<math>\cos(2v)=\cos^2v-\sin^2v</math> | |||
==Trigonometriske ligninger== | ==Trigonometriske ligninger== | ||
| Linje 125: | Linje 144: | ||
Trigonometriske ligninger er ligninger der trigonometriske funksjoner av variabler inngår. Disse er nyttige i mange abstrakte og fysiske situasjoner. | Trigonometriske ligninger er ligninger der trigonometriske funksjoner av variabler inngår. Disse er nyttige i mange abstrakte og fysiske situasjoner. | ||
I denne seksjonen presenteres løsningsmetoder for de forskjellige typene trigonometriske ligninger. | |||
===Løsninger og definisjonsmengde=== | |||
I mange trigonometriske ligninger er definisjonsmengden til variabelen gitt på forhånd. Definisjonsmengden har innflytelse ikke bare på hva løsningene er, men også hvor mange løsninger som finnes. Dersom det ikke er gitt noen definisjonsmengde kan variabelen ha enhver reell verdi. For å få med alle løsninger bruker vi et lite triks, som vi viser nedenfor. | |||
Når definisjonsmengden er gitt, bør du først se om du kan forhåndsbestemme hvor mange løsninger du forventer å få. Gitt at ligningen er løselig er det akseptabelt å forvente to løsninger per <math>2\pi</math>-syklus av de trigonometriske funksjonene. Her er et eksempel: | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
:'''Eksempel''' | |||
:[[Bilde:TrigLign1.png]] | |||
:Bildet viser en plott av funksjonen <math>f(x)=3\sin(2x)+2\cos(2x)+1</math>. Nullpunktene til funksjonen, markert med grå prikker, viser løsningene til ligningen <math>3\sin(2x)+2\cos(2x)=-1</math>. Hvis definisjonsmengden er <math>x\in [0,\pi></math>, går funksjonene gjennom én <math>2\pi</math>-syklus, og vi får 2 løsninger. Hvis definisjonsmengden er <math>x\in [0,2\pi></math>, går funksjonene gjennom to <math>2\pi</math>-sykluser, og nå får vi 4 løsninger. | |||
:'''OBS!''' | |||
:Regelen om 2 løsninger per syklus gjelder bare hvis vi kan uttrykke ligningen ved én enkelt trigonometrisk funksjon, og denne ikke har sin største eller minste verdi. Som vi skal se senere kan funksjonen over beskrives på formen <math>f(x)=A\sin(x+\phi)+d</math>. | |||
</div> | |||
==Derivasjon av trigonometriske funksjoner== | ==Derivasjon av trigonometriske funksjoner== | ||
I denne seksjonen finner du beviser for formlene for derivasjon av de trigonometriske funksjonene. | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
:'''Derivasjon av sin x''' | |||
::<math>\frac{d}{dx}\sin\,x=\lim_{\Delta x\to0}\frac{\sin(x+\Delta x)-\sin\,x}{\Delta x}</math> | |||
:Vi bruker sumformelen for sinus og ekspanderer den venstre sinusfunksjonen. | |||
::<math>\lim_{\Delta x\to0}\frac{\sin\,x\,\cos\,\Delta x + \cos\,x\,\sin\,\Delta x-\sin\,x}{\Delta x}</math> | |||
:Vi faktoriserer: | |||
::<math>\lim_{\Delta x\to0}\frac{\sin\,x\,\left(\cos\,\Delta x-1\right) + \cos\,x\,\sin\,\Delta x}{\Delta x}</math> | |||
:Vi har nå en sum av to genseverdier: | |||
::<math>\lim_{\Delta x\to0}\sin\,x\frac{\cos\,\Delta x-1}{\Delta x} + \cos\,x\frac{\sin\,\Delta x}{\Delta x}</math> | |||
:Det kan bevises geometrisk at | |||
::<math>\lim_{\Delta x\to0}\frac{\cos\,\Delta x-1}{\Delta x}=0</math> | |||
:og at | |||
::<math>\lim_{\Delta x\to0}\frac{\sin\,\Delta x}{\Delta x}=1</math> | |||
:Resultatet blir da at | |||
::<math>\frac{d}{dx}\sin\,x=\cos\,x</math> | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
:'''Derivasjon av cos x''' | |||
::<math>\frac{d}{dx}\cos\,x=\lim_{\Delta x\to0}\frac{\cos(x+\Delta x)-\cos\,x}{\Delta x}</math> | |||
:Vi bruker sumformelen og ekspanderer den venstre cosinusfunksjonen. | |||
::<math>\lim_{\Delta x\to0}\frac{\cos\,x\,\cos\,\Delta x-\sin\,x\,\sin\,\Delta x-\cos\,x}{\Delta x}</math> | |||
:Vi faktoriserer. | |||
::<math>\lim_{\Delta x\to0}\frac{\cos\,x\,\left(\cos\,\Delta x-1\right)-\sin\,x\,\sin\,\Delta x}{\Delta x}</math> | |||
:Vi har nå en sum av to grenseverdier: | |||
::<math>\lim_{\Delta x\to0}\cos\,x\frac{\cos\,\Delta x-1}{\Delta x}-\sin\,x\frac{\sin\,\Delta x}{\Delta x}</math> | |||
:Disse grenseverdiene er de samme som vi støtte på i beviset av derivasjonen av sinusfunksjonen. Dermed blir resultatet at | |||
::<math>\frac{d}{dx}\cos\,x=-\sin\,x</math> | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
:'''Derivasjon av tan x''' | |||
:Nå som vi har derivasjonsformlene for sinus og cosinusfunksjonene, kan vi derivere tangensfunksjonen. Til det bruker vi definisjonen av tangens og skriver den som en brøk av sinus og cosinus og bruker brøkregelen. | |||
::<math>\frac{d}{dx}\tan\,x=\frac{d}{dx}\frac{\sin\,x}{\cos\,x}=\frac{\left(\frac{d}{dx}\sin\,x\right)\cos\,x-\left(\frac{d}{dx}\cos\,x\right)\sin\,x}{\cos^2x}=\frac{\cos^2x+\sin^2x}{\cos^2x}</math> | |||
:Vi nevnte i seksjonen om trigonometriske identiteter at vi skulle bevise identiteten om tangens og cosinus. Det gjør vi nå. Det er to måter å forenkle brøken over på. Den ene er å trekke sammen sinus og cosinus med <math>\sin^2x+\cos^2x=1</math>. Den andre er å separere brøken. | |||
::<math>\frac{\cos^2x+\sin^2x}{\cos^2x}=\frac{1}{\cos^2x}</math> | |||
::<math>\frac{\cos^2x+\sin^2x}{\cos^2x}=\frac{\sin^2x}{\cos^2x}+\frac{\cos^2x}{\cos^2x}=\tan^2x+1</math> | |||
:Ettersom disse uttrykkene åpenbart må være like, har vi bevist identiteten. | |||
:Resultatet av derivasjonen er | |||
::<math>\frac{d}{dx}\tan\,x=\tan^2x+1</math> | |||
:og | |||
::<math>\frac{d}{dx}\tan\,x=\frac{1}{\cos^2x}</math> | |||
</div> | |||
---- | ---- | ||
[[R2 Hovedside|Tilbake til R2 Hovedside]] | [[R2 Hovedside|Tilbake til R2 Hovedside]] | ||
[[kategori:lex]] | |||
[[Kategori:R2]] | [[Kategori:R2]] | ||
[[Kategori:Geometri]] | [[Kategori:Geometri]] | ||
[[Kategori:Analyse]] | [[Kategori:Analyse]] | ||
[[Kategori:Ped]] | [[Kategori:Ped]] | ||
Siste sideversjon per 21. okt. 2019 kl. 12:46
Absolutt vinkelmål
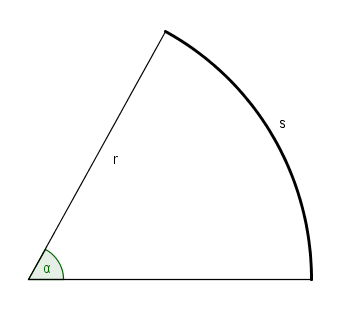
Radianer (også kalt absolutt vinkelmål) er definert som følger. Ta utgangspunkt i figuren:
Vi konstruerer en sirkelbue med lengde <math>s</math> og radius <math>r</math>, som vist på figuren. Buen er avgrenset av de to radiene som går fra sentrum av buen. Vinkelen mellom de to radiene i radianer er da definert som
$$\alpha=\frac{s}{r}$$
Det følger at forholdet mellom radianer og grader er gitt ved
- <math>360^\circ=2\pi</math>
eller ekvivalent ved
- <math>v[^\circ]=\frac{180^\circ}{\pi}v[\text{rad}]</math> for en vinkel <math>v</math>
Trigonometeriske funksjoner
De tre sentrale trigonometriske funksjonene er sinus, cosinus og tangens, som er et produkt av sinus og cosinus. Sinus er den viktigste trigonometriske funksjonen, siden alle de andre trigonometriske funksjonene kan utledes fra denne.
Enhetssirkelen
Enhetssirkelen har sentrum i origo og radius en.
Definisjon av sin x og cos x
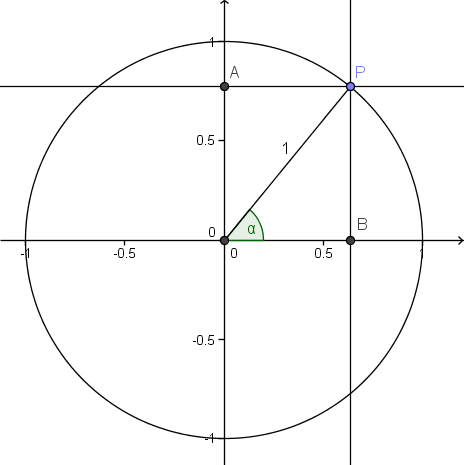
Ta utgangspunkt i figuren under:
Når vi konstruerer en enhetssirkel og en radius med vinkel <math>\alpha</math> på x-aksen slik figuren viser, vil radien skjære sirkelperiferien i punktet <math>P</math>. Hvis trekker normalene fra <math>P</math> på koordinataksene, vil de skjære disse i punktene <math>A</math> og <math>B</math> slik figuren viser. Da vil y-verdien til punktet <math>A</math> være lik <math>\sin\,\alpha</math> og x-verdien til punktet <math>B</math> være lik <math>\cos\,\alpha</math>
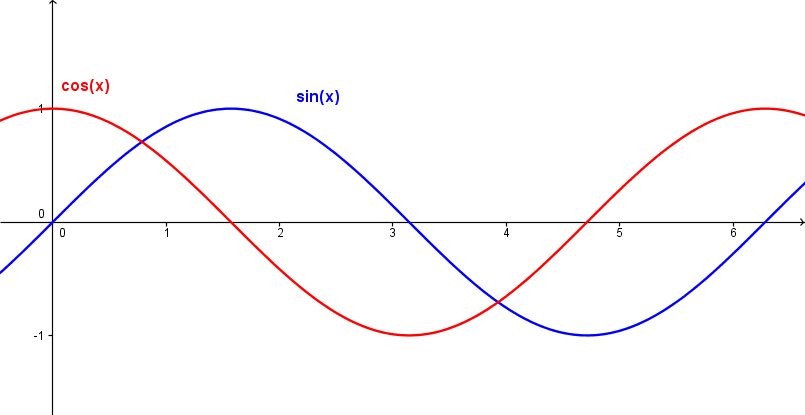
Når vi plotter sinus- og cosinuskurvene ser de slik ut:
Sinus- og cosinuskurvene har begge perioder på <math>2\pi</math> radianer.
Merk at cosinusfunksjonen kun er sinusfunkjsonen forskjøvet <math>\frac{\pi}{2}</math> radianer i minusretningen. Altså gjelder det at <math>sin(x+\frac{\pi}{2})=\cos\,x</math>
Definisjon av tan(x)
Tangensfunksjonen er definert slik at
- <math>\tan\,x=\frac{\sin\,x}{\cos\,x}</math>
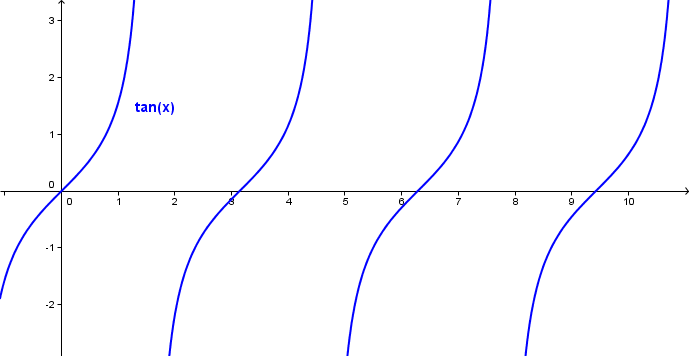
Når vi plotter tangenskurven, ser den slik ut:
Tangenskurven har en periode på <math>\pi</math> radianer.
Fortegn av trigonometriske funksjoner
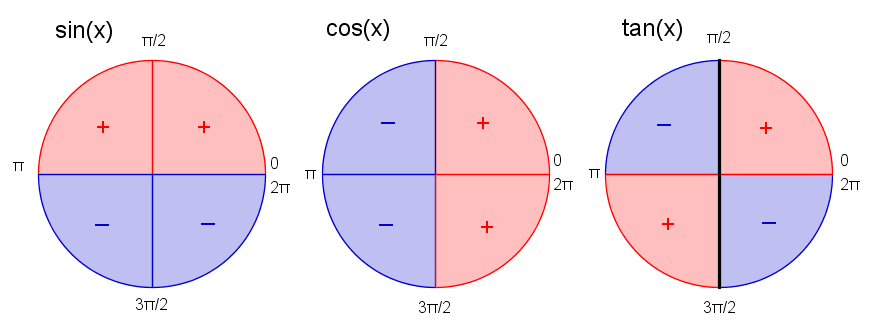
Dette diagrammet viser fortegnene til de forskjellige trigonometriske funksjonene for forskjellige vinkler. Den sorte streken gjennom tangensdiagrammet viser vinklene der <math>\tan\,x</math> går mot <math>\pm\infty</math>. Vi får et bruddpunkt, og det er derfor meningsløst å snakke of fortegnet til <math>\tan\,x</math> når <math>x=\frac{\pi}{2}</math> eller <math>x=\frac{3\pi}{2}</math>.
Hvis du kan disse diagrammene utanat, vil du kunne vurdere hvilke løsninger du forventer til trigonometriske ligninger. Det vil bli lettere å vurdere om løsningene stemmer.
Noen viktige verdier av sin x, cos x og tan x på tabellform
Verdiene i tabellen under bør du memorisere. Å kunne disse utenat vil være til stor hjelp i løsingen av trigonometriske ligninger.
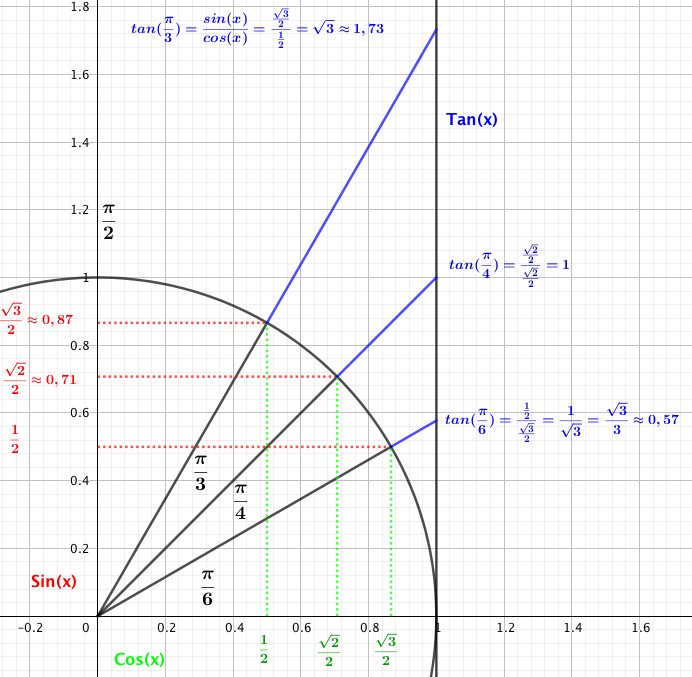
Noen viktige verdier av sin x, cos x og tan x i enhetssirkelen (1. kvadrant)
Viktige trigonometriske identiteter
Ettersom alle de trigonometriske funksjonene er periodiske, vil de samme verdiene gå igjen for hver syklus. Generellt gjelder det at
- <math>\sin(x+2\pi)=\sin\,x</math>
- <math>\cos(x+2\pi)=\cos\,x</math>
- <math>\tan(x+\pi)=\tan\,x</math>
Å være klar over disse sammenhengene vil ha betydning når vi senere vurderer løsninger av trigonometriske ligninger.
Ut ifra figuren om definisjonen av sinus og cosinus kan vi se flere egenskaper ved funksjonene. Spesifikt,
- <math>\sin(\pi-x)=\sin\,x</math>
- <math>\sin(-x)=-\sin\,x</math>
- <math>\cos(2\pi-x)=\cos\,x</math>
- <math>\tan(-x)=-\tan\,x</math>
De trigonometriske funksjonene har mange viktige relasjoner med hverandre. Noe som gjelder per definisjon for sinus og cosinus er identiteten
- <math>\sin^2x+\cos^2x=1</math>
som lett kan vises geometrisk med Pythagorassetningen, se figuren om definisjonen av sinus og cosinus.Denne identiteten er viktig fordi den lar oss omforme sinus til cosinus og omvendt.
Som vi senere skal se, henger også tangens sammen med cosinus på følgende måte:
- <math>\tan^2x+1=\frac{1}{\cos^2x}</math>
Denne identiteten beviser vi lenger nede i artikkelen.
Inverse trigonometriske funksjoner
Vi definerer de inverse trigonometriske funksjonene <math>\arcsin</math>, <math>\arccos</math> og <math>\arctan</math> slik at
- <math>\arcsin(\sin\,x)=x\,,\,x\in [-\frac{\pi}{2},\frac{\pi}{2}]</math>
- <math>\arccos(\cos\,x)=x\,,\,x\in [0,\pi]</math>
- <math>\arctan(\tan\,x)=x\,,\,x\in <-\frac{\pi}{2},\frac{\pi}{2} ></math>
Dersom <math>x</math> ikke befinner seg i disse mengdene, vil du likevel få en verdi innenfor disse mengdene. Ha dette i bakhodet når du løser trigonometriske ligninger på kalkulator.
I mange lærebøker i den videregående skole, og på kalkulatoren er notasjonen slik:
<math>arcsinx = sin^{-1}x\,,\ arccos x = cos^{-1} x \,,\ arctan x = tan^{-1} x</math>
Sumformelen for sin x og cos x
Hvis vi vet verdien av sinus og cosinus til to forskjellige vinkler, kan vi finne sinus og cosinus til summen av vinklene. Vi vet at
- <math>\sin(v\pm u)=\sin\,v\,\cos\,u\pm\cos\,v\,\sin\,u</math>
og
- <math>\cos(v\pm u)=\cos\,v\,\cos\,u\mp \sin\,v\,\sin\,u</math>
Også disse identitetene kan bevises geometrisk.
Spesialtilfellet <math>u=v</math> er verdt å merke seg, siden disse av og til dukker opp i ligninger:
- <math>\sin(2v)=2\sin\,v\,\cos\,v</math>
- <math>\cos(2v)=\cos^2v-\sin^2v</math>
Trigonometriske ligninger
Trigonometriske ligninger er ligninger der trigonometriske funksjoner av variabler inngår. Disse er nyttige i mange abstrakte og fysiske situasjoner.
I denne seksjonen presenteres løsningsmetoder for de forskjellige typene trigonometriske ligninger.
Løsninger og definisjonsmengde
I mange trigonometriske ligninger er definisjonsmengden til variabelen gitt på forhånd. Definisjonsmengden har innflytelse ikke bare på hva løsningene er, men også hvor mange løsninger som finnes. Dersom det ikke er gitt noen definisjonsmengde kan variabelen ha enhver reell verdi. For å få med alle løsninger bruker vi et lite triks, som vi viser nedenfor.
Når definisjonsmengden er gitt, bør du først se om du kan forhåndsbestemme hvor mange løsninger du forventer å få. Gitt at ligningen er løselig er det akseptabelt å forvente to løsninger per <math>2\pi</math>-syklus av de trigonometriske funksjonene. Her er et eksempel:
- Eksempel
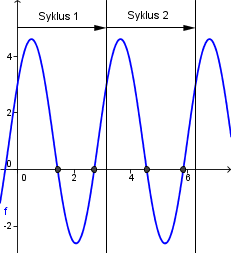
- Bildet viser en plott av funksjonen <math>f(x)=3\sin(2x)+2\cos(2x)+1</math>. Nullpunktene til funksjonen, markert med grå prikker, viser løsningene til ligningen <math>3\sin(2x)+2\cos(2x)=-1</math>. Hvis definisjonsmengden er <math>x\in [0,\pi></math>, går funksjonene gjennom én <math>2\pi</math>-syklus, og vi får 2 løsninger. Hvis definisjonsmengden er <math>x\in [0,2\pi></math>, går funksjonene gjennom to <math>2\pi</math>-sykluser, og nå får vi 4 løsninger.
- OBS!
- Regelen om 2 løsninger per syklus gjelder bare hvis vi kan uttrykke ligningen ved én enkelt trigonometrisk funksjon, og denne ikke har sin største eller minste verdi. Som vi skal se senere kan funksjonen over beskrives på formen <math>f(x)=A\sin(x+\phi)+d</math>.
Derivasjon av trigonometriske funksjoner
I denne seksjonen finner du beviser for formlene for derivasjon av de trigonometriske funksjonene.
- Derivasjon av sin x
- <math>\frac{d}{dx}\sin\,x=\lim_{\Delta x\to0}\frac{\sin(x+\Delta x)-\sin\,x}{\Delta x}</math>
- Vi bruker sumformelen for sinus og ekspanderer den venstre sinusfunksjonen.
- <math>\lim_{\Delta x\to0}\frac{\sin\,x\,\cos\,\Delta x + \cos\,x\,\sin\,\Delta x-\sin\,x}{\Delta x}</math>
- Vi faktoriserer:
- <math>\lim_{\Delta x\to0}\frac{\sin\,x\,\left(\cos\,\Delta x-1\right) + \cos\,x\,\sin\,\Delta x}{\Delta x}</math>
- Vi har nå en sum av to genseverdier:
- <math>\lim_{\Delta x\to0}\sin\,x\frac{\cos\,\Delta x-1}{\Delta x} + \cos\,x\frac{\sin\,\Delta x}{\Delta x}</math>
- Det kan bevises geometrisk at
- <math>\lim_{\Delta x\to0}\frac{\cos\,\Delta x-1}{\Delta x}=0</math>
- og at
- <math>\lim_{\Delta x\to0}\frac{\sin\,\Delta x}{\Delta x}=1</math>
- Resultatet blir da at
- <math>\frac{d}{dx}\sin\,x=\cos\,x</math>
- Derivasjon av cos x
- <math>\frac{d}{dx}\cos\,x=\lim_{\Delta x\to0}\frac{\cos(x+\Delta x)-\cos\,x}{\Delta x}</math>
- Vi bruker sumformelen og ekspanderer den venstre cosinusfunksjonen.
- <math>\lim_{\Delta x\to0}\frac{\cos\,x\,\cos\,\Delta x-\sin\,x\,\sin\,\Delta x-\cos\,x}{\Delta x}</math>
- Vi faktoriserer.
- <math>\lim_{\Delta x\to0}\frac{\cos\,x\,\left(\cos\,\Delta x-1\right)-\sin\,x\,\sin\,\Delta x}{\Delta x}</math>
- Vi har nå en sum av to grenseverdier:
- <math>\lim_{\Delta x\to0}\cos\,x\frac{\cos\,\Delta x-1}{\Delta x}-\sin\,x\frac{\sin\,\Delta x}{\Delta x}</math>
- Disse grenseverdiene er de samme som vi støtte på i beviset av derivasjonen av sinusfunksjonen. Dermed blir resultatet at
- <math>\frac{d}{dx}\cos\,x=-\sin\,x</math>
- Derivasjon av tan x
- Nå som vi har derivasjonsformlene for sinus og cosinusfunksjonene, kan vi derivere tangensfunksjonen. Til det bruker vi definisjonen av tangens og skriver den som en brøk av sinus og cosinus og bruker brøkregelen.
- <math>\frac{d}{dx}\tan\,x=\frac{d}{dx}\frac{\sin\,x}{\cos\,x}=\frac{\left(\frac{d}{dx}\sin\,x\right)\cos\,x-\left(\frac{d}{dx}\cos\,x\right)\sin\,x}{\cos^2x}=\frac{\cos^2x+\sin^2x}{\cos^2x}</math>
- Vi nevnte i seksjonen om trigonometriske identiteter at vi skulle bevise identiteten om tangens og cosinus. Det gjør vi nå. Det er to måter å forenkle brøken over på. Den ene er å trekke sammen sinus og cosinus med <math>\sin^2x+\cos^2x=1</math>. Den andre er å separere brøken.
- <math>\frac{\cos^2x+\sin^2x}{\cos^2x}=\frac{1}{\cos^2x}</math>
- <math>\frac{\cos^2x+\sin^2x}{\cos^2x}=\frac{\sin^2x}{\cos^2x}+\frac{\cos^2x}{\cos^2x}=\tan^2x+1</math>
- Ettersom disse uttrykkene åpenbart må være like, har vi bevist identiteten.
- Resultatet av derivasjonen er
- <math>\frac{d}{dx}\tan\,x=\tan^2x+1</math>
- og
- <math>\frac{d}{dx}\tan\,x=\frac{1}{\cos^2x}</math>