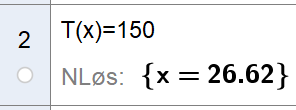1T 2020 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (39 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 9: | Linje 9: | ||
[https://matematikk.net/matteprat/download/file.php?id=3132 Løsningsforslag til del 1 og 2 laget av Svein Arneson] | [https://matematikk.net/matteprat/download/file.php?id=3132 Løsningsforslag til del 1 og 2 laget av Svein Arneson] | ||
[https://youtu.be/lgPLWCsIXX0 Videoløsning del 1 laget av Lektor Lainz] | |||
[https://youtu.be/VVGJh-OOTlE Videoløsning del 2 laget av Lektor Lainz] | |||
=DEL 1= | =DEL 1= | ||
| Linje 78: | Linje 83: | ||
==Oppgave 6== | ==Oppgave 6== | ||
$\frac{\sqrt{45}+\sqrt{80}}{\sqrt{125}}$ | |||
$=\frac{\sqrt{9\cdot 5}+\sqrt{16\cdot 5}}{\sqrt{25\cdot 5}}$ | |||
$=\frac{3\sqrt{5}+4\sqrt{5}}{5\sqrt{5}}$ | |||
$=\frac{7\sqrt{5}}{5\sqrt{5}}$ | |||
$=\frac{7}{5}$ | |||
==Oppgave 7== | |||
$9^2\cdot 3^{-3}\cdot 8^{\frac{1}{3}}\cdot 27^{-\frac{2}{3}}$ | |||
$=(3^2)^2\cdot 3^{-3}\cdot (2^3)^{\frac{1}{3}}\cdot (3^3)^{-\frac{2}{3}}$ | |||
$=3^4\cdot 3^{-3}\cdot 2^1\cdot3^{-2}$ | |||
$=3^{4-3-2}\cdot 2$ | |||
$=3^{-1} \cdot 2$ | |||
$=\frac{2}{3}$ | |||
==Oppgave 8== | |||
$lg10+lg0,1+lg\frac{1}{100}+lg\sqrt[3]{10}$ | |||
$=1+(-1)+(-2)+\frac{1}{3}lg10$ | |||
$=-2+\frac{1}{3}\cdot 1$ | |||
$=\frac{-6}{3}+\frac{1}{3}$ | |||
$=-\frac{5}{3}$ | |||
==Oppgave 9== | |||
===a)=== | |||
$lg(\frac{3x+3}{3})=3$ | |||
$\frac{3x+3}{3}=10^3$ | |||
$3x+3 = 1000\cdot 3$ | |||
$3x = 3000-3$ | |||
$x = \frac{2997}{3}$ | |||
$x = 999$ | |||
===b)=== | |||
$3^{x^2}\cdot 3^{-4x}=1$ | |||
$3^{x^2-4x}=3^0$ | |||
$x^2-4x=0$ | |||
$x(x-4)=0$ | |||
$x=0 \vee x=4$ | |||
==Oppgave 10== | |||
Arealet av det skraverte området kan uttrykkes ved: | |||
1) $(a-b)(a-b)=(a-b)^2$ | |||
2) $a^2-ab-ab+b^2=a^2-2ab+b^2$ | |||
Figuren illustrerer andre kvadratsetning. | |||
==Oppgave 11== | |||
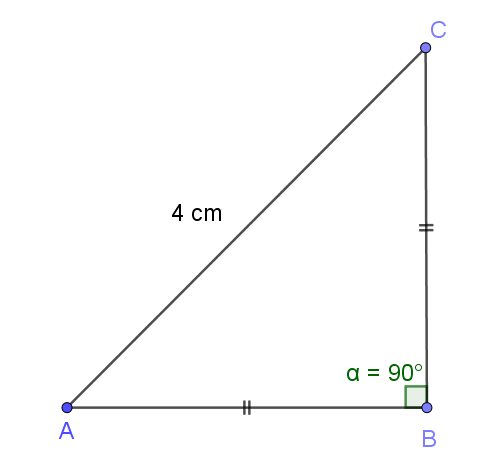
Siden $tan\angle A = 1$, er katetene i denne rettvinklede trekanten like store. | |||
[[File: 1T_v20_11.png]] | |||
Brukes Pytagorassetningen til å finne lengden av katetene, AB og BC, som er like store: | |||
$x^2+x^2=4^2$ | |||
$2x^2 = 16$ | |||
$x^2 = 8$ | |||
$x=\sqrt{8} = 2\sqrt{2}$ | |||
$AB = BC = 2\sqrt{2}$ | |||
==Oppgave 12== | |||
$P(2,4)+P(4,2)= \frac{1}{10}\cdot \frac{1}{10} + \frac{1}{10}\cdot \frac{1}{10} = \frac{1}{100}+\frac{1}{100} = \frac{2}{100} = 0,02$ | |||
Sannsynligheten for at koden begynner på 2 4 eller 4 2 er 0,02. | |||
==Oppgave 13== | |||
===a)=== | |||
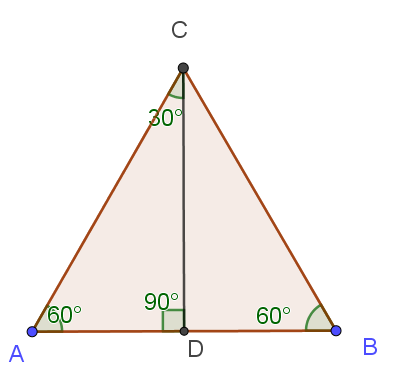
Vi lager en midtnormal på AB, slik at vi får trekanten ADC. I en trekant der vinklene er $30^{\circ}, 60^{\circ}$ og $90^{\circ}$, er den korteste kateten halvparten av lengden til hypotenusen. | |||
[[File: 1T_v20_13a2.png]] | |||
Vi har da: | |||
$sin \angle DCA = \frac{AD}{AC}$ | |||
$sin30^{\circ} = \frac{1}{2}$ | |||
Hvilket skulle vises. | |||
===b)=== | |||
Bruker cosinussetningen til å bestemme lengden av QR: | |||
$QR^2=PR^2+PQ^2-2\cdot PR \cdot PQ \cdot cos\angle P$ | |||
$QR^2 = 5^2+8^2-2\cdot 5\cdot 8 \cdot cos60^{\circ}$ | |||
$QR^2 = 25+64-80\cdot \frac{1}{2}$ | |||
$QR^2 = 89-40$ | |||
$QR = \sqrt{49}$ | |||
$QR = 7$ | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
Hvis du ikke husker at $cos60^{\circ} = \frac{1}{2}$, kan du bruke figuren i a). Vi har da: | |||
$cos\angle A = \frac{AD}{AC}$ | |||
$cos60^{\circ}=\frac{1}{2}$ | |||
</div> | |||
==Oppgave 14== | |||
1) Funksjonen <i>p</i> er en tredjegradsfunksjon, så den deriverte må være en andregradsfunksjon, figur 2 eller 6. Funksjonen <i>p</i> synker i området mellom topp- og bunnpunktet, og da må den deriverte være negativ (under x-aksen) i dette området. Det passer med at <b> figur 2 viser grafen til den deriverte til funksjonen <i>p</i> </b>. | |||
2) Funksjonen <i>q</i> er en lineær funksjon, så den deriverte må være en konstant, slik som grafen i figur 4. I tillegg ser vi at funksjonsuttrykket til <i>q</i> er $y=\frac{1}{2} x$. Den deriverte vil være $y=\frac{1}{2}$, som stemmer med grafen i figur 4. <b> Figur 4 viser grafen til den deriverte til funksjonen <i>q</i> </b>. | |||
3) Funksjonen <i>r</i> er en andregradsfunksjon, så den deriverte må være en lineær funksjon, slik som grafen i figur 5. Det stemmer også med at bunnpunktet på grafen til funksjonen <i>r</i> er nullpunktet på grafen i figur 5. <b> Figur 5 viser grafen til den deriverte til funksjonen <i>r</i> </b>. | |||
4) Funksjonen <i>s</i> er en eksponentialfunksjon som synker for alle verdier av x, og går mot null når x går mot uendelig. Den deriverte vil være en eksponentialfunksjon hvor funksjonsverdien er negativ for alle verdier av x, men nærmer seg null når x går mot uendelig. Det passer med at <b> figur 3 viser grafen til den deriverte til funksjonen <i>s</i> </b>. | |||
==Oppgave 15== | |||
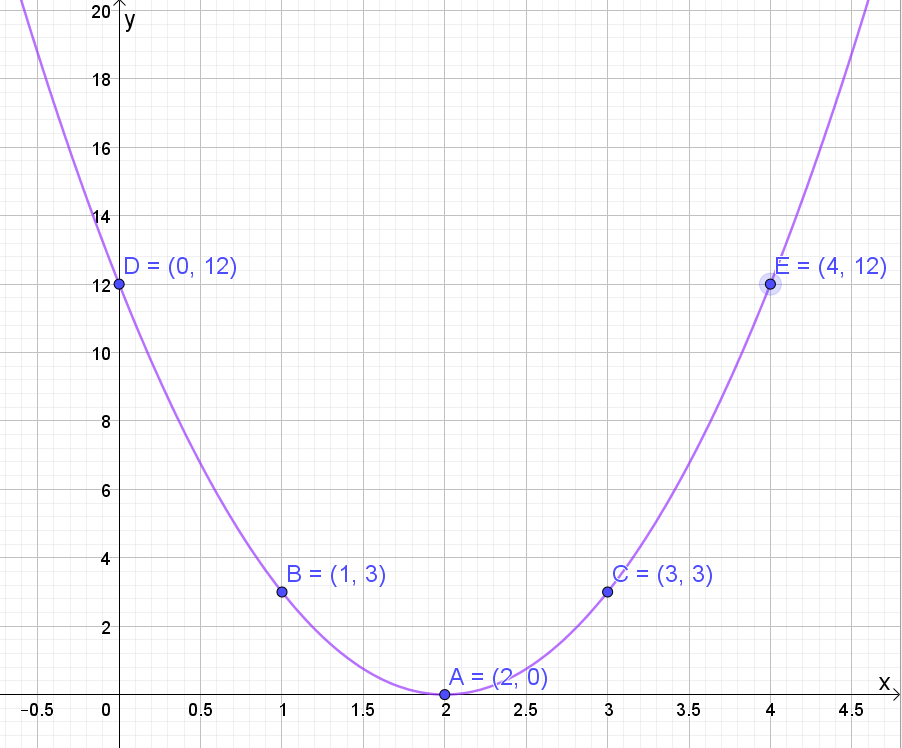
Funksjonen <i>f</i> er en tredjegradsfunksjon, og vi vet derfor at den deriverte av <i>f</i> er en andregradsfunksjon. | |||
Funksjonen <i>f</i> har et terrassepunkt i x=2, derfor er f'(2)=0. Den deriverte har punktet (2,0), som også er bunnpunktet til den deriverte. Den deriverte er derfor symmetrisk om linja x=2. | |||
Stigningstallet til tangenten til grafen til <i>f</i> er 3 når x=1. Den deriverte har derfor punktet (1,3), og også punktet (3,3) på grunn av symmetri om linja x=2. | |||
Stigningstallet til tangenten til grafen til <i>f</i> er 12 når x=4. Den deriverte har derfor punktet (4,12), og også punktet (0,12) på grunn av symmetri om linja x=2. | |||
[[File: 1T_v20_15.png]] | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
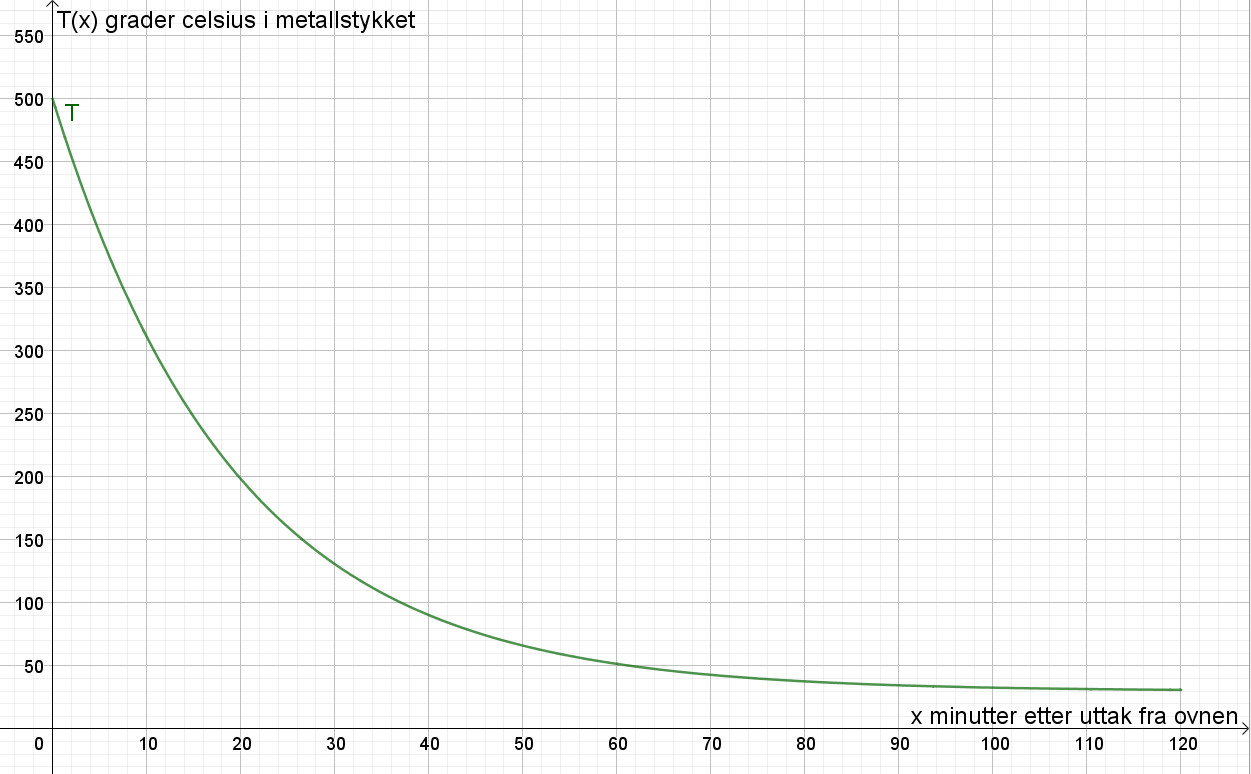
Bruker Geogebra til å tegne grafen til <i>T</i>. | |||
[[File: 1T_v20_1a.png]] | |||
===b)=== | |||
Bruker CAS i Geogebra til å løse oppgaven. | |||
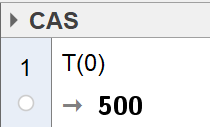
[[File: 1T_v20_1b.png]] | |||
Temperaturen i metallstykket er 500 grader celsius når smeden tar det ut av ovnen. | |||
===c)=== | |||
[[File: 1T_v20_1c2.png]] | |||
Smeden har omtrent 26 minutter på å bearbeide metallstykket etter at han har tatt det ut av ovnen. | |||
===d)=== | |||
[[File: 1T_v20_1d.png]] | |||
$A=394 \\ B=-18,7 \\ C=23 \\ D=174$ | |||
==Oppgave 2== | |||
===a)=== | |||
{| width="auto" | |||
| | |||
|Maskin A | |||
|Maskin B | |||
|Sum | |||
|- | |||
|Feil | |||
| $0,05\cdot 200=10$ | |||
| $0,02\cdot 100=2$ | |||
| $10+2=12$ | |||
|- | |||
|Ikke feil | |||
|$0,95\cdot 200=190$ | |||
|$0,98\cdot 100=98$ | |||
|$190+98=288$ | |||
|- | |||
|Sum | |||
|$200$ | |||
|$100$ | |||
|$300$ | |||
|} | |||
===b)=== | |||
$P(feil) = \frac{12}{300}=0,04$ | |||
Sannsynligheten for at det er feil ved hengelåsen er 0,04. | |||
===c)=== | |||
$P(maskin A | feil) = \frac{10}{12}=0,83$ | |||
Sannsynligheten for at hengelåsen er produsert av maskin A er 0,83. | |||
==Oppgave 3== | |||
===a)=== | |||
$f(x)=ax^3-bx-2$ | |||
$f'(x)=3ax^2-b$ | |||
At grafen til <i>f</i> har topppunkt i x=2 betyr at den deriverte til <i>f</i> har verdien 0 i x=2. | |||
$f'(2)=0 \\ 3a\cdot 2^2-b=0 \\ 12a-b=0$ | |||
At grafen til <i>f</i> har topppunkt i (2,6) betyr at <i>f</i> har verdien 6 i x=2. | |||
$f(2)=6 \\ a\cdot 2^3 - b\cdot 2 - 2 = 6 \\ 8a-2b-2=6$ | |||
===b)=== | |||
Bruker CAS i Geogebra til å løse likningssettet. | |||
[[File: 1T_v20_3b.png]] | |||
$a=-\frac{1}{2}$ og $b=-6$ | |||
==Oppgave 4== | |||
Bruker CAS i Geogebra til å løse oppgaven. | |||
Bruker cosinussetningen i linje 1 til å finne <i>cosA</i>. | |||
Finner vinkel A i linje 2, som jeg har bruk for i linje 3. | |||
Bruker sinussetningen i linje 3 for å finne <i>sinC</i>. | |||
[[File:1T_v20_4.png]] | |||
==Oppgave 5== | |||
===a)=== | |||
Bruker CAS i Geogebra til å løse oppgaven. Bruker definisjonen av sinus. | |||
[[File: 1T_v20_5a2.png]] | |||
===b)=== | |||
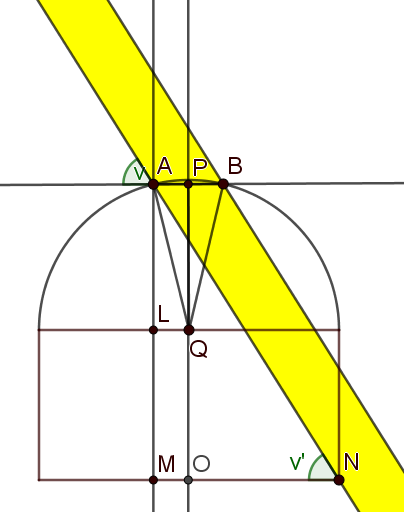
Bruker CAS i Geogebra til å løse oppgaven. Figuren er for å støtte forklaringen. | |||
[[File: 1T_v20_5b2.png]] | |||
[[File: 1T_v20_5b3.png]] | |||
Linje 1 i CAS: finner PQ=21,18, som er lik AL. | |||
Linje 2: finner AM, som er lik AL+ LM. LM er høyden av sylinderen, som er lik radius i halvkulen, som er lik 21,65. | |||
Linje 3: finner MN, som er lik MO + ON. MO er lik AP, som vi fant i a) er 4,5. ON er lik radius i halvkulen, som er lik 21,65. | |||
Linje 4: finner vinkel v', som er lik vinkel v. Disse er samsvarende vinkler. | |||
Løsning: vinkelen v må være minst 58,59 grader for at solstråler skal treffe gulvet i Pantheon. | |||
Siste sideversjon per 15. nov. 2020 kl. 14:16
Diskusjon av denne oppgaven på matteprat
Løsningsforslag til del 1 laget av Kristian Saug
Løsningsforslag til del 2 laget av Kristian Saug
Løsningsforslag til del 1 og 2 laget av Svein Arneson
Videoløsning del 1 laget av Lektor Lainz
Videoløsning del 2 laget av Lektor Lainz
DEL 1
Oppgave 1
$\frac{5,5\cdot 10^{-7}+0,4\cdot 10^{-6}}{0,005} \\= \frac{5,5\cdot 10^{-7}+4\cdot 10^{-7}}{0,005} \\= \frac{(5,5+4)\cdot 10^{-7}}{5\cdot 10^{-3}} \\= \frac{9,5\cdot 10^{-7}}{5\cdot 10^{-3}} \\= 1,9\cdot 10^{-7-(-3)} \\= 1,9\cdot 10^{-4}$
Et tips for å regne ut $\frac{9,5}{5}$ er å gange teller og nevner med 2, slik at du får 10 i nevner, som er lettere å regne ut:
$\frac{9,5}{5}=\frac{9,5\cdot 2}{5\cdot 2}=\frac{19}{10}=1,9$
Oppgave 2
Finner stigningstallet a:
$a = \frac{y_2-y_1}{x_2-x_1} = \frac{0-6}{4-2} = \frac{-6}{2} = -3$
Finner likningen for linja ved ettpunktsformelen:
$y-y_1 = a(x-x_1) \\ y-0 = -3(x-4) \\ y=-3x+12$
Oppgave 3
Bruker innsetningsmetoden.
Uttrykker likning 1 ved y:
$2x+y=3 \\ y=3-2x$
Setter inn uttrykket for y i likning 2:
$8x-2y=-12 \\ 8x-2(3-2x)=-12 \\ 8x-6+4x=-12 \\ 12x = -12+6 \\ x = \frac{-6}{12} \\ x = - \frac{1}{2}$
Finner verdien av y ved hjelp av uttrykket mitt for y:
$y = 3-2x \\ y= 3-2\cdot(-\frac{1}{2}) \\ y = 3+1 \\ y=4$
Løsning: $x = -\frac{1}{2}$ og $y=4$
Oppgave 4
$\frac{2}{x-2}-\frac{x-4}{x^2-5x+6}$
$=\frac{2}{x-2}-\frac{x-4}{(x-2)(x-3)}$
$=\frac{2(x-3)}{(x-2)(x-3)}-\frac{x-4}{(x-2)(x-3)}$
$=\frac{2x-6-x+4}{(x-2)(x-3)}$
$=\frac{x-2}{(x-2)(x-3)}$
$=\frac{1}{x-3}$
Oppgave 5
$2x^2+12x+18 \leq 0$
$=2(x^2+6x+9) \leq 0$
$=2(x+3)(x+3) \leq 0$
$=2(x+3)^2 \leq 0$
Utrykket $(x+3)^2=0$ for $x= -3$. For alle andre x-verdier er uttrykket positivt.
Den eneste løsningen av ulikheten $2x^2+12x+18 \leq 0$ er $x = -3$.
Oppgave 6
$\frac{\sqrt{45}+\sqrt{80}}{\sqrt{125}}$
$=\frac{\sqrt{9\cdot 5}+\sqrt{16\cdot 5}}{\sqrt{25\cdot 5}}$
$=\frac{3\sqrt{5}+4\sqrt{5}}{5\sqrt{5}}$
$=\frac{7\sqrt{5}}{5\sqrt{5}}$
$=\frac{7}{5}$
Oppgave 7
$9^2\cdot 3^{-3}\cdot 8^{\frac{1}{3}}\cdot 27^{-\frac{2}{3}}$
$=(3^2)^2\cdot 3^{-3}\cdot (2^3)^{\frac{1}{3}}\cdot (3^3)^{-\frac{2}{3}}$
$=3^4\cdot 3^{-3}\cdot 2^1\cdot3^{-2}$
$=3^{4-3-2}\cdot 2$
$=3^{-1} \cdot 2$
$=\frac{2}{3}$
Oppgave 8
$lg10+lg0,1+lg\frac{1}{100}+lg\sqrt[3]{10}$
$=1+(-1)+(-2)+\frac{1}{3}lg10$
$=-2+\frac{1}{3}\cdot 1$
$=\frac{-6}{3}+\frac{1}{3}$
$=-\frac{5}{3}$
Oppgave 9
a)
$lg(\frac{3x+3}{3})=3$
$\frac{3x+3}{3}=10^3$
$3x+3 = 1000\cdot 3$
$3x = 3000-3$
$x = \frac{2997}{3}$
$x = 999$
b)
$3^{x^2}\cdot 3^{-4x}=1$
$3^{x^2-4x}=3^0$
$x^2-4x=0$
$x(x-4)=0$
$x=0 \vee x=4$
Oppgave 10
Arealet av det skraverte området kan uttrykkes ved:
1) $(a-b)(a-b)=(a-b)^2$
2) $a^2-ab-ab+b^2=a^2-2ab+b^2$
Figuren illustrerer andre kvadratsetning.
Oppgave 11
Siden $tan\angle A = 1$, er katetene i denne rettvinklede trekanten like store.
Brukes Pytagorassetningen til å finne lengden av katetene, AB og BC, som er like store:
$x^2+x^2=4^2$
$2x^2 = 16$
$x^2 = 8$
$x=\sqrt{8} = 2\sqrt{2}$
$AB = BC = 2\sqrt{2}$
Oppgave 12
$P(2,4)+P(4,2)= \frac{1}{10}\cdot \frac{1}{10} + \frac{1}{10}\cdot \frac{1}{10} = \frac{1}{100}+\frac{1}{100} = \frac{2}{100} = 0,02$
Sannsynligheten for at koden begynner på 2 4 eller 4 2 er 0,02.
Oppgave 13
a)
Vi lager en midtnormal på AB, slik at vi får trekanten ADC. I en trekant der vinklene er $30^{\circ}, 60^{\circ}$ og $90^{\circ}$, er den korteste kateten halvparten av lengden til hypotenusen.
Vi har da:
$sin \angle DCA = \frac{AD}{AC}$
$sin30^{\circ} = \frac{1}{2}$
Hvilket skulle vises.
b)
Bruker cosinussetningen til å bestemme lengden av QR:
$QR^2=PR^2+PQ^2-2\cdot PR \cdot PQ \cdot cos\angle P$
$QR^2 = 5^2+8^2-2\cdot 5\cdot 8 \cdot cos60^{\circ}$
$QR^2 = 25+64-80\cdot \frac{1}{2}$
$QR^2 = 89-40$
$QR = \sqrt{49}$
$QR = 7$
Hvis du ikke husker at $cos60^{\circ} = \frac{1}{2}$, kan du bruke figuren i a). Vi har da:
$cos\angle A = \frac{AD}{AC}$
$cos60^{\circ}=\frac{1}{2}$
Oppgave 14
1) Funksjonen p er en tredjegradsfunksjon, så den deriverte må være en andregradsfunksjon, figur 2 eller 6. Funksjonen p synker i området mellom topp- og bunnpunktet, og da må den deriverte være negativ (under x-aksen) i dette området. Det passer med at figur 2 viser grafen til den deriverte til funksjonen p .
2) Funksjonen q er en lineær funksjon, så den deriverte må være en konstant, slik som grafen i figur 4. I tillegg ser vi at funksjonsuttrykket til q er $y=\frac{1}{2} x$. Den deriverte vil være $y=\frac{1}{2}$, som stemmer med grafen i figur 4. Figur 4 viser grafen til den deriverte til funksjonen q .
3) Funksjonen r er en andregradsfunksjon, så den deriverte må være en lineær funksjon, slik som grafen i figur 5. Det stemmer også med at bunnpunktet på grafen til funksjonen r er nullpunktet på grafen i figur 5. Figur 5 viser grafen til den deriverte til funksjonen r .
4) Funksjonen s er en eksponentialfunksjon som synker for alle verdier av x, og går mot null når x går mot uendelig. Den deriverte vil være en eksponentialfunksjon hvor funksjonsverdien er negativ for alle verdier av x, men nærmer seg null når x går mot uendelig. Det passer med at figur 3 viser grafen til den deriverte til funksjonen s .
Oppgave 15
Funksjonen f er en tredjegradsfunksjon, og vi vet derfor at den deriverte av f er en andregradsfunksjon.
Funksjonen f har et terrassepunkt i x=2, derfor er f'(2)=0. Den deriverte har punktet (2,0), som også er bunnpunktet til den deriverte. Den deriverte er derfor symmetrisk om linja x=2.
Stigningstallet til tangenten til grafen til f er 3 når x=1. Den deriverte har derfor punktet (1,3), og også punktet (3,3) på grunn av symmetri om linja x=2.
Stigningstallet til tangenten til grafen til f er 12 når x=4. Den deriverte har derfor punktet (4,12), og også punktet (0,12) på grunn av symmetri om linja x=2.
DEL 2
Oppgave 1
a)
Bruker Geogebra til å tegne grafen til T.
b)
Bruker CAS i Geogebra til å løse oppgaven.
Temperaturen i metallstykket er 500 grader celsius når smeden tar det ut av ovnen.
c)
Smeden har omtrent 26 minutter på å bearbeide metallstykket etter at han har tatt det ut av ovnen.
d)
$A=394 \\ B=-18,7 \\ C=23 \\ D=174$
Oppgave 2
a)
| Maskin A | Maskin B | Sum | |
| Feil | $0,05\cdot 200=10$ | $0,02\cdot 100=2$ | $10+2=12$ |
| Ikke feil | $0,95\cdot 200=190$ | $0,98\cdot 100=98$ | $190+98=288$ |
| Sum | $200$ | $100$ | $300$ |
b)
$P(feil) = \frac{12}{300}=0,04$
Sannsynligheten for at det er feil ved hengelåsen er 0,04.
c)
$P(maskin A | feil) = \frac{10}{12}=0,83$
Sannsynligheten for at hengelåsen er produsert av maskin A er 0,83.
Oppgave 3
a)
$f(x)=ax^3-bx-2$
$f'(x)=3ax^2-b$
At grafen til f har topppunkt i x=2 betyr at den deriverte til f har verdien 0 i x=2.
$f'(2)=0 \\ 3a\cdot 2^2-b=0 \\ 12a-b=0$
At grafen til f har topppunkt i (2,6) betyr at f har verdien 6 i x=2.
$f(2)=6 \\ a\cdot 2^3 - b\cdot 2 - 2 = 6 \\ 8a-2b-2=6$
b)
Bruker CAS i Geogebra til å løse likningssettet.
$a=-\frac{1}{2}$ og $b=-6$
Oppgave 4
Bruker CAS i Geogebra til å løse oppgaven.
Bruker cosinussetningen i linje 1 til å finne cosA.
Finner vinkel A i linje 2, som jeg har bruk for i linje 3.
Bruker sinussetningen i linje 3 for å finne sinC.
Oppgave 5
a)
Bruker CAS i Geogebra til å løse oppgaven. Bruker definisjonen av sinus.
b)
Bruker CAS i Geogebra til å løse oppgaven. Figuren er for å støtte forklaringen.
Linje 1 i CAS: finner PQ=21,18, som er lik AL.
Linje 2: finner AM, som er lik AL+ LM. LM er høyden av sylinderen, som er lik radius i halvkulen, som er lik 21,65.
Linje 3: finner MN, som er lik MO + ON. MO er lik AP, som vi fant i a) er 4,5. ON er lik radius i halvkulen, som er lik 21,65.
Linje 4: finner vinkel v', som er lik vinkel v. Disse er samsvarende vinkler.
Løsning: vinkelen v må være minst 58,59 grader for at solstråler skal treffe gulvet i Pantheon.