1P 2021 Høst eksempeloppgave LK20 LØSNING: Forskjell mellom sideversjoner
| (7 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 14: | Linje 14: | ||
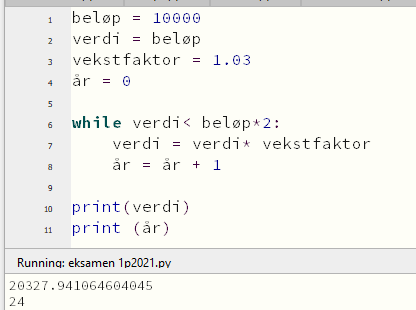
Programmet regner ut hvor lang tid (år) det tar for å doblet et beløp på 10 000, når veksten er 3% per tidsperiode. | Programmet regner ut hvor lang tid (år) det tar for å doblet et beløp på 10 000, når veksten er 3% per tidsperiode. | ||
Linje 10 og 11 skriver ut resultatet: | |||
[[File:081121-01.png ]] | |||
Dersom man ønsker utskrift av årlig endring setter man print kommandoene inn i løkken slik: | |||
[[File:081121-02.png]] | |||
===Oppgave 4=== | ===Oppgave 4=== | ||
| Linje 73: | Linje 80: | ||
===Oppgave 5=== | ===Oppgave 5=== | ||
===a)=== | |||
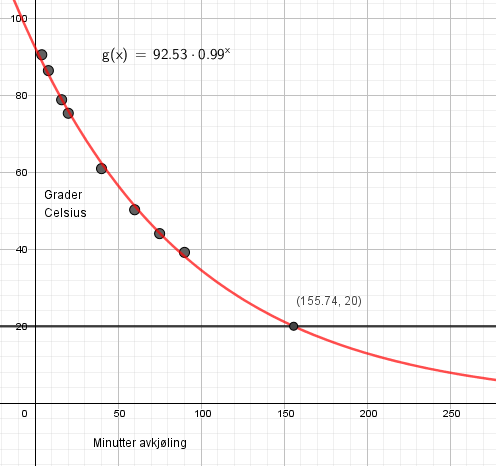
Tallene i | Tallene i tabell en gir oss temperaturen i gelene i avkjølingsforløpet fra 4 minutter til 90 minutter inn i avkjølingen. I dette tidsintervallet er modellen god fordi den følger de faktiske målepunkter godt, $R^2= 0,997 $. Uansett hvor lenge den avkjøles vil den aldri bli kaldere enn romtemperatur, 20 grader celsius. | ||
[[File:061121-04.png]] | |||
Modellen over er god i området 4 - 90 minutter. Vi ser fra de siste målingene at avkjølingen (60, 75, 90) begynner å gå saktere enn hva modellen predikerer. Etter som tiden går vil modellen underestimere temperaturen og etter ca. 156 minutter gir modellen oss verdier under romtemperatur, noe som ikke er i samsvar med virkeligheten. | |||
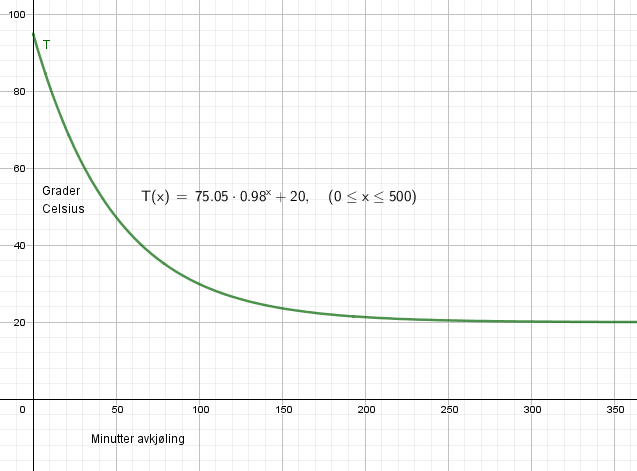
Vi trenger en modell som nærmere seg romtemperatur når tiden blir stor. Stine trekker fra 20 grader på alle målingen. Kjører man regresjon på tabell to i oppgaven får man et utrykk som dette $f(x)=75,05 \cdot 0,98^x$. Dersom vi plusser på romtemperaturen får vi | |||
[[File:081121-04.png]] | |||
===b)=== | |||
Modellen er gyldig så lenge romtemperaturen er stabil. | |||
===Oppgave 6=== | ===Oppgave 6=== | ||
| Linje 92: | Linje 111: | ||
===Oppgave 7=== | ===Oppgave 7=== | ||
[[File:131121-01.png]] | |||
[[File:131121-02.png]] | |||
===Oppgave 8=== | ===Oppgave 8=== | ||
Siste sideversjon per 13. nov. 2021 kl. 08:58
DEL EN
Oppgave 1
Ett parti øker oppslutningen fra 5% til 7%. Det er en $\frac{2}{5}= \frac{4}{10} = 40$ % økning.
Oppgave 2
Dersom 4 personer må betale 600 kr. hver, er totalprisen for båten $ 4 \cdot 600 = 2400$. Da må 12 personer betale 200 kr. hver.
Oppgave 3
Programmet regner ut hvor lang tid (år) det tar for å doblet et beløp på 10 000, når veksten er 3% per tidsperiode. Linje 10 og 11 skriver ut resultatet:
Dersom man ønsker utskrift av årlig endring setter man print kommandoene inn i løkken slik:
Oppgave 4
Hypotenusen er 10 dm, altså 1,0 m. Vi bruker pytagoras og finner at AC må være 0,6 meter eller 6 dm. AC er 60 centimeter.
Oppgave 5
a)
Lager to lineære likninger med tallene fra tabellen og trekker dem fra hverandre:
450 = 25a + b
650 =50a + b
-200 = -25 a
a = 8
Da må b være lik 250.
b)
Hageslangen koster 8 kroner meteren, og vogna koster 250 kroner.
DEL TO
Oppgave 1
26 kg appelsiner krever $26 \cdot 5 = 130 $ dl sukker. Det er 13 liter og vekten er $ 13 \cdot 0,8 = 10,4$ kg. Hun trenger 11 pakker sukker.
Oppgave 2
Påstanden er feil. Dersom temperaturer endrer seg med 5 celsiusgrader, endrer den seg med 9 fahrenheit grader. Det ser man fr leddet: $\frac9 5 \cdot C$.
Oppgave 3
x er poster som gir 2 poeng.
y er poster som gir 5 poeng. Vi får:
$x+y = 13 $
$2x + 5y = 38$
$2x +5(13 -x) = 38$
$2x -5x= 38-65$
$3x = 27$
x= 9
Ni poster gir 2 poeng.
Oppgave 4
Dersom x er mindre enn null er x et negativt tall. Ganget med seg selv, $x^2$ vil alltid gi et positivt tall. Tre negative tall vil alltid gi et negativt svar. Derfor er $x^2 > x^3$ når x er et negativt tall.
Oppgave 5
a)
Tallene i tabell en gir oss temperaturen i gelene i avkjølingsforløpet fra 4 minutter til 90 minutter inn i avkjølingen. I dette tidsintervallet er modellen god fordi den følger de faktiske målepunkter godt, $R^2= 0,997 $. Uansett hvor lenge den avkjøles vil den aldri bli kaldere enn romtemperatur, 20 grader celsius.
Modellen over er god i området 4 - 90 minutter. Vi ser fra de siste målingene at avkjølingen (60, 75, 90) begynner å gå saktere enn hva modellen predikerer. Etter som tiden går vil modellen underestimere temperaturen og etter ca. 156 minutter gir modellen oss verdier under romtemperatur, noe som ikke er i samsvar med virkeligheten.
Vi trenger en modell som nærmere seg romtemperatur når tiden blir stor. Stine trekker fra 20 grader på alle målingen. Kjører man regresjon på tabell to i oppgaven får man et utrykk som dette $f(x)=75,05 \cdot 0,98^x$. Dersom vi plusser på romtemperaturen får vi
b)
Modellen er gyldig så lenge romtemperaturen er stabil.
Oppgave 6
a)
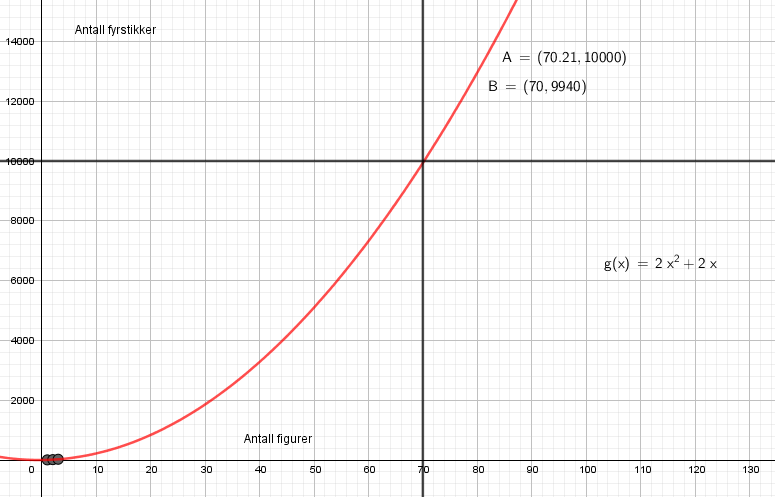
Bruker regresjon, finner et funksjonsuttrykk og ser at man kan lage 70 figurer.
b)
Man får 60 fyrstikker tilovers.
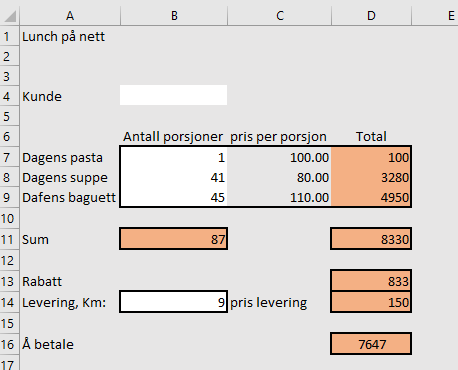
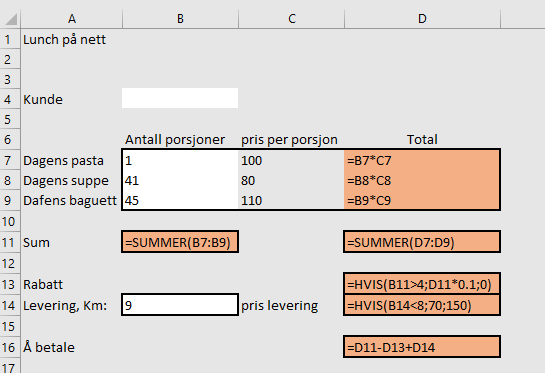
Oppgave 7
Oppgave 8
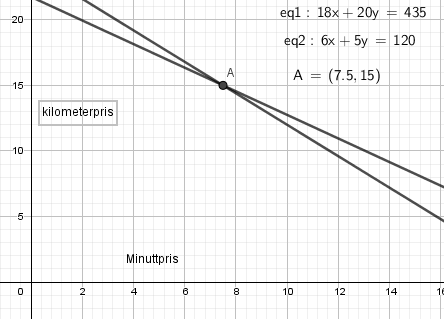
Taxi A tar en startpris på 75 kroner, i tillegg til en minuttpris på 7 kr / minutt og 14 kr / km.
Taxi B
Vi ser at prisen er kr 7,50 per minutt og 15 kr/km. I tillegg er startprisen kr 66.
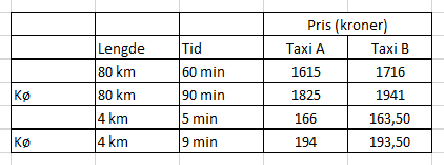
De ser ikke ut til å være stor prisforskjell på selskapene, men la oss sette opp fire senarioer. Langtur med og uten kø. Svipptur med og uten kø.
På korte turer er det i praksis liten forskjell, men på lengre turer er det litt å spare på å velge Taxi A.