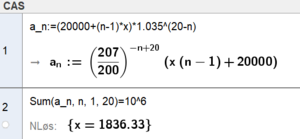Rekker: Forskjell mellom sideversjoner
| (14 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
===Følger=== | ====Følger==== | ||
| Linje 34: | Linje 34: | ||
</div> | </div> | ||
{{Reklame}} | |||
====Eksplisitte uttrykk==== | ====Eksplisitte uttrykk==== | ||
| Linje 56: | Linje 58: | ||
</div> | </div> | ||
====Rekursive uttrykk==== | ====Rekursive uttrykk==== | ||
| Linje 91: | Linje 96: | ||
</div> | </div> | ||
=== Konvergens === | |||
==== Konvergens ==== | |||
Vi sier at en følge <math>(a_n)_{n\in\mathbb{N}}</math> konvergerer mot et element <math>a</math> dersom <math>\lim\limits_{n\to\infty}a_n=a</math>. En aritmetisk følge vil derfor ikke konvergere siden den vokser ubegrenset. | Vi sier at en følge <math>(a_n)_{n\in\mathbb{N}}</math> konvergerer mot et element <math>a</math> dersom <math>\lim\limits_{n\to\infty}a_n=a</math>. En aritmetisk følge vil derfor ikke konvergere siden den vokser ubegrenset. | ||
| Linje 102: | Linje 111: | ||
</div> | </div> | ||
==Rekker== | ====Rekker==== | ||
Dersom man setter pluss eller minus (eller en blanding) får man en rekke. Rekker består av ledd med tall. | Dersom man setter pluss eller minus (eller en blanding) får man en rekke. Rekker består av ledd med tall. | ||
===De naturlige tallene=== | ====De naturlige tallene==== | ||
1, 2, 3, 4 ,5, ...... | 1, 2, 3, 4 ,5, ...... | ||
| Linje 135: | Linje 144: | ||
$a_{n+1} = a_n +1$ | $a_{n+1} = a_n +1$ | ||
{{Reklame}} | |||
===Kvadrater=== | ===Kvadrater=== | ||
| Linje 160: | Linje 172: | ||
$a_{n+1} = ( \sqrt{a_n} +1)^2 = a_n + 2 \sqrt{a_n} +1 = a_n + 2n+1$ | $a_{n+1} = ( \sqrt{a_n} +1)^2 = a_n + 2 \sqrt{a_n} +1 = a_n + 2n+1$ | ||
===Trekanter=== | ====Trekanter==== | ||
Rekken | Rekken | ||
| Linje 170: | Linje 182: | ||
Eksplisit formel: $a_n = \frac {n(n+1)}{2}$ og rekursiv formel : $a_{n+1} = a_n + n +1$. | Eksplisit formel: $a_n = \frac {n(n+1)}{2}$ og rekursiv formel : $a_{n+1} = a_n + n +1$. | ||
===Rektangeler=== | ====Rektangeler==== | ||
| Linje 202: | Linje 214: | ||
En aritmetisk rekke er summen av leddene <math>a_i</math> i en aritmetisk progresjon <math>\{a_i\}_{i\in\mathbb{N}}</math> med et endelig antall ledd <math>N</math>. Den <math>n</math>-te partialsummen(delsummen) er summen av de <math>n\leq N</math> første leddene i rekken og kan defineres ved at <math>S_n=\sum_{i=1}^{n}a_i</math>. Siden <math>a_{i+1}=d+a_i</math> for aritmetiske følger, kan vi utlede en lukket form for den aritmetiske rekken av <math>n</math> ledd: | En aritmetisk rekke er summen av leddene <math>a_i</math> i en aritmetisk progresjon <math>\{a_i\}_{i\in\mathbb{N}}</math> med et endelig antall ledd <math>N</math>. Den <math>n</math>-te partialsummen(delsummen) er summen av de <math>n\leq N</math> første leddene i rekken og kan defineres ved at <math>S_n=\sum_{i=1}^{n}a_i</math>. Siden <math>a_{i+1}=d+a_i</math> for aritmetiske følger, kan vi utlede en lukket form for den aritmetiske rekken av <math>n</math> ledd: | ||
\[S_n=\sum_{i=1}^n a_i=a_1+(a_1+d)+(a_1+2d)+...+(a_1+(n-1)d)\] \[=na_1+\sum_{i=1}^n (i-1)d=na_1+d\sum_{i=0}^{n-1} i=na_1+\frac{n(n-1)}{2}d\] | |||
Merk at formelen kun avhenger av startverdien <math>a_1</math> og den konstante differansen <math>d</math>. | Merk at formelen kun avhenger av startverdien <math>a_1</math> og den konstante differansen <math>d</math>. | ||
| Linje 286: | Linje 298: | ||
</div> | </div> | ||
{{Reklame}} | |||
====Variable kvotienter==== | ====Variable kvotienter==== | ||
| Linje 309: | Linje 327: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel 11''' | |||
Vi har rekken | |||
$1 + \frac 1x + \frac{1}{x^2} + \frac{1}{x^3}+ ...$ | |||
$k = \frac{\frac 1x}{1} = \frac 1x$ | |||
Rekka konvergerer når $-1 < \frac 1x < 1 \quad \Rightarrow \quad \frac 1x > -1 \wedge \frac 1x < 1 \quad \Rightarrow \quad x < -1 \wedge x >1$ | |||
Konvergensområde: | |||
$x \in <\leftarrow, -1> \cup < 1, \rightarrow>$ | |||
</div> | </div> | ||
| Linje 318: | Linje 350: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel 12 (eksempeloppgave UDIR Høst 2022- R2)''' | |||
En uendelig geometrisk rekke $b_1 + b_2 + b_3 + ... $konvergere mot 6. | En uendelig geometrisk rekke $b_1 + b_2 + b_3 + ... $konvergere mot 6. | ||
Siste sideversjon per 19. feb. 2025 kl. 07:24
Følger
En tallfølge er en ordnet liste med tall hvor hvert tall er assosiert med et positivt heltall <math>n</math>. Når vi skriver ut elementene etter stigende <math>n</math> får vi en følge. Man kan betrakte en tallfølge som en funksjon fra de positive heltallene <math>\mathbb{Z}^+</math> til de reelle tallene, <math>\mathbb{R}</math>, eventuelt til de komplekse tallene <math>\mathbb{C}</math>.
En følge kan være uendelig lang eller ha et endelig antall elementer.
Eksempel 1
- 1,2,3,4,5
Dette er en endelig følge med 5 elementer.
Eksempel 2
- 2,4,6,8,...
Dette er en uendelig lang følge. De tre prikkene til sist kjennetegner dette.
Eksempel 3
- 1,3,5,...,9
Denne følgen er endelig, men med mindre det er spesifisert vet vi ikke hvor mange elementer følgen består av.
Eksplisitte uttrykk
Følger kan uttrykkes som funksjoner <math>a_n</math> (sammenlign med <math>f(x)</math>), der <math>n</math> er et positivt heltall.
Eksempel 4
- <math>a_n=n\,,\,n\in[3,7]</math>
Skriver vi ut denne følgen, får vi
- 3,4,5,6,7
Eksempel 5
- <math>a_n=n^2</math>
Ettersom definisjonsmengden til <math>n</math> ikke er spesifisert, kan vi gå ut ifra at følgen omfatter alle <math>n\in\mathbb{N}</math>. Skriver vi ut følgen får vi da
- 1,4,9,16,25,...
Rekursive uttrykk
Det er også mulig å definere følger ved å relatere de forskjellige leddene med hverandre. Da får vi ligninger på formen
<math>f(a_n,a_{n-1},...,a_1,a_0,n)=0</math>
Hvis vi sammen med et slikt uttrykk har informasjon om ett av leddene, er følgen entydig bestemt.
Dette kalles et rekursivt uttrykk og vises best gjennom noen eksempler:
Eksempel 6
<math>a_n=a_{n-1}+n\,,\,a_0=0</math> Ettersom ingen opplysninger og definisjonsmengden til <math>n</math> er gitt, kan vi gå ut ifra at følgen dekker alle positive heltallige <math>n</math>. Skriver vi ut følgen og starter fra <math>n=0</math>, får vi
- 0,1,3,6,10,15,...
I denne følgen er hvert ledd <math>a_n</math> summen av de <math>n</math> første heltallene. Dette ser vi også fra det rekursive uttrykket ved at hvert i hvert ledd legges det neste heltallet til summen av de forrige.
Eksempel 7
Følger trenger ikke være bestemt av én funksjon. Forskjellige funksjoner kan bestemme leddene i forskjellige deler av følgen.
$ a_n=\begin{matrix} 0 & \text{if} & n=0 \\ 1 & \text{if} & n=1 \\ a_{n-1}+a_{n-2} & \text{if} & n>1 \end{matrix} $ Hvis vi skriver ut denne følgen og starter fra <math>n=0</math>, får vi
- 0,1,1,2,3,5,8,13,21,34,55,89,144...
Denne følgen kalles Fibonaccifølgen og har mange interessante geometriske og tallteoretiske egenskaper. Blant annet vil forholdet mellom to påfølgende tall gå mot Det gylne snitt når <math>n</math> går mot uendelig.
Konvergens
Vi sier at en følge <math>(a_n)_{n\in\mathbb{N}}</math> konvergerer mot et element <math>a</math> dersom <math>\lim\limits_{n\to\infty}a_n=a</math>. En aritmetisk følge vil derfor ikke konvergere siden den vokser ubegrenset.
Eksempel 8
- Følgen definert ved <math> f_n=\frac{1}{n}</math> konvergerer mot <math>0</math> når <math>n\to\infty</math> siden <math>\lim\limits_{n\to\infty}\frac{1}{n}=0</math>
- Følgen definert ved <math>g_n=\cos(\frac{1}{n})</math> vil konvergere mot <math>1</math> når <math>n\to\infty</math> siden argumentet går mot <math>0</math> og <math>\cos(0)=1</math>.
Rekker
Dersom man setter pluss eller minus (eller en blanding) får man en rekke. Rekker består av ledd med tall.
De naturlige tallene
1, 2, 3, 4 ,5, ......
Rekken blir:
1 + 2 + 3 + 4 + 5 + ............ + n
Leddets verdi er avhengig av posisjon i rekken. Dersom vi ser på ledd nummer fire, så er verdien 4, ledd fem har verdien 5 osv.
Eksplisitt formel
Dersom man uttrykker et ledd ved hjelp av leddets posisjon i rekken kalles det en eksplisitt formel
Den eksplisitte formelen blir da:
$a_n=n$
På den måten kan vi finne verdien til ledd nr. n.
Dersom vi kjenner verdien og plassen til ett ledd kan vi finne det neste. vi vet at ledd nr. n har verdien n. Siden dette er de naturlige tallene er forskjellen mellom to naboledd lik en.
Rekursiv formel
Dersom man uttrykker et ledd ved hjelp av leddet foran, kalles det en rekursiv sammenheng
Den rekursive formelen blir da:
$a_{n+1} = a_n +1$
Kvadrater
Kvadrattallene er:
1, 4, 9 , 16, 25, ..............
Rekken blir :
1+ 4+9+16+25+ .......
Å finne formelen for leddene her er ikke så lett som for de naturlige tallene, fordi verdien til leddene endrer seg med kvadratet av posisjonen.
Rekken kan skrives slik:
$1^2 + 2^2 +3^2 + 4^2+ ..............+ n^2$
Eksplisit formel blir:
$a_n = n^2$
Rekkusivformel:
$a_{n+1} = ( \sqrt{a_n} +1)^2 = a_n + 2 \sqrt{a_n} +1 = a_n + 2n+1$
Trekanter
Rekken
1 + 3 + 6 + 10 + 15 + 21 +......
Representerer trekanttallene.
Eksplisit formel: $a_n = \frac {n(n+1)}{2}$ og rekursiv formel : $a_{n+1} = a_n + n +1$.
Rektangeler
Vi kan ha mange forskjellige. Her er en:
2 + 6 + 12 + 20 + .....
Det første rektangelet har lengde to og bredde en. Det andre lengde tre og bredde to, osv.
Eksplisit formel:
$a_n = (n+1)n = n^2+n$
Rekkusiv formel:
$a_{n+1} = a_n +2n$
Aritmetisk progresjon
En aritmetisk følge er en tallfølge, $\{a_i\}_{i\in\mathbb{N}}\quad$ ($\mathbb{N}=\{1,2,3,...\}$), slik at differansen mellom to påfølgende ledd er konstant; <math>a_{i+1}-a_i=d</math>.
Eksempel 9
- Vi kan definere en spesiell aritmetisk følge ved at <math>a_{i+1}-a_i=2</math>. For at denne følgen skal være unikt bestemt må vi definere en startverdi, f.eks. <math>a_1=3</math>. Følgen <math>\{a_i\}_{i\in\mathbb{N}}</math> er nå entydig bestemt siden formlene over gir at <math>a_2-a_1=a_2-3=2</math>. Dette gir at <math>a_2=2+3=5</math>. Videre er <math>a_3-a_2=a_3-5=2</math>, så <math>a_3=2+5=7</math> osv.
Aritmetisk rekke (sum)
En aritmetisk rekke er summen av leddene <math>a_i</math> i en aritmetisk progresjon <math>\{a_i\}_{i\in\mathbb{N}}</math> med et endelig antall ledd <math>N</math>. Den <math>n</math>-te partialsummen(delsummen) er summen av de <math>n\leq N</math> første leddene i rekken og kan defineres ved at <math>S_n=\sum_{i=1}^{n}a_i</math>. Siden <math>a_{i+1}=d+a_i</math> for aritmetiske følger, kan vi utlede en lukket form for den aritmetiske rekken av <math>n</math> ledd:
\[S_n=\sum_{i=1}^n a_i=a_1+(a_1+d)+(a_1+2d)+...+(a_1+(n-1)d)\] \[=na_1+\sum_{i=1}^n (i-1)d=na_1+d\sum_{i=0}^{n-1} i=na_1+\frac{n(n-1)}{2}d\]
Merk at formelen kun avhenger av startverdien <math>a_1</math> og den konstante differansen <math>d</math>.
Ledd n i en aritmetisk rekke $ \quad \quad a_n = a_1 + (n-1)d$
Sum aritmetisk rekke:
Summen av de n første ledd:
$S_n = n \cdot \frac{a_1+ a_n}{2}$
Alternativt kan vi uttrykke den samme aritmetiske rekken ved <math>S_n=\sum_{i=1}^na_i=\frac{a_1+a_n}{2}n</math>. Ideen her er å finne gjennomsnittsverdien av par av ledd: Første og siste ledd har et gjennomsnitt <math>\frac{a_1+a_n}{2}</math>. Andre og nest siste ledd har samme gjennomsnitt osv. Siden summen består av n ledd der hvert ledd har et gjennomsnitt på <math>\frac{a_1+a_n}{2}</math>, blir summen <math>\frac{a_1+a_n}{2}\cdot n</math>.
Eksempel 10
- La oss se på den endelige følgen <math>(a_i=i)_{i\in [1,10]}=\{1,2,\ldots ,10\}</math> Da blir summen <math>S=\sum_{i=1}^{10}i=\frac{1+10}{2}\cdot 10 = 55</math>
Geometrisk rekke
En geometrisk progresjon <math>(a_n)_{n\in\mathbb{N}}</math> er en tallfølge der hvert tall er et konstant multippel av det forrige, dvs <math>\frac{a_{n+1}}{a_n}=k</math>.
Slike tallfølger kan skrives på formen <math>a_n=a_1k^{n-1}</math>
En geometrisk rekke er summen av elementene i en geometrisk progresjon.
For geometriske rekker:
<math>a_n=a_1k^{n-1}</math>
Sum: <math>S_n=\sum_{i=1}^n a_i=a_1\frac{k^n-1}{k-1}</math>
Bevis for summeformel
Sum av de n første leddene:
$S_n = a + ak + ak^2 + ak^3 + ... + ak^{n-2} + ak^{n-1}$
Vi multipliserer med k:
$kS_n = ak + ak^2 + ak^3 + ak^4 + ... + ak^{n-1} + ak^{n}$
Vi trekke linje en fra linje to:
$kS_n - S_n = ak^n - a$
$S_n(k-1) = a(k^n-1)$
$S_n = a \frac{k^n-1}{k-1}$
Uendelige geometriske rekker
Endelige rekker gir oss en verdi. Uendelige rekker kan enten gå mot en bestemt verdi, eller de kan gå mot uendelig. Dersom en rekke divergerer går summen mot uendelig. Dersom rekken konvergerer har den en endelig sum.
Dersom $\quad -1<k<1 \quad$ i en geometrisk tallfølge $\quad a_n=a_1k^{n-1}\quad$ sier vi at den konvergerer. Det vil si at summen av uendelig mange etterfølgende elementer i følgen har en endelig verdi.
I slike tilfeller er $ \quad \lim\limits_{x \rightarrow \infty} S_n = \lim\limits_{x \rightarrow \infty} \sum_{i = 1}^{n} a_i = \frac{a_1}{1-k}$
Variable kvotienter
Dersom rekken inneholder ledd med x er det ikke åpenbart å se om rekken konvergerer eller divergerer. Den kan gjøre begge deler, avhengig av x verdien. De x verdier som gjør at rekken konvergerer ligger i konvergensområdet, eller konvergensintervallet. I det komplekse plan vil konvergensområdet være en sirkel. Da snakker man om konvergensradius.
En uendelig geometrisk rekke med variable kvotienter:
$\sum_{i=0}^{\infty}a_1 \cdot (k(x))^{i} = a_1 + a_1 \cdot k(x) + a_1 \cdot (k(x))^2 + ...$
konvergerer når
$-1 < k(x) < 1$,
mot
$S(x) = \frac{a_1}{1 - k(x)}$
Eksempel 11
Vi har rekken
$1 + \frac 1x + \frac{1}{x^2} + \frac{1}{x^3}+ ...$
$k = \frac{\frac 1x}{1} = \frac 1x$
Rekka konvergerer når $-1 < \frac 1x < 1 \quad \Rightarrow \quad \frac 1x > -1 \wedge \frac 1x < 1 \quad \Rightarrow \quad x < -1 \wedge x >1$
Konvergensområde:
$x \in <\leftarrow, -1> \cup < 1, \rightarrow>$
Noen (mer eller mindre) praktiske eksempler
Eksempel 12 (eksempeloppgave UDIR Høst 2022- R2) En uendelig geometrisk rekke $b_1 + b_2 + b_3 + ... $konvergere mot 6.
Summen av de seks første leddene er $\frac{38}{9}$
Fra første settning drar vi følgende informasjon: $\frac{b_1}{1-k} =6$.
Fra andre settning har vi: $b_1 \cdot \frac{1-k^6}{1-k} = \frac{38}{9}$
Vi har to likninger med to ukjente og kan sette inn uttrykket for $b_1$ i den første likningen inn i den andre likningen.
$6 \cdot (1-k) \cdot \frac{1-k^6}{1-k} = \frac{38}{9} \Rightarrow \quad-k^6 = \frac{38}{9 \cdot 6} - 1 \Rightarrow \quad k^6 = 1- \frac {19}{27} = \frac {8}{27} = {(\frac 23})^3 \Rightarrow \quad k^2 = \frac 23$
$S_4 = b_1 \cdot \frac{1-k^4}{1-k} = \frac{b_1}{1-k} \cdot (1-(k^2)^2) = 6 \cdot (1- \frac 49) = 6 \cdot \frac 59 = \frac {10}{3}$
Eksempel 12 (Eksamen S2 - høst 23)
Miriam har bestemt seg for å sette inn 20 000 kroner på en konto i begynnelsen av hvert år. Det første sparebeløpet vil hun sette inn i begynnelsen av 2024, det andre beløpet i begynnelsen av 2025, og så videre. Anta at hun får en fast årlig rentesats på 3,5 prosent.
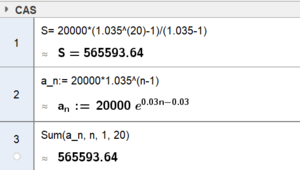
a) Vis at Miriam vil ha 565 594 kroner på kontoen like etter at hun har satt inn innskudd nummer 20.
Løsn.
Vi skal finne sluttbeløpet når vi kjenner innskuddsbeløp og rente.
Dette er en rekke med 20 ledd der $a_1 = 20000$ og k = 1,035
Sum: $S_{20}=20000\frac{1,035^{20}-1}{1,035-1} = 565594$
På Geogebra på to måter:
Hermod har også bestemt seg for å spare. Han vil sette inn et fast beløp i
begynnelsen av hvert år. Det første sparebeløpet setter han inn i begynnelsen av
2024. Han får også en fast årlig rentesats på 3,5 prosent. Hermod har regnet ut
at han vil ha 692 852 kroner på kontoen like etter at innskudd nummer 20 er satt
inn.
b) Bestem beløpet Hermod må sette inn hvert år for at dette skal stemme.
Løsn.
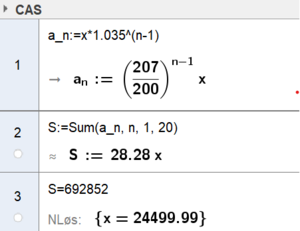
Vi skal finne innskuddsbeløp når vi kjenner sluttbeløp og rente. Vi har fortsatt en geometrisk rekke, med $a_1 = x$ og $k= 1,035$. Vi bruker Geogebra:
Han må spare 24500 kr. hvert år.
Miriam ønsker at det skal være 1 000 000 kroner på kontoen like etter at hun har satt inn innskudd nummer 20. For å få til dette, vil hun øke innskuddet med et fast beløp hvert år. Første innskudd skal være 20 000 kroner.
c) Hvor mye må hun øke innskuddet med hvert år?
Løsn:
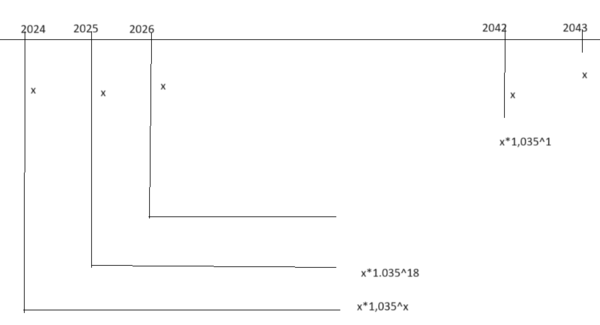
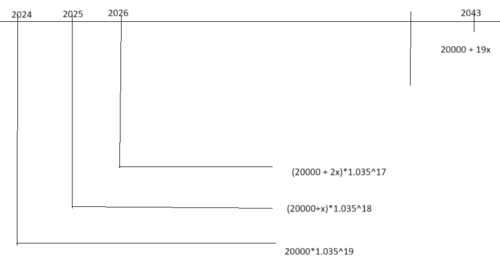
Vi har følgende situasjon:
Dette er en rekke der $a_n = (20000+(n-1)x)\cdot 1.035^{20-n}$
Vi løser med Geogebra:
Hun må årlige øke beløpet med 1836,33 kr.
Eksempel 13 S2- v24
Olivia tar opp et annuitetslån på 2 500 000 kroner for å kjøpe bolig. Hun velger årlige terminer og en nedbetalingstid på 25 år. Det første terminbeløpet skal betales om ett år. Renten er på 5,5 % per år.
a) Hvor store blir de årlige terminbeløpene?
Løsn.
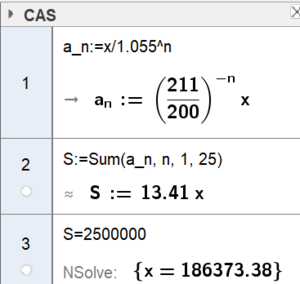
Vi setter terminbeløpet lik x og vekstfaktor lik 1,055. Vi har en geometrisk rekke der $S_{25} = 2500000$ og $ a_n = \frac{x}{1,055^n}$
Det årlige terminbeløpet blir 186 373,38 kr.
Etter 5 år vil Olivia utvide lånet for å pusse opp badet. Hun håper å få låne
500 000 kroner ekstra til samme rente, men hun vil ikke forlenge
nedbetalingstiden på lånet.
b) Hvor store blir de nye terminbeløpene?
Løsn.
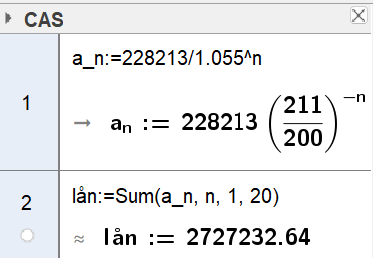
Her kan man tenke at man tar opp et nytt lån som løper parallelt med det første, så summerer man terminbeløpene. Man får en ny geometrisk rekke på 20 ledd, der $a_n= \frac{x}{1.055^n}$ og $S_{20} = 500000$. Vi setter inn i cas:
Det totale terminbeløpet blir nå 228 213,05 kr.
Olivia vet at dersom de nye terminbeløpene blir for store, må hun forlenge nedbetalingstiden.
c) Hvor lang blir nedbetalingstiden dersom hun betaler 200 000 kroner hver termin etter at hun har utvidet lånet?
Løsn.
Vi finner først ut hvor mye hun skylder banken etter det siste lånet:
Lånet er nå . Vi finner den nye løpetiden for lånet med terminbeløp på 200 000