1P 2025 Høst LK20 LØSNING: Forskjell mellom sideversjoner
| (35 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 29: | Linje 29: | ||
====a)==== | ====a)==== | ||
Grunnflaten er et kvadrat $G = s^2$ s er | Grunnflaten er et kvadrat $G = s^2$ | ||
s er sidekantene i kvadratet. | |||
| Linje 150: | Linje 152: | ||
===Oppgave 1=== | ===Oppgave 1=== | ||
====a)==== | |||
[[File:05022026-02.png|centre|600px]] | |||
$a = 0,01$ og $b= 3$ | |||
====b)==== | |||
[[File:05022026-03.png|centre|600px]] | |||
Stigningstallet er ca 210. Det betyr at vekten på fisken i gjennomsnitt øker med 210 gram, for hver centimeter den blir lengre. | |||
====c)==== | |||
[[File:05022026-04.png|centre|600px]] | |||
Den momentane veksten er ca. 290 gram når lengden er 100cm. Det betyr at dersom lengden vokser med en cm, vil vekten øke med ca 290. gram. | |||
====d)==== | |||
Dersom lengden øker med 20%: | |||
$f(1,2x) = 0,01 \dot (1,2x)^3$ | |||
$f(1,2x)= 0,01 \cdot 1,2^3 \cdot x^3 = 1,2^3 \cdot f(x) = 1,728 f(x)$ | |||
Dersom lengden øker med 20%, øker vekten med ca. 73%. | |||
===Oppgave 2=== | ===Oppgave 2=== | ||
'''Situasjon A''' | |||
Graf 1 avtar lineært, so den er det ikke. Det står mellom graf 4 og 8. Graf 8 har ikke kontakt med y aksen og faller svært raskt i starten, konsistent med omvendt proporsjonalitet. '''Graf 4 er riktig'''. | |||
''' Situasjon B''' | |||
'''Graf 8 er riktig''', argumentert for i a. | |||
'''Situasjon C''' | |||
'''Graf 2 er riktig'''. I starten av tidsforløpet øker veksten, for så å anta tilnærmet lineær vekst en periode. Veksten flater ut når det er balanse mellom fødsel og død i fuglebestanden (eventuell inn og utvandring også). | |||
'''Situasjon D''' | |||
'''Graf 3 er riktig'''. Dette er en diskontinuerlig situasjon, ingen pakker koster 74 - 134kr. å sende. Benevningen på x aksen er kg. Vi observerer at de to første pakke intervallene spenner over 5 kg, mens det siste spenner over 15 kg. Dette gjenspeiles i lengden på grafene. Vi ser også at det ikke er variasjon i pris innen ett og samme intervall, grafene er parallelle med x aksen. | |||
===Oppgave 3=== | ===Oppgave 3=== | ||
====a)==== | |||
$57 \cdot 10^9 : 229963 = 247866$ kroner per person, i gjennomsnitt | |||
====b)==== | |||
Dersom 229963 personer utgjør 4,8% av alle personer over 18 år, er det: | |||
$\frac{229963 \cdot 100}{4,8} = 4,79$ millioner personer over 18 år i Norge. | |||
===Oppgave 4=== | ===Oppgave 4=== | ||
* Hun kjøper $3 \cdot 0,454 kg = 1,36$ kg. epler | |||
*Hun betaler $ 10,16 \cdot 4,18 = 42,47$ NOK for eplene | |||
Kilopris blir $\frac {42,47 NOK}{1,36 kg} = 31,23$ NOK per kg. | |||
===Oppgave 5=== | ===Oppgave 5=== | ||
En aksje har verdi a. | |||
Verdien synker med 23% gir ny verdi 0,77a. | |||
Vi finner vekstfaktoren k som gjør at $k \cdot (0,77a)=a$, som gir: | |||
$k = \frac {a}{0,77 a} = \frac{1}{0,77}= 1,298 \approx$ 30% | |||
Aksjen må tige med 30% for å nå nivået før fallet. | |||
===Oppgave 6=== | ===Oppgave 6=== | ||
====a)==== | |||
Avstand mellom breddegrader: $1852m \cdot 60 = 111120m = 111,12$ km | |||
====b)==== | |||
Gjordens omkrets (snitt gjennom nord- og syd pol): | |||
$111,12 km \cdot 360 = 40 003$ km. Omkretsen rundt ekvator er litt større, på grunn av rotasjonen. | |||
====c)==== | |||
Forskjell i grader blir 63,4 - 59,9 = 3,5. | |||
Når en grad tilsvarer 111,12 km blir avstanden i luftlinje $3,5 \cdot 111,12 km = 389$ km. (I virkeligheten muligens litt mer) | |||
prosentandelen i forhold til jordens omkrets: | |||
$\frac{389 \cdot 100}{40003}= 0,97$% | |||
Avstanden mellom Oslo og Trondheim er nesten 1% av jordens omkrets. | |||
===Oppgave 7=== | ===Oppgave 7=== | ||
| Linje 193: | Linje 290: | ||
====c)==== | ====c)==== | ||
Areal: $A = xy + \pi \ | Areal: $A = xy + \frac 12 \cdot \pi \cdot (\frac x2)^2 = 1 \cdot 4,7 +\frac 12 \cdot \pi \cdot (\frac 12)^2 = 5,09 $ | ||
Med gitte mål blir arealet 5,09 kvadratmeter. | |||
====d)==== | ====d)==== | ||
Dersom blomsterbedet til en hver tid har en omkrets på 12 meter gir det begrensninger. Dersom vi velger x veldig liten, blir y stor og motsatt. dersom x er null har vi ikke noe bed i det hele tatt. Hvor stor kan x bli før y blir null? | |||
Frå omkretsen har vi at: | |||
$12 = 2y + x + \frac{\pi x}{2}$ | |||
$y= 6 - \frac x2 - \frac {\pi x}{4}$ | |||
Vi undersøker hva x kan være for at y er større enn null: | |||
[[File:07022026-01.png|centre|300px]] | |||
Her er '''y lik f(x)'''. | |||
Vi ser at x kan ha verdier fra 0 til 4,67 meter. Velger vi x= 4,67 meter mister vi rektangelet i bedet. Hva slags arealer vil disse lengdene gi? | |||
Vi løser omkrets lik 12, med hensyn på y. Setter inn for y i formelen for areal og får formelen i linje 1. C(x) er arealet uttrykt ved x. | |||
[[File:07022026-02.png|centre|300px]] | |||
====e)==== | |||
[[File:07022026-03.png|centre|500px]] | |||
Den grønne grafen viser gyldig område for x. Det største arealet man får er 10 kvadratmeter. Det får man ved å velge x lik 3,36 meter. | |||
Sideversjonen fra 7. feb. 2026 kl. 05:54
Del 1
Oppgave 1
4 timer og 30 minutter er det samme som 4,5 timer. Dersom gjennomsnittsfarten er 80 km/t får man
$ s = vt = 80km/t \cdot 4,5 t = 360 km $
Oppgave 2
Dersom noe koster 200 kroner med mva, kan man tenke at det er 125%
Deler man 200kr på 125, finner man en prosent. Mva:
$ mva = \frac{200kr}{125} \cdot 25 = 40 kr $
Oppgave 3
Antall støvpartikkler:
$ \frac{20}{0,000000005} = \frac{20}{5 \cdot 10^{-9}} = 4 \cdot 10^9 = 4 000 000 000 $
altså 4 milliarder støvpartikler.
Oppgave 4
a)
Grunnflaten er et kvadrat $G = s^2$
s er sidekantene i kvadratet.
h=s
Volumet blir da : $V = \frac 13 \cdot s^3$
$V = 9 dm^3$
Det gir en høyde på $h= s = \sqrt[3]{3V}= \sqrt[3]{27} = 3$
Siden volumet var i kubikk desimeter, blir høyden i pyramiden 3 dm.
b)
Dersom to størrelser er proporsjonale er den ene størrelsen lik en konstant multiplisert med den andre, feks:
V = kh
Da blir volum delt på høyde alltid samme verdi k. Slik er det ikke i denne situasjonen. Størrelsene er ikke proporsjonale.
Oppgave 5
a)
Når man leser av grafer er det lurt å finne et punkt på grafen der rutenettet krysser grafen. For grønn graf ser man at det er flere steder. for eksempel gir 10 timer 2000 kroner, altså en timelønn på 200 kr/ time. Det er litt vanskeligere å lese av den blå grafen fordi det ikke er så mange gode avlesningssteder, men vi ser at 10 timer gir 1800 kroner, noe som gir en timelønn på 180 kr/ time.
Altså tjener Nora 200kr / time og Nils 180 kr/ time.
b)
Siden de jobber like mange timer kaller vi antall timer for x
$200x = 180x + 720$ $20x = 720$ $2x =72$ $x = 36$
De jobber begge 36 timer.
Oppgave 6
a)
Månedsbilett (30 dagers) koster 1200, da kan du kjøre buss så mye du vil.
Pris per tur blir: $turpris = \frac{1200}{antallturer}$
Eller litt enklere:
$p = \frac{1200}{a}$
Innsatt i formelen over får vi:
a = 4 gir p = 300
a = 8 gir p = 150
a = 20 gir p = 60
a = 30 gir p = 40
b)
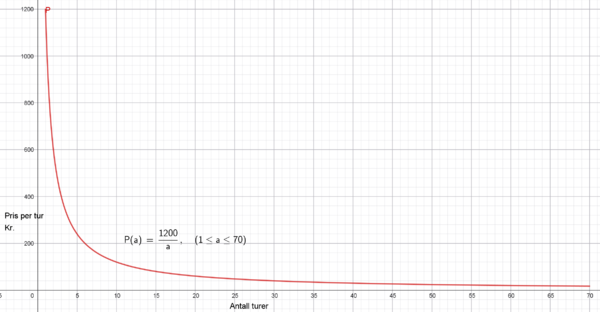
Grafen viser pris per tur i området 1 til 70 turer.
c)
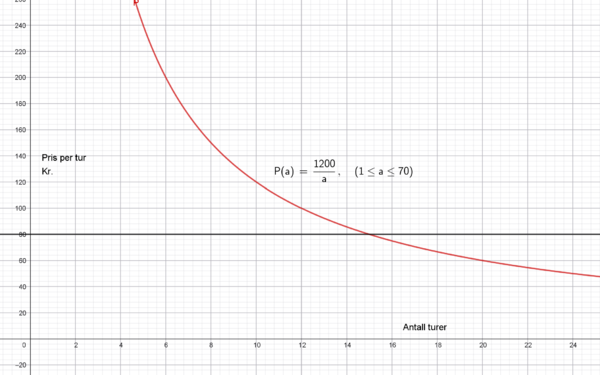
Ved 15 turer er prisen per tur den samme. Hun må reise 16 ganger eller mer for at en 30 dagers bilett skal være lønnsom.
Oppgave 7
Programmet starter med å sette verdien til "Tall" lik 1 og "differanse" lik 4. Så kommer en løkke som gjør tre ting:
- Den printer verdien av "tall"
- Den lager en ny verdi for "tall" som er summen av tall og differanse.
- Den lager en ny verdi for differansen som er summen av forrige differanse og tre.
Dette holder løkken på med til verdien av "tall" er 60 eller så nær 60 som mulig, men mindre. Det styres i programlinje 4.
første runde: print: 1, tall = 1+4=5, diff = 4+3=7
Andre runde: print: 5, tall = 5+7 =12, diff = 7+3=10
Tredje runde: print: 12, tall = 12 +10 = 22, diff = 10+3 =13
Fjerde runde: print: 22, tall = 22+13 = 35 diff = 13 + 3 = 16
Femte runde: print: 35, tall = 35 + 16 = 51, diff = 16 + 3 = 19
Sjette runde: print: 51, tall = 51 + 19 = 70, diff = 19 + 3 = 22
Her stoppes løkken av betingelsen i programlinje 4, fordi tall nå har blitt større enn 60.
De første 5-kanttallene er:
$𝑃_1=1, 𝑃_2=5, 𝑃_3=12, 𝑃_4=22, 𝑃_5=35, ....$
Differansene blir:
4, 7, 10, 13, …
Dette er en aritmetisk rekke med første ledd 4 og differanse 3.
Siri oppdaget at forskjellen mellom figur en og 2 er fire, for så å øke med tre mellom hver figur. forskjellen mellom figur 4 og 5 er for eksempel 13.
DELL 2
Oppgave 1
a)
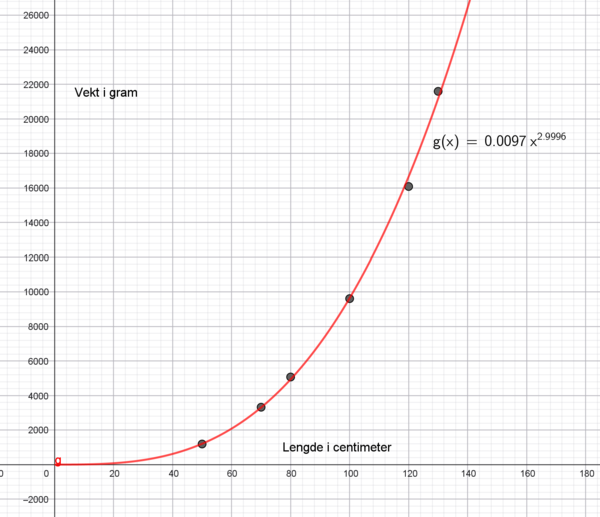
$a = 0,01$ og $b= 3$
b)
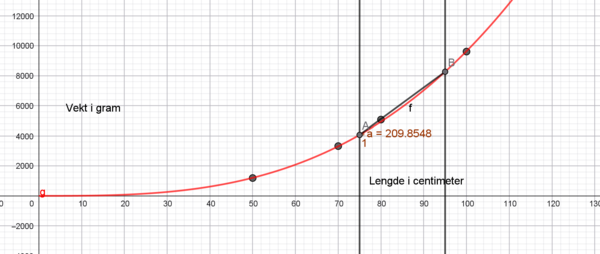
Stigningstallet er ca 210. Det betyr at vekten på fisken i gjennomsnitt øker med 210 gram, for hver centimeter den blir lengre.
c)
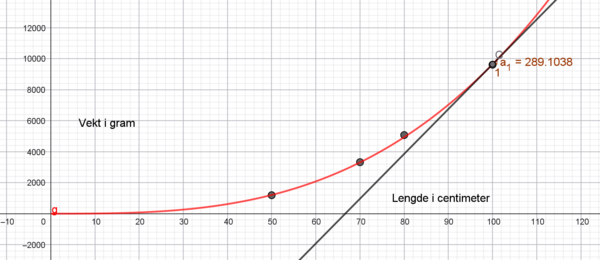
Den momentane veksten er ca. 290 gram når lengden er 100cm. Det betyr at dersom lengden vokser med en cm, vil vekten øke med ca 290. gram.
d)
Dersom lengden øker med 20%:
$f(1,2x) = 0,01 \dot (1,2x)^3$
$f(1,2x)= 0,01 \cdot 1,2^3 \cdot x^3 = 1,2^3 \cdot f(x) = 1,728 f(x)$
Dersom lengden øker med 20%, øker vekten med ca. 73%.
Oppgave 2
Situasjon A
Graf 1 avtar lineært, so den er det ikke. Det står mellom graf 4 og 8. Graf 8 har ikke kontakt med y aksen og faller svært raskt i starten, konsistent med omvendt proporsjonalitet. Graf 4 er riktig.
Situasjon B
Graf 8 er riktig, argumentert for i a.
Situasjon C
Graf 2 er riktig. I starten av tidsforløpet øker veksten, for så å anta tilnærmet lineær vekst en periode. Veksten flater ut når det er balanse mellom fødsel og død i fuglebestanden (eventuell inn og utvandring også).
Situasjon D
Graf 3 er riktig. Dette er en diskontinuerlig situasjon, ingen pakker koster 74 - 134kr. å sende. Benevningen på x aksen er kg. Vi observerer at de to første pakke intervallene spenner over 5 kg, mens det siste spenner over 15 kg. Dette gjenspeiles i lengden på grafene. Vi ser også at det ikke er variasjon i pris innen ett og samme intervall, grafene er parallelle med x aksen.
Oppgave 3
a)
$57 \cdot 10^9 : 229963 = 247866$ kroner per person, i gjennomsnitt
b)
Dersom 229963 personer utgjør 4,8% av alle personer over 18 år, er det:
$\frac{229963 \cdot 100}{4,8} = 4,79$ millioner personer over 18 år i Norge.
Oppgave 4
- Hun kjøper $3 \cdot 0,454 kg = 1,36$ kg. epler
- Hun betaler $ 10,16 \cdot 4,18 = 42,47$ NOK for eplene
Kilopris blir $\frac {42,47 NOK}{1,36 kg} = 31,23$ NOK per kg.
Oppgave 5
En aksje har verdi a.
Verdien synker med 23% gir ny verdi 0,77a.
Vi finner vekstfaktoren k som gjør at $k \cdot (0,77a)=a$, som gir:
$k = \frac {a}{0,77 a} = \frac{1}{0,77}= 1,298 \approx$ 30%
Aksjen må tige med 30% for å nå nivået før fallet.
Oppgave 6
a)
Avstand mellom breddegrader: $1852m \cdot 60 = 111120m = 111,12$ km
b)
Gjordens omkrets (snitt gjennom nord- og syd pol):
$111,12 km \cdot 360 = 40 003$ km. Omkretsen rundt ekvator er litt større, på grunn av rotasjonen.
c)
Forskjell i grader blir 63,4 - 59,9 = 3,5.
Når en grad tilsvarer 111,12 km blir avstanden i luftlinje $3,5 \cdot 111,12 km = 389$ km. (I virkeligheten muligens litt mer)
prosentandelen i forhold til jordens omkrets:
$\frac{389 \cdot 100}{40003}= 0,97$%
Avstanden mellom Oslo og Trondheim er nesten 1% av jordens omkrets.
Oppgave 7
a)
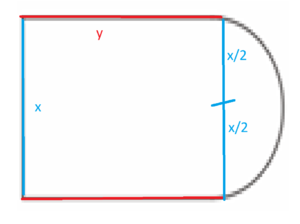
Langsidene i rektangelet kalles for y. Det er to langsider, altså 2y.
Det er en kortside i rektangelet. Den kan man kalle x.
Da er det halvsirkelen igjen. Radius er $\frac x2$. Omkretsen av en halvsirkel med denne radius blir:
$O = \frac{2 \pi \cdot r}{2} = \pi \cdot r =\frac{\pi \cdot x}{2}$
Disse tre delene utgjør den totale omkretsen.
b)
Dersom x = 1 meter.
$O = 2y + x + \frac{\pi x}{2} $
$12 = 2y + 1 + \frac{\pi}{2}$
$y= \frac{ 12-1- \frac{\pi}{2}}{2} = 4,7$ meter.
c)
Areal: $A = xy + \frac 12 \cdot \pi \cdot (\frac x2)^2 = 1 \cdot 4,7 +\frac 12 \cdot \pi \cdot (\frac 12)^2 = 5,09 $
Med gitte mål blir arealet 5,09 kvadratmeter.
d)
Dersom blomsterbedet til en hver tid har en omkrets på 12 meter gir det begrensninger. Dersom vi velger x veldig liten, blir y stor og motsatt. dersom x er null har vi ikke noe bed i det hele tatt. Hvor stor kan x bli før y blir null?
Frå omkretsen har vi at:
$12 = 2y + x + \frac{\pi x}{2}$
$y= 6 - \frac x2 - \frac {\pi x}{4}$
Vi undersøker hva x kan være for at y er større enn null:

Her er y lik f(x).
Vi ser at x kan ha verdier fra 0 til 4,67 meter. Velger vi x= 4,67 meter mister vi rektangelet i bedet. Hva slags arealer vil disse lengdene gi?
Vi løser omkrets lik 12, med hensyn på y. Setter inn for y i formelen for areal og får formelen i linje 1. C(x) er arealet uttrykt ved x.
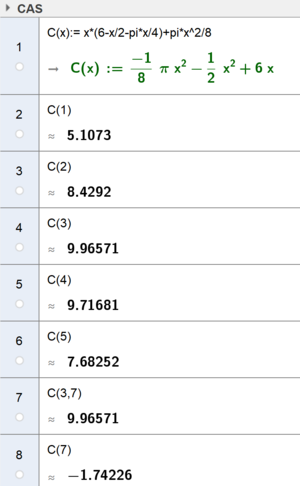
e)
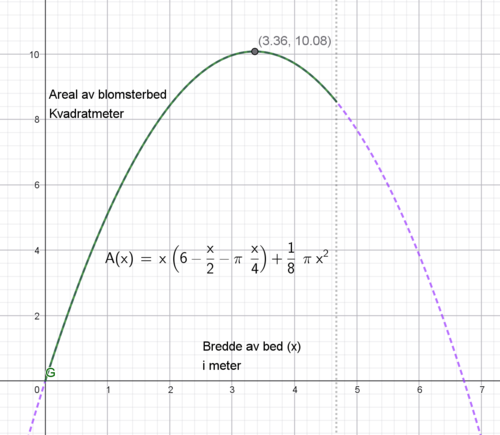
Den grønne grafen viser gyldig område for x. Det største arealet man får er 10 kvadratmeter. Det får man ved å velge x lik 3,36 meter.