1T 2014 høst LØSNING: Forskjell mellom sideversjoner
| (101 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 21: | Linje 21: | ||
==Oppgave 4== | ==Oppgave 4== | ||
$x^2+x>2 \\ x^2+x-2>0$ | |||
Løser likningen: | |||
$x^2+x-2=0 \\ x = \frac{-1\pm \sqrt{1+8}}{2} \\ x=-2 \vee x=1$ | |||
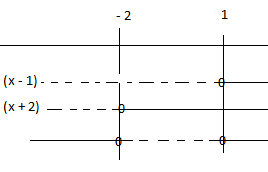
$x^2+x-2 = (x-1)(x+2)$ | |||
[[File:2014-h-1T-4-1.png]] | |||
$x \in < \leftarrow , -2> \cup <1, \rightarrow>$ | |||
==Oppgave 5== | ==Oppgave 5== | ||
| Linje 33: | Linje 46: | ||
===a)=== | ===a)=== | ||
$x \ [0] \cup [3, \rightarrow>$ | $x \in [0] \cup [3, \rightarrow>$ | ||
f er lik null for x lik 0 og 3. For x verdier større enn tre er f positiv. | f er lik null for x lik 0 og 3. For x verdier større enn tre er f positiv. | ||
| Linje 57: | Linje 70: | ||
===b)=== | ===b)=== | ||
I en | I en rettvinklet trekant er tangens definert som forholdet mellom motstående og hosliggende katet. Dersom to vinkler i trekanten er 45 grader er begge katetene like lange, og forholdet mellom dem blir en. | ||
===c)=== | ===c)=== | ||
| Linje 67: | Linje 80: | ||
Trekantene ABC og ADE er formlike. De har en felles vinkel, to felles sider og linjestykkene DE og BC er parallelle. | Trekantene ABC og ADE er formlike. De har en felles vinkel, to felles sider og linjestykkene DE og BC er parallelle. | ||
===a)=== | ===a)=== | ||
AC: $A= \frac{g \cdot h}{2} \Rightarrow 16 = \frac{AC \cdot 8}{2} \\AC = \frac{16 \cdot 2}{8} \\ AC = 4$ | |||
AD: $\frac{AD}{8} = \frac{3}{4} \\ AD = \frac{3 \cdot 8}{4} \\ AD = 6$ | |||
===b)=== | ===b)=== | ||
$BC - DE = \sqrt{8^2+4^2} - \sqrt{6^2+3^2}\\ BC - DE = \sqrt{80} -\sqrt{45} \\ BC - DE = \sqrt{16 \cdot 5} - \sqrt{9 \cdot 5} \\ BC - DE = 4 \sqrt 5 - 3 \sqrt 5 \\BC - DE = \sqrt 5$ | |||
==Oppgave 10== | ==Oppgave 10== | ||
| Linje 79: | Linje 101: | ||
$h(x)= \sqrt x = x^{ \frac 12} \\ h´(x) = \frac 12 x^{- \frac 12} = \frac{1}{2 \sqrt x}$ | $h(x)= \sqrt x = x^{ \frac 12} \\ h´(x) = \frac 12 x^{- \frac 12} = \frac{1}{2 \sqrt x}$ | ||
==DEL TO== | |||
==Oppgave 1== | |||
[[File:2014-h-1T-1-2.png]] | |||
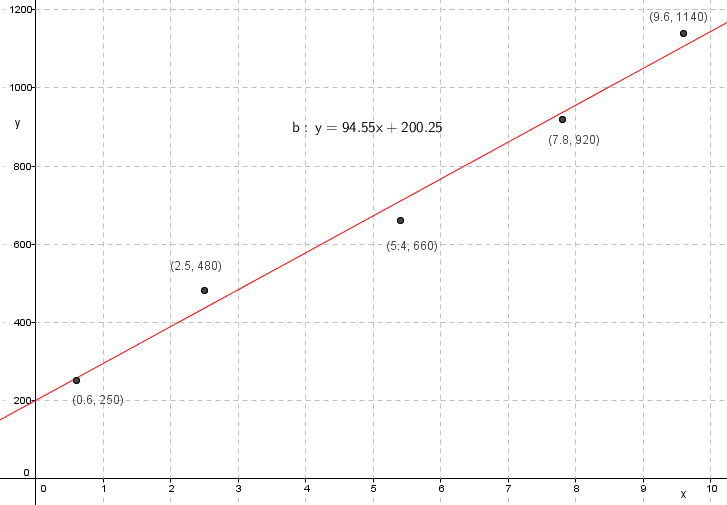
Den lineære sammenhengen er sånn ca: y = 94,56x + 200,25. | |||
==Oppgave2== | |||
===a)=== | |||
[[File:2014-h-2-2-2.png]] | |||
===b)=== | |||
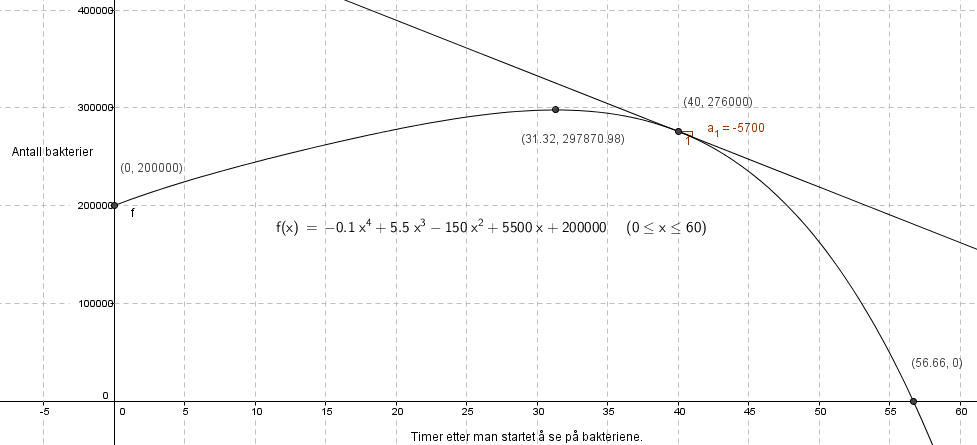
Toppunkt er (31,32 , 297870), hvilket betyr at bakteriekulturen når sitt maksimum etter ca. 31 timer, med et antall på ca. 300000. | |||
Skjæring med y-akse betyr at det er antallet bakterier ved tiden null. Dette antallet er 200000. Skjæringspunktet er (0, 200000). | |||
Grafens skjæring med x-aksen betyr at alle bakteriene er døde. Sannsynligvis matmangel, eller for mye giftstoffer. Dette skjer etter ca, 57 timer. Punktet der grafen sklærer x-aksen er (56,67, 0). | |||
===c)=== | |||
Det er svart på i delspørsmål b. | |||
===d)=== | |||
Den momentane veksten i time 40 er det samme som f `(40): | |||
$f(x)= -0,1x^4+5,5x^3-150x^2+5500x+200000 \\ f' (x)= -0,4x^3+ 16,5x^2-300x+5500 \\ f' (40) = -0,4 \cdot 40^3+16,5 \cdot 40^2 -300 \cdot 40 + 5500 \\ f'(40)= -5700$ | |||
==Oppgave 3== | |||
For å beholde oversikten er det lurt med en systematisk oversikt. Jeg velger en krysstabell: | |||
{| width="auto" | |||
| | |||
|GUTT | |||
|JENTE | |||
|Total | |||
|- | |||
|Trafikalt | |||
|8 | |||
|9 | |||
|17 | |||
|- | |||
|Ikke trafikalt | |||
|5 | |||
|8 | |||
|13 | |||
|- | |||
|Total | |||
|13 | |||
|17 | |||
|30 | |||
|} | |||
===a)=== | |||
Vi vet at eleven ikke har trafikalt grunnkurs: | |||
P(jente | ikke trafikalt grunnkurs) = $\frac {P(jente \quad og \quad ikke \quad trafikalt \quad grunnkurs)}{P(ikke \quad trafikalt \quad grunnkurs)}= \frac{8}{13}$ | |||
===b)=== | |||
Velger to. "Minst en" er da den ene, eller den andre, eller begge: | |||
P(Av to valgte har minst en trafikalt grunnkurs) = $\frac{17}{30} \cdot \frac{16}{29} + \frac{17}{30} \cdot \frac{13}{29} + \frac{13}{30} \cdot \frac{17}{29} = \frac{714}{870} \approx 0,82 = 82$ % | |||
==Oppgave 4== | |||
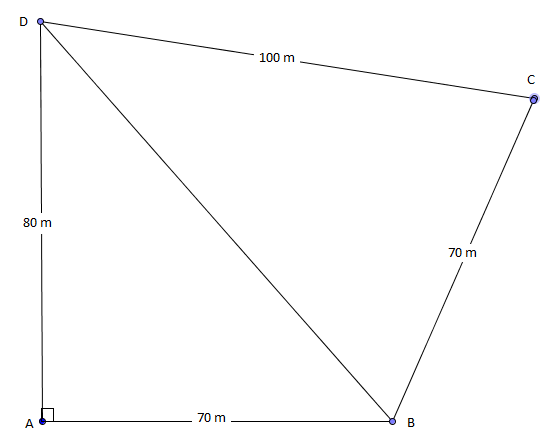
Vi trekker diagonalen BD. Lengden av denne finner vi ved å bruke pytagoras i trekanten ABD. Vi har to trekanter der alle sider er kjente. Bruker cosinussetningen til å finne en vinkel i trekanten BCD. Bruker så arealsetningen på hver av rekantene og legger disse sammen. | |||
[[File:2014-h-1T-4-2.png]] | |||
BD: $(BD)^2= (70m)^2 + (80m)^2 \\ (BD)^2 = 11300m^2 \\ BD = 106,3m$ | |||
Finner vinkel C (kunne valgt de to andre også): | |||
$106,3^2 = 100^2+ 70^2 - 2 \cdot 100 \cdot 70 \cdot cosC \\ cosC = \frac{106,3^2 - 100^2-70^2}{-2 \cdot 100 \cdot 70} \\ cosC = 0,257 \\ C = cos^{-1} (0,257)\\ C = 75,1^{\circ}$ | |||
Arealet av firkanten er summen av arealene til de to trekantene: | |||
ABD: $A= \frac {70m \cdot 80m}{2} = 2800m^2$ | |||
BCD: $A= \frac 12 \cdot 70m \cdot 100m \cdot sin 75,1 = 3382,3m^2$ | |||
Areale av firkanten ABCD blir da $2800m^2 + 3382,3 m^2 = 6182,3 m^2$ | |||
==Oppgave 5== | |||
===a)=== | |||
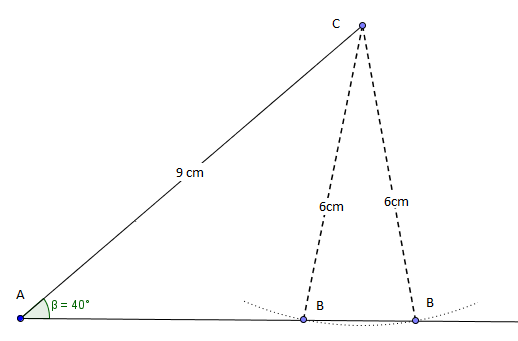
[[File:2014-h-1T-5a-2.png]] | |||
===b)=== | |||
$(BC)^2 = (AB)^2 + (AC)^2 -2 \cdot AB \cdot AC \cdot Cos A \\ (AB)^2 + 81- 18 Cos A \cdot(AB) -36 =0 \\ (AB)^2 - 13,79(AB) + 45 =0 $ | |||
Det gir AB = 5,3 cm, eller AB = 8,5cm. | |||
==Oppgave 6== | |||
===a)=== | |||
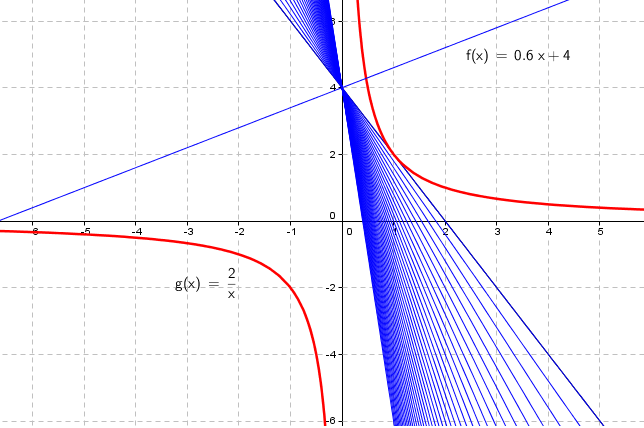
[[File:1T-2014h-6a.png]] | |||
$f(x)= ax+4$ | |||
Dersom a = -2 tangerer grafen til f grafen til g i ett punkt (1,2), dvs. en løsning. Dersom a <- 2 har likningen f(x) = g(x) ingen løsning. Dersom a > - 2 har likningen to løsninger, bortsett fra a = 0, som gir en løsning. | |||
===b)=== | |||
$ a\neq 0: \\f(x)=g(x) \\ ax+4 = \frac 2x \\ ax^2+4x-2 =0$ | |||
Bruker abc- formelen og får 16 + 8a under rottegnet. Når uttrykket er negativt har likningen ingen løsning. Når uttrykket er null har det en løsning. Når uttrykket er positivt har det to løsninger. | |||
$16+8a=0 \\ a= -2\\ a = -2 \rightarrow en\quad løsning \\ a< -2 \rightarrow ingen \quad løsning \\ a> -2 \rightarrow to \quad løsninger (a \neq 0)$ | |||
a lik null gir: | |||
$\frac 2x = 4 \\ x= \frac 12$ | |||
f er parallell med x-aksen og det er en skjæring, i punktet $( \frac 12 , 4)$ | |||
==Oppgave 7== | |||
===a)=== | |||
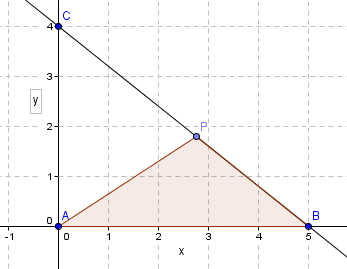
[[File:2014-h-1T-7-2.png]] | |||
Koordinatene til P er (x,y). P ligger på linjen. Linjen har konstantledd lik 4 og stigningstall $- \frac 45$, dvs. $y= - \frac 45 x +4$ som da blir y koordinaten til P. | |||
===b)=== | |||
Arealet av trekanten ABP skal være halvparten av arealet til trekanten ABC. Arealet av trekanten ABC er 10. Grunnlinjen AB er den samme, 5 i begge trekanter. Høyden i trekant ABP er y. | |||
$A= \frac{g \cdot h}{2} \\ 5 = \frac{5(- \frac45x+4)}{2} \\ 5= -2+10 \\ x= \frac 52$ | |||
som gir y = 2. $P( \frac 52 , 2) $, for at arealet av trekanten ABP skal være halvparten av ABC. | |||
Dette kan sjekkes i Geogebra, ved å dra P litt oppover, og måle arealet av skravert trekant. Slik det er tegnet har P en litt for stor x verdi, med tilhørende for liten y verdi, | |||
==Oppgave 8== | |||
Når Per er halvveis opp, har Kari tilbakelagt x trinn. Per er alltid 52 trinn høyere. | |||
$\frac y2= x+52$ | |||
y - antall trinn i tårnet. | |||
x - Karis trinn når Per er halvveis. | |||
Når Per er oppe er Karis posisjon $x+ \frac y2$. I følge Per er hun da tre ganger høyere enn hun var når Per var halvveis. | |||
$3x= x+ \frac y2$ | |||
Vi har nå to likninger med to ukjente. Det er y vi er interessert i: | |||
<math> \left[ \begin{align*}\frac y2=x+52 \\ 3x=x+ \frac y2 \end{align*}\right] </math> | |||
<math> \left[ \begin{align*} \frac y2=x+52 \\ y=4x] \end{align*}\right] </math> | |||
<math> \left[ \begin{align*} \frac{4x}{2}= x+52\\ x=52 \end{align*}\right] </math> | |||
<math> \left[ \begin{align*} y=4x= 208 \end{align*}\right] </math> | |||
Det er 208 trappetrinn i tårnet. | |||
==Oppgave 9== | |||
===a)=== | |||
Arealet av et kvadrat med sider x, er $x^2$ | |||
Arealet av et rektangel med sider x og b er xb. | |||
Siden figuren i oppgaven består av to slike figurer og har areal c må | |||
$x^2 + bx = c$ | |||
x vil da være en positiv løsning av andregradslikningen $x^2 + bx -c =0$ | |||
===b)=== | |||
Kvadratet ABCD: $(x+ \frac b2) (x+ \frac b2) = x^2 +\frac{xb}{2} + \frac{xb}{2} + \frac{b^2}{4} = x^2+ xb + \frac{b^2}{4} = c + \frac{b^2}{4}$ | |||
De to første leddene i svaret, tilsvarer c i oppgave a. Sees også fra figur tre. | |||
===c)=== | |||
x er en del av sidene $(x+ \frac b2)$ som utspenner kvadratet ABCD. Dette er en lengde, og man snakker normalt ikke om negative lengder. c er arealet av rektangelet i a. | |||
===d)=== | |||
$ (x+ \frac b2)^2 = c + \frac {b^2}{4} \\ x+ \frac b2 = \sqrt{ \frac{4c + b^2}{4}} \\ x= - \frac b2 + \frac{\sqrt{b^2+4c}}{2} \\ x = \frac{-b+ \sqrt{b^2+4c}}{2}$ | |||
Siste sideversjon per 10. mar. 2015 kl. 06:36
DEL EN
Oppgave 1
$25000000000 \cdot 0,0005 = 2,5 \cdot 10^{10} \cdot 5 \cdot 10^{-4} = 12,5 \cdot 10^6 = 1,25 \cdot 10^7$
Oppgave 2
$2^{2+ \frac x2} = 16 \\2^{2+ \frac x2} = 2^4 \\2 + \frac x2 = 4 \\ 4+x=8 \\ x=4$
Oppgave 3
$lg(2x-3)=0 \\ 10^{lg(2x-3)} = 10^0 \\ 2x-3 =1 \\ x=2$
Oppgave 4
$x^2+x>2 \\ x^2+x-2>0$
Løser likningen:
$x^2+x-2=0 \\ x = \frac{-1\pm \sqrt{1+8}}{2} \\ x=-2 \vee x=1$
$x^2+x-2 = (x-1)(x+2)$
$x \in < \leftarrow , -2> \cup <1, \rightarrow>$
Oppgave 5
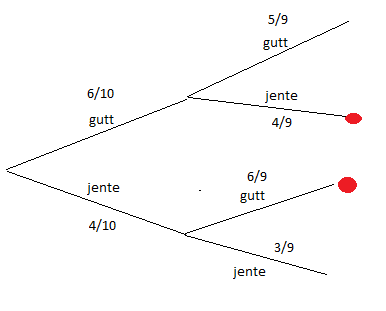
Det er to muligheter, gutt - jente og jente - gutt:
$P(en \quad av \quad hver) = \frac{6}{10} \cdot \frac{4}{9} + \frac{4}{10} \cdot \frac{6}{9} = \frac{8}{15} $
Oppgave 6
a)
$x \in [0] \cup [3, \rightarrow>$
f er lik null for x lik 0 og 3. For x verdier større enn tre er f positiv.
Den deriverte til f er negativ fra x = 0 til x = 2. f avtar i dette området.
b)
Gjennomsnittlig vekstfart:
$\frac{\Delta x}{\Delta y} = \frac{-8 -0}{2} = -4$
Oppgave 7
$\frac {3x}{x+3} - \frac {3}{x-3} - \frac {x^2-12x+9}{x^2-9} = \\ \frac{3x(x-3)}{x+3} - \frac {3(x+3)}{(x-3)(x+3)} - \frac {x^2-12x+9}{(x+3)(x-3)} =\\ \frac {3x^2-9x-3x-9-x^2+12x-9}{(x+3)(x-3)} = \\ \frac {2x^2-18}{(x+3)(x-3)} = \\ \frac {2(x+3)(x-3)}{(x+3)(x-3)} = 2$
Oppgave 8
a)
$ ( \frac 25 )^{-1} = \frac {1}{ \frac 25} = \frac 52 $ som er større enn 2.
b)
I en rettvinklet trekant er tangens definert som forholdet mellom motstående og hosliggende katet. Dersom to vinkler i trekanten er 45 grader er begge katetene like lange, og forholdet mellom dem blir en.
c)
log 100 = 2, derfor er log 200 større enn to. log 1000 = 3, så log 200 er et sted mellom 2 og 3.
Oppgave 9)
Trekantene ABC og ADE er formlike. De har en felles vinkel, to felles sider og linjestykkene DE og BC er parallelle.
a)
AC: $A= \frac{g \cdot h}{2} \Rightarrow 16 = \frac{AC \cdot 8}{2} \\AC = \frac{16 \cdot 2}{8} \\ AC = 4$
AD: $\frac{AD}{8} = \frac{3}{4} \\ AD = \frac{3 \cdot 8}{4} \\ AD = 6$
b)
$BC - DE = \sqrt{8^2+4^2} - \sqrt{6^2+3^2}\\ BC - DE = \sqrt{80} -\sqrt{45} \\ BC - DE = \sqrt{16 \cdot 5} - \sqrt{9 \cdot 5} \\ BC - DE = 4 \sqrt 5 - 3 \sqrt 5 \\BC - DE = \sqrt 5$
Oppgave 10
a)
$f´(x) = - \frac 12x^{- \frac 12 - 1} = - \frac 12 x^{- \frac 12 - \frac 22} = - \frac 12 x ^{- \frac 32} = - \frac{1}{2x^{\frac 32}} = - \frac{1}{2 \sqrt{x^3}}$
b)
$g(x) = \frac {1}{x^2} = x^{-2} \\ g´(x) = -2x^{-3} = - \frac{2}{x^3}$
$h(x)= \sqrt x = x^{ \frac 12} \\ h´(x) = \frac 12 x^{- \frac 12} = \frac{1}{2 \sqrt x}$
DEL TO
Oppgave 1
Den lineære sammenhengen er sånn ca: y = 94,56x + 200,25.
Oppgave2
a)
b)
Toppunkt er (31,32 , 297870), hvilket betyr at bakteriekulturen når sitt maksimum etter ca. 31 timer, med et antall på ca. 300000.
Skjæring med y-akse betyr at det er antallet bakterier ved tiden null. Dette antallet er 200000. Skjæringspunktet er (0, 200000).
Grafens skjæring med x-aksen betyr at alle bakteriene er døde. Sannsynligvis matmangel, eller for mye giftstoffer. Dette skjer etter ca, 57 timer. Punktet der grafen sklærer x-aksen er (56,67, 0).
c)
Det er svart på i delspørsmål b.
d)
Den momentane veksten i time 40 er det samme som f `(40):
$f(x)= -0,1x^4+5,5x^3-150x^2+5500x+200000 \\ f' (x)= -0,4x^3+ 16,5x^2-300x+5500 \\ f' (40) = -0,4 \cdot 40^3+16,5 \cdot 40^2 -300 \cdot 40 + 5500 \\ f'(40)= -5700$
Oppgave 3
For å beholde oversikten er det lurt med en systematisk oversikt. Jeg velger en krysstabell:
| GUTT | JENTE | Total | |
| Trafikalt | 8 | 9 | 17 |
| Ikke trafikalt | 5 | 8 | 13 |
| Total | 13 | 17 | 30 |
a)
Vi vet at eleven ikke har trafikalt grunnkurs:
P(jente | ikke trafikalt grunnkurs) = $\frac {P(jente \quad og \quad ikke \quad trafikalt \quad grunnkurs)}{P(ikke \quad trafikalt \quad grunnkurs)}= \frac{8}{13}$
b)
Velger to. "Minst en" er da den ene, eller den andre, eller begge:
P(Av to valgte har minst en trafikalt grunnkurs) = $\frac{17}{30} \cdot \frac{16}{29} + \frac{17}{30} \cdot \frac{13}{29} + \frac{13}{30} \cdot \frac{17}{29} = \frac{714}{870} \approx 0,82 = 82$ %
Oppgave 4
Vi trekker diagonalen BD. Lengden av denne finner vi ved å bruke pytagoras i trekanten ABD. Vi har to trekanter der alle sider er kjente. Bruker cosinussetningen til å finne en vinkel i trekanten BCD. Bruker så arealsetningen på hver av rekantene og legger disse sammen.
BD: $(BD)^2= (70m)^2 + (80m)^2 \\ (BD)^2 = 11300m^2 \\ BD = 106,3m$
Finner vinkel C (kunne valgt de to andre også):
$106,3^2 = 100^2+ 70^2 - 2 \cdot 100 \cdot 70 \cdot cosC \\ cosC = \frac{106,3^2 - 100^2-70^2}{-2 \cdot 100 \cdot 70} \\ cosC = 0,257 \\ C = cos^{-1} (0,257)\\ C = 75,1^{\circ}$
Arealet av firkanten er summen av arealene til de to trekantene:
ABD: $A= \frac {70m \cdot 80m}{2} = 2800m^2$
BCD: $A= \frac 12 \cdot 70m \cdot 100m \cdot sin 75,1 = 3382,3m^2$
Areale av firkanten ABCD blir da $2800m^2 + 3382,3 m^2 = 6182,3 m^2$
Oppgave 5
a)
b)
$(BC)^2 = (AB)^2 + (AC)^2 -2 \cdot AB \cdot AC \cdot Cos A \\ (AB)^2 + 81- 18 Cos A \cdot(AB) -36 =0 \\ (AB)^2 - 13,79(AB) + 45 =0 $
Det gir AB = 5,3 cm, eller AB = 8,5cm.
Oppgave 6
a)
$f(x)= ax+4$
Dersom a = -2 tangerer grafen til f grafen til g i ett punkt (1,2), dvs. en løsning. Dersom a <- 2 har likningen f(x) = g(x) ingen løsning. Dersom a > - 2 har likningen to løsninger, bortsett fra a = 0, som gir en løsning.
b)
$ a\neq 0: \\f(x)=g(x) \\ ax+4 = \frac 2x \\ ax^2+4x-2 =0$
Bruker abc- formelen og får 16 + 8a under rottegnet. Når uttrykket er negativt har likningen ingen løsning. Når uttrykket er null har det en løsning. Når uttrykket er positivt har det to løsninger.
$16+8a=0 \\ a= -2\\ a = -2 \rightarrow en\quad løsning \\ a< -2 \rightarrow ingen \quad løsning \\ a> -2 \rightarrow to \quad løsninger (a \neq 0)$
a lik null gir:
$\frac 2x = 4 \\ x= \frac 12$
f er parallell med x-aksen og det er en skjæring, i punktet $( \frac 12 , 4)$
Oppgave 7
a)
Koordinatene til P er (x,y). P ligger på linjen. Linjen har konstantledd lik 4 og stigningstall $- \frac 45$, dvs. $y= - \frac 45 x +4$ som da blir y koordinaten til P.
b)
Arealet av trekanten ABP skal være halvparten av arealet til trekanten ABC. Arealet av trekanten ABC er 10. Grunnlinjen AB er den samme, 5 i begge trekanter. Høyden i trekant ABP er y.
$A= \frac{g \cdot h}{2} \\ 5 = \frac{5(- \frac45x+4)}{2} \\ 5= -2+10 \\ x= \frac 52$
som gir y = 2. $P( \frac 52 , 2) $, for at arealet av trekanten ABP skal være halvparten av ABC.
Dette kan sjekkes i Geogebra, ved å dra P litt oppover, og måle arealet av skravert trekant. Slik det er tegnet har P en litt for stor x verdi, med tilhørende for liten y verdi,
Oppgave 8
Når Per er halvveis opp, har Kari tilbakelagt x trinn. Per er alltid 52 trinn høyere.
$\frac y2= x+52$
y - antall trinn i tårnet.
x - Karis trinn når Per er halvveis.
Når Per er oppe er Karis posisjon $x+ \frac y2$. I følge Per er hun da tre ganger høyere enn hun var når Per var halvveis.
$3x= x+ \frac y2$
Vi har nå to likninger med to ukjente. Det er y vi er interessert i:
<math> \left[ \begin{align*}\frac y2=x+52 \\ 3x=x+ \frac y2 \end{align*}\right] </math>
<math> \left[ \begin{align*} \frac y2=x+52 \\ y=4x] \end{align*}\right] </math>
<math> \left[ \begin{align*} \frac{4x}{2}= x+52\\ x=52 \end{align*}\right] </math>
<math> \left[ \begin{align*} y=4x= 208 \end{align*}\right] </math>
Det er 208 trappetrinn i tårnet.
Oppgave 9
a)
Arealet av et kvadrat med sider x, er $x^2$
Arealet av et rektangel med sider x og b er xb.
Siden figuren i oppgaven består av to slike figurer og har areal c må
$x^2 + bx = c$
x vil da være en positiv løsning av andregradslikningen $x^2 + bx -c =0$
b)
Kvadratet ABCD: $(x+ \frac b2) (x+ \frac b2) = x^2 +\frac{xb}{2} + \frac{xb}{2} + \frac{b^2}{4} = x^2+ xb + \frac{b^2}{4} = c + \frac{b^2}{4}$
De to første leddene i svaret, tilsvarer c i oppgave a. Sees også fra figur tre.
c)
x er en del av sidene $(x+ \frac b2)$ som utspenner kvadratet ABCD. Dette er en lengde, og man snakker normalt ikke om negative lengder. c er arealet av rektangelet i a.
d)
$ (x+ \frac b2)^2 = c + \frac {b^2}{4} \\ x+ \frac b2 = \sqrt{ \frac{4c + b^2}{4}} \\ x= - \frac b2 + \frac{\sqrt{b^2+4c}}{2} \\ x = \frac{-b+ \sqrt{b^2+4c}}{2}$