Løsning del 1 utrinn Høst 13: Forskjell mellom sideversjoner
→b): Skriveleif |
|||
| (35 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 43: | Linje 43: | ||
===b)=== | ===b)=== | ||
$-1^2-(-6+3)^2 = \\ -1-(-3)^2= \\ -1-9 = 10$ | $-1^2-(-6+3)^2 = \\ -1-(-3)^2= \\ -1-9 = -10$ | ||
==Oppgave 4== | ==Oppgave 4== | ||
| Linje 54: | Linje 54: | ||
===b)=== | ===b)=== | ||
$ \frac 94 - \frac 12 = | $ \frac 94 - \frac 12 = \frac 94 - \frac 24 = \frac 74$ | ||
===c)=== | ===c)=== | ||
$\frac 32 \cdot \frac 49 = \frac{3 \cdot 4}{ 2 \cdot 9} = \frac { | $\frac 32 \cdot \frac 49 = \frac{3 \cdot 4}{ 2 \cdot 9} = \frac{3 \cdot 2 \cdot 2}{2 \cdot 3 \cdot 3}= \frac 23$ | ||
===d)=== | ===d)=== | ||
$6: \frac 34 = \ | $6 : \frac 34 = 6 \cdot \frac 43 = \frac{6 \cdot 4}{3} = 8$ | ||
==Oppgave 5== | ==Oppgave 5== | ||
| Linje 73: | Linje 73: | ||
===b)=== | ===b)=== | ||
$\frac {2x}{3} + x = -(x-2) \\ 2x + 3x = -3(x | $\frac {2x}{3} + x = -(x-2) \quad | \cdot 3 \\ 2x + 3x = -3(x-2) \\ 5x= -3x+ 6 \\ 5x+3x= 6 \\ 8x= 6 \\ x= \frac{6}{8} \\x = \frac34$ | ||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 79: | Linje 79: | ||
x er avstanden mellom byene i centimeter, i virkeligheten. | x er avstanden mellom byene i centimeter, i virkeligheten. | ||
$ \frac 2x= \frac{1}{ | $ \frac 2x= \frac{1}{50 \: 000} \\ x= 100 \: 000 $ | ||
100 | 100 000 cm er 1000meter eller en km. Avstanden er altså 1km. | ||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 98: | Linje 98: | ||
$ \frac{1+2+2+2+2+3+4+4+6+8}{10} = \frac{34}{10} = 3,4$ | $ \frac{1+2+2+2+2+3+4+4+6+8}{10} = \frac{34}{10} = 3,4$ | ||
Median er det midterste tallet når tallene står i stigende rekkefølge, om det er to midterste tall, er medianen gjennomsnittet av disse to. Her er det tall nr. 5 og 6, altså 2 og 3. | |||
Gjennomsnittet av 2 og 3 er $\frac{2+3}{2} = 2,5$. | |||
==Oppgave 8== | ==Oppgave 8== | ||
| Linje 110: | Linje 110: | ||
==Oppgave 9== | ==Oppgave 9== | ||
0 til 9 er 10 siffer. Gjenntatt fire ganger blir det: | |||
$10 \cdot 10 \cdot 10 \cdot 10 = 10\:000$ muligheter (0000 er da også en mulighet). | |||
==Oppgave 10== | ==Oppgave 10== | ||
$-2x+1< 3 \\ -2x < 3-1 \\ -2x <2 \\ x > \frac {2}{-2} \\ x > -1$ | |||
Altså er alternativ fire det riktige. | |||
==Oppgave 11== | ==Oppgave 11== | ||
Likesidet trekant: | |||
O = 4m + 4m + 4m = 12m | |||
Sirkel med radius 2m: | |||
$O = 2\pi r = 2 \cdot 2 m \cdot \pi = 4\pi m > 12 m$ | |||
Omkretsen av sirkelen er størst. (Det spørres ikke om hvor stor omkretsen av sirkelen er, så det er ikke nødvendig å multiplisere ut) | |||
==Oppgave 12== | ==Oppgave 12== | ||
===a)=== | |||
4a - ( a+ 2a)= 4a - a - 2a = a | |||
===b)=== | |||
$\frac{a^2+a}{a}- a =\\ \frac{a(a+1)}{a} - a = \\ \frac{\not{a}(a+1)}{\not{a}}-a = \\ a+1-a = 1$ | |||
==Oppgave 13== | |||
$A= \frac{a+b}{2}h \\ 2A = (a+b)h \\ h = \frac{2A}{a+b}$ | |||
==Oppgave 14== | |||
[[File:utrinn2013-14.png]] | |||
Man ser at Pascal linjen skjærer i origo, dvs. b = 0 . Når man går fire enheter mot høyre på x- aksen går man to enheter ned på y- aksen. Stigningstallet er derfor $- \frac 12$. | |||
Likningen blir da: $y = - \frac 12x$ | |||
==Oppgave 15== | |||
Pris bjørk = x | |||
Pris gran = y | |||
\begin{bmatrix} 3x+6y=6600 \\ 4x+7y = 8200 \end{bmatrix} | |||
\begin{bmatrix} x=2200 - 2y \\ 4x+7y = 8200 \end{bmatrix} | |||
\begin{bmatrix} x=2200 - 2y \\ 4(2200 -2y)+7y = 8200 \end{bmatrix} | |||
\begin{bmatrix} x=2200 - 2y \\ 8800 -8y+7y = 8200 \end{bmatrix} | |||
\begin{bmatrix} x=2200 - 2y \\ y = 600 \end{bmatrix} | |||
\begin{bmatrix} x=1000 \\ y = 600 \end{bmatrix} | |||
En pall med bjørkeved koster 1000 kroner og en pall med granved koster 600 kroner. | |||
==Oppgave 16== | |||
Jeg bruker Geogebra for at det skal se pent ut. Du må konstruere med passer og linjal, siden dette er del en. | |||
[[File:utrinn-2013-16.png]] | |||
- Avsetter AB = 7 cm | |||
- Konstruerer 75 grader i B (midt mellom 60 og 90 grader) | |||
- Avsetter BC = 5cm | |||
- Trekker AC | |||
- Konstruerer en linje parallell med AB, gjennom C | |||
- Konstruerer en linje parallell med BC, gjennom A | |||
De to linjene krysser hverandre i D. ABCD er et parallellogram. | |||
==Oppgave 17== | |||
===a)=== | |||
Trekantprisme har halvparten så stort volum som firkantprismet: | |||
$V = \frac{6dm \cdot 6dm \cdot 8dm}{2} = 36 \cdot 4 dm^3 = 144 dm^3$ | |||
Volumet av trekantprismet er 144 kubikkdesimeter, eller 144 liter. | |||
===b)=== | |||
Finner hypotenusen i trekanten ved Pytagoras: | |||
$x = \sqrt{6^2 + 8^2} = 10$ dm | |||
Overflaten av trekantprisme blir da: | |||
$O = 36 dm^2 + 60dm^2 + 48dm^2 +2( \frac{8dm \cdot 6dm}{2}) = 192dm^2$ | |||
Overflaten av trekantprismet er 192 kvadratdesimeter. | |||
Siste sideversjon per 24. jun. 2017 kl. 12:08
DEL EN
Oppgave 1
a)
333+ 679 = 1012
b)
859 - 378 = 481
c)
$7,4 \cdot 3,6 = 26,64$
d)
24: 0,3 =
240 : 3 = 80
Oppgave 2
a)
78 dL = 7,8 L
b)
1,3 mil = 13 kilometer = 13 000 m
c)
2,5 t = 2500 kg
d)
$12 000 cm^2 = 120 dm^2 = 1,2 m^2 $
Oppgave 3
a)
$(-3 + 2^2) \cdot 3 = (-3 + 4) \cdot 3 = 1 \cdot 3 = 3$
b)
$-1^2-(-6+3)^2 = \\ -1-(-3)^2= \\ -1-9 = -10$
Oppgave 4
a)
$\frac 13 + \frac 12 = \frac 26 + \frac 36 = \frac{2+3}6 = \frac 56$
b)
$ \frac 94 - \frac 12 = \frac 94 - \frac 24 = \frac 74$
c)
$\frac 32 \cdot \frac 49 = \frac{3 \cdot 4}{ 2 \cdot 9} = \frac{3 \cdot 2 \cdot 2}{2 \cdot 3 \cdot 3}= \frac 23$
d)
$6 : \frac 34 = 6 \cdot \frac 43 = \frac{6 \cdot 4}{3} = 8$
Oppgave 5
a)
$5x+3=2x+6 \\ 5x-2x = 6-3 \\ 3x = 3 \\ x=1$
b)
$\frac {2x}{3} + x = -(x-2) \quad | \cdot 3 \\ 2x + 3x = -3(x-2) \\ 5x= -3x+ 6 \\ 5x+3x= 6 \\ 8x= 6 \\ x= \frac{6}{8} \\x = \frac34$
Oppgave 6
x er avstanden mellom byene i centimeter, i virkeligheten.
$ \frac 2x= \frac{1}{50 \: 000} \\ x= 100 \: 000 $
100 000 cm er 1000meter eller en km. Avstanden er altså 1km.
Oppgave 7
Tall:
2 , 4 , 6 , 1, 2 , 8 , 3 , 4 , 2 , 2
I stigende rekkefølge :
1, 2, 2, 2, 2, 3, 4, 4, 6, 8
Gjennomsnitt:
$ \frac{1+2+2+2+2+3+4+4+6+8}{10} = \frac{34}{10} = 3,4$
Median er det midterste tallet når tallene står i stigende rekkefølge, om det er to midterste tall, er medianen gjennomsnittet av disse to. Her er det tall nr. 5 og 6, altså 2 og 3. Gjennomsnittet av 2 og 3 er $\frac{2+3}{2} = 2,5$.
Oppgave 8
Overslag:
$1099 \approx 1100 \\ 899 \approx 900$
Buksen og genseren koster ca. 2000 kroner. 38% $\approx$ 40%, dvs. 400 kroner i avslag per tusen. Anne må betale ca 1200 kroner.
Oppgave 9
0 til 9 er 10 siffer. Gjenntatt fire ganger blir det:
$10 \cdot 10 \cdot 10 \cdot 10 = 10\:000$ muligheter (0000 er da også en mulighet).
Oppgave 10
$-2x+1< 3 \\ -2x < 3-1 \\ -2x <2 \\ x > \frac {2}{-2} \\ x > -1$
Altså er alternativ fire det riktige.
Oppgave 11
Likesidet trekant:
O = 4m + 4m + 4m = 12m
Sirkel med radius 2m:
$O = 2\pi r = 2 \cdot 2 m \cdot \pi = 4\pi m > 12 m$
Omkretsen av sirkelen er størst. (Det spørres ikke om hvor stor omkretsen av sirkelen er, så det er ikke nødvendig å multiplisere ut)
Oppgave 12
a)
4a - ( a+ 2a)= 4a - a - 2a = a
b)
$\frac{a^2+a}{a}- a =\\ \frac{a(a+1)}{a} - a = \\ \frac{\not{a}(a+1)}{\not{a}}-a = \\ a+1-a = 1$
Oppgave 13
$A= \frac{a+b}{2}h \\ 2A = (a+b)h \\ h = \frac{2A}{a+b}$
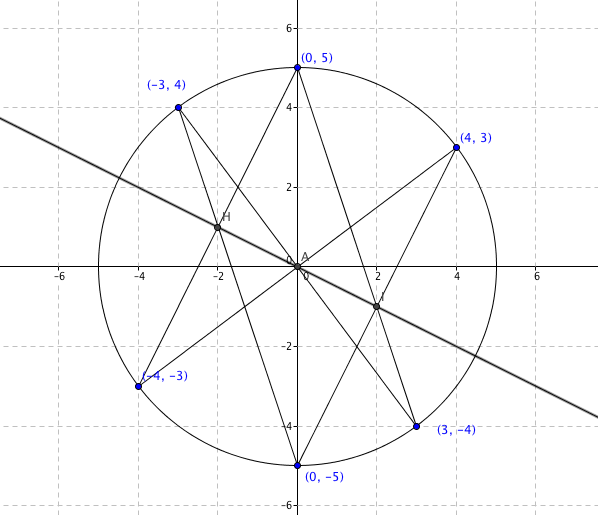
Oppgave 14
Man ser at Pascal linjen skjærer i origo, dvs. b = 0 . Når man går fire enheter mot høyre på x- aksen går man to enheter ned på y- aksen. Stigningstallet er derfor $- \frac 12$.
Likningen blir da: $y = - \frac 12x$
Oppgave 15
Pris bjørk = x
Pris gran = y
\begin{bmatrix} 3x+6y=6600 \\ 4x+7y = 8200 \end{bmatrix}
\begin{bmatrix} x=2200 - 2y \\ 4x+7y = 8200 \end{bmatrix}
\begin{bmatrix} x=2200 - 2y \\ 4(2200 -2y)+7y = 8200 \end{bmatrix}
\begin{bmatrix} x=2200 - 2y \\ 8800 -8y+7y = 8200 \end{bmatrix}
\begin{bmatrix} x=2200 - 2y \\ y = 600 \end{bmatrix}
\begin{bmatrix} x=1000 \\ y = 600 \end{bmatrix}
En pall med bjørkeved koster 1000 kroner og en pall med granved koster 600 kroner.
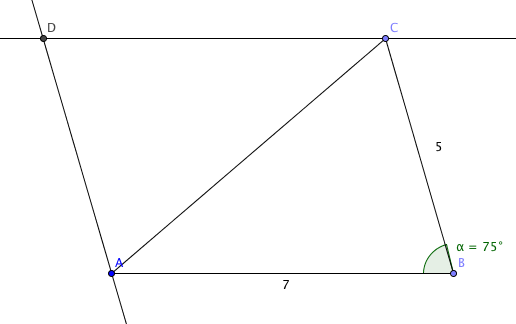
Oppgave 16
Jeg bruker Geogebra for at det skal se pent ut. Du må konstruere med passer og linjal, siden dette er del en.
- Avsetter AB = 7 cm
- Konstruerer 75 grader i B (midt mellom 60 og 90 grader)
- Avsetter BC = 5cm
- Trekker AC
- Konstruerer en linje parallell med AB, gjennom C
- Konstruerer en linje parallell med BC, gjennom A
De to linjene krysser hverandre i D. ABCD er et parallellogram.
Oppgave 17
a)
Trekantprisme har halvparten så stort volum som firkantprismet:
$V = \frac{6dm \cdot 6dm \cdot 8dm}{2} = 36 \cdot 4 dm^3 = 144 dm^3$
Volumet av trekantprismet er 144 kubikkdesimeter, eller 144 liter.
b)
Finner hypotenusen i trekanten ved Pytagoras:
$x = \sqrt{6^2 + 8^2} = 10$ dm
Overflaten av trekantprisme blir da:
$O = 36 dm^2 + 60dm^2 + 48dm^2 +2( \frac{8dm \cdot 6dm}{2}) = 192dm^2$
Overflaten av trekantprismet er 192 kvadratdesimeter.