Løsning del 2 utrinn Vår 15 eksempeloppgave: Forskjell mellom sideversjoner
→c): Svarte på spørsmålet |
|||
| (60 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 8: | Linje 8: | ||
*[https://sites.google.com/a/marienlystskole.org/marienlystmatte/eksamenssett/del-1/del-2 Løsning av alle oppgaver som videoer] | *[https://sites.google.com/a/marienlystskole.org/marienlystmatte/eksamenssett/del-1/del-2 Løsning av alle oppgaver som videoer] | ||
==Oppgave 1 == | |||
===a)=== | |||
[[File:mat0010-e-15-1b.png]] | |||
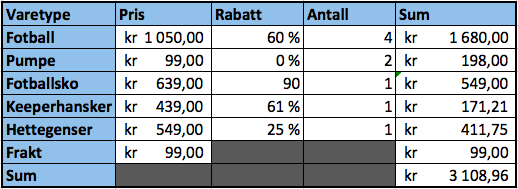
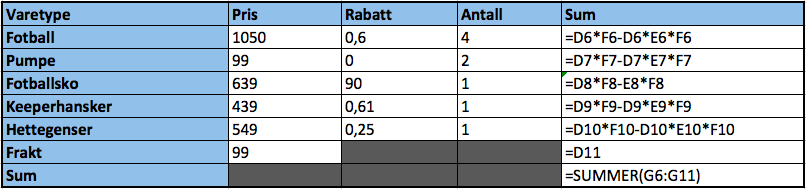
Hun må betale kr. 3108,96. | |||
[[File:mat0010-e-15-1b_ny.png]] | |||
===b)=== | |||
[[File:mat0010-e-15-1b2.png]] | |||
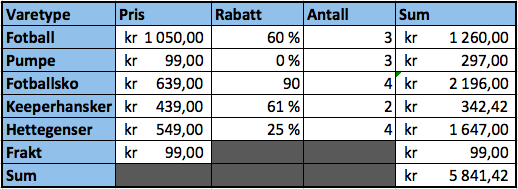
Hun må betale 5841,42 kroner. | |||
==Oppgave 2== | |||
===a)=== | |||
[[File:mat0010-e-15-1b3.png]] | |||
===b)=== | |||
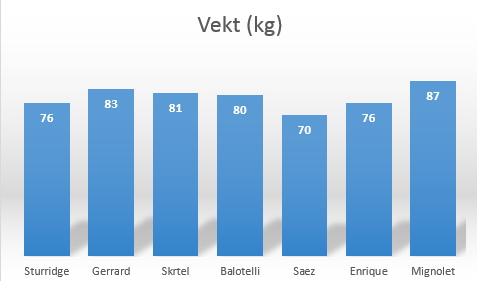
Et linjediagram indikerer kontinuitet over tid, mellom målepunkter. Det er ingen sammenheng mellom spillernes masse (vekt) over tid, eller på andre måter. | |||
==Oppgave 3== | |||
===a)=== | |||
$4 \cdot 4 \cdot 3 \cdot 3 = 144$ kombinasjoner. | |||
===b)=== | |||
Vi forutsetter at skjorte 1 og 2 er identisk med skjorte 2 og 1. | |||
Om du trekker skjorte 1 kan du i tillegg trekke 2, 3 eller 4, altså 3 muligheter (1,2),(1,3),(1,4). | |||
Om du trekker skjorte 2 kan du i tillegg trekke 3 eller 4, altså to muligheter (2,3), (2,4) | |||
Om du trekker skjorte 3 kan du også trekke 4, altså en mulighet (3,4) | |||
Det blir tilsammen seks kombinasjoner. | |||
Litt mere matematisk kan det skrives slik: | |||
$4C2 = \frac{4!}{(2!(4-2)!} = 3\cdot 2 \cdot 1 = 6$ | |||
==Oppgave 4== | |||
===a)=== | |||
$V(r)= \frac 43 \pi r^3 $ | |||
$r = \frac{O}{2\pi} \approx 10,66 cm$ | |||
$V(10,66 cm) = \frac43 \cdot \pi \cdot (10,66 cm)^3 \\ V(10,66cm) = 5074 cm^3$ | |||
5000 kubikkcentimeter tilsvarer 5 liter. | |||
===b)=== | |||
Overflate av kule: $ O(r) = 4 \pi r^2 \\ O(10,66 cm)= 4 \cdot \pi \cdot (10,66 cm)^2 \\O(10,66 cm) = 1428 cm^2 $ | |||
===c)=== | |||
$r=\sqrt{ \frac {O}{4 \pi}} = \sqrt{\frac{1000cm^2}{4 \pi}} \approx 8,92 cm $ | |||
Volum: | |||
$V(8,92)= \frac 43 \pi (8,92 cm)^3 = 2973 cm^3$ | |||
Volumet ligger på ca. 3 liter, så da er vel dette en 3er fotball. | |||
==Oppgave 5== | |||
===a)=== | |||
En drikk som er blandet i forholdet 1:2 består av 3 deler. Det er $\frac 13 \cdot 2 liter = \frac 23$ liter næringsstoff og $\frac 43$ liter vann, i en blanding på 2 liter.. | |||
===b)=== | |||
Dersom 2 deler vann er $\frac 43$ er en del vann $\frac 23$. Dvs. det må tilsettes to tredje dels liter for at forholdet skal bli 1:3. | |||
==Oppgave 6== | |||
===a)=== | |||
Trekant ABC er en 30, 60, 90 graders trekant. Da er hypotenusen dobbelt så lang som korteste katet, altså 16 meter. | |||
===b)=== | |||
Bruker Pytagoras | |||
$AB = \sqrt{(16m)^2-(8m)^2} \approx 13,85 m$ | |||
===c)=== | |||
Finner AD med Pytagoras på trekant ABD | |||
$AD = \sqrt{(13,85m)^2+(15,32m)^2} = 20,65m$ | |||
Finner AE med Pytagoras på trekant ADE | |||
$AE = \sqrt{(20,65m)^2+(2,44m)^2} = 20,79m$ | |||
Gjennomsnittsfart fra A til E | |||
$v = \frac st = \frac{20,79m}{0,8m} = 26 m/s$ | |||
==Oppgave 7== | ==Oppgave 7== | ||
[https://www.youtube.com/watch?v=M7rwVKCY11U Løsning på denne oppgaven som video laget av Mette Bendiksen] | [https://www.youtube.com/watch?v=M7rwVKCY11U Løsning på denne oppgaven som video laget av Mette Bendiksen] | ||
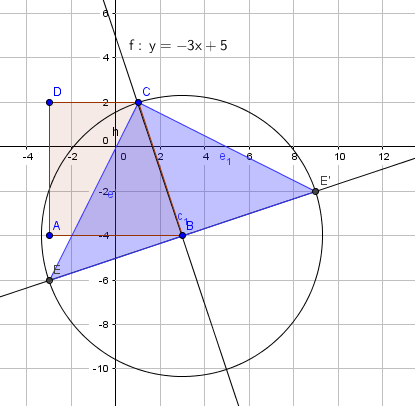
[[File:mat0010-e-15-7abc.png]] | |||
===a)=== | |||
Det er et trapes. | |||
===b)=== | |||
Se figur over. | |||
===c)=== | |||
Ser fra figuren over at punktene ( -3, -6) og ( 9, -2) tilfredsstiller kravene til E. | |||
==Oppgave 8== | |||
De svømmer I et 25 meters basseng. Kine er presis i starten og vender først, etter ca 18 sekunder. Mina vender etter ca 25 sekunder og har de siste 10 meterne tapt mye i forhold til Kine. Kine svømmer bra til det er ca 17 meter igjen, da sprekker hun og blir forbisvømt av Mina etter 30 sekunder, 15 meter før mål. Mina kommer i mål etter ca. 46 sekunder og Kine etter ca. 56. | |||
==Oppgave 9== | ==Oppgave 9== | ||
| Linje 20: | Linje 153: | ||
===a)=== | ===a)=== | ||
Marius (x): "Gi meg 10 klinkekuler, så har vi like mange" gir oss: x +10 = y - 10 som er lik x - y = -20. | |||
Kathrine (y): "Hvis du i stedet gir meg 10 klinkekuler, så vil jeg ha dobbelt så mange som deg" gir oss: | |||
$2(x - 10) = y+ 10 \\ x - 20 = y + 10 \\ 2x -y = 30$ | |||
===b)=== | ===b)=== | ||
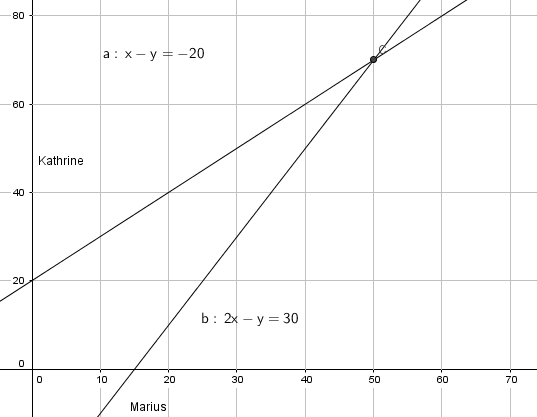
[[File:u2015-9-eks.png]] | [[File:u2015-9-eks.png]] | ||
Vi ser at Marius har 50 kuler og Kathrine har 70. | |||
===c)=== | ===c)=== | ||
\begin{bmatrix} x-y = -20 \\ 2x-y=30 \end{bmatrix} | |||
\begin{bmatrix} -x+y=20 \\ 2x-y = 30 \end{bmatrix} | |||
\begin{bmatrix} 2x-x=20+30 \end{bmatrix} | |||
\begin{bmatrix} x = 50 \end{bmatrix} | |||
Innsatt for x = 50 gir det 50 - y = -20, dvs y = 70 | |||
$x=50 \wedge y=70$ | |||
Marius har 50 kuler og Kathrine har 70. | |||
==Oppgave 10== | ==Oppgave 10== | ||
[https://www.youtube.com/watch?v=VMaueRN6zlw Løsning på denne oppgaven som video laget av Mette Bendiksen] | [https://www.youtube.com/watch?v=VMaueRN6zlw Løsning på denne oppgaven som video laget av Mette Bendiksen] | ||
===a)=== | |||
Område 1: $20m \cdot 50m = 1000m^2$ | |||
Område 2: $60m \cdot 10m = 600m^2$ | |||
===b)=== | |||
Dersom to av sidene er x er lengden som er igjen til de to andre sidene lik 140- 2x. Når man deler på 2 finner man at en av disse sidene må være 70-x. | |||
$A(x)= x(70 - x) = -x^2 +70x$ | |||
x kan ligge mellom 0 og 70 meter. | |||
$x \in [0, 70]$ | |||
===c)=== | |||
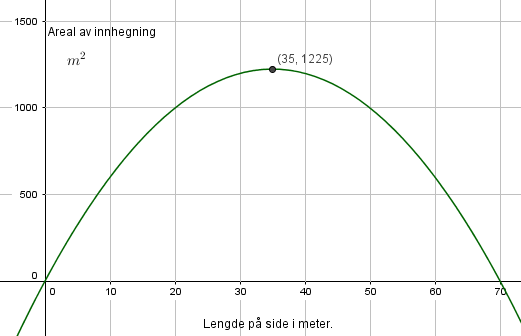
[[File:u2015-10-eks.png]] | |||
x = 35 gir størst areal. Siden den andre siden er 70-x, ser vi at den også blir 35 m. Det største området er altså et kvadrat. | |||
Siste sideversjon per 22. jun. 2017 kl. 18:50
- Oppgaven Del 1 som pdf
- Løsning del 1
- Oppgaven Del 2 som pdf
- Løsning på oppgaven som pdf
- Løsning på oppgaven på doc-format
- Løsning på oppgave 4, 7, 9 og 10 løst med ggb cas og grafikk som pdf
- Løsning av alle oppgaver som videoer
Oppgave 1
a)
Hun må betale kr. 3108,96.
b)
Hun må betale 5841,42 kroner.
Oppgave 2
a)
b)
Et linjediagram indikerer kontinuitet over tid, mellom målepunkter. Det er ingen sammenheng mellom spillernes masse (vekt) over tid, eller på andre måter.
Oppgave 3
a)
$4 \cdot 4 \cdot 3 \cdot 3 = 144$ kombinasjoner.
b)
Vi forutsetter at skjorte 1 og 2 er identisk med skjorte 2 og 1.
Om du trekker skjorte 1 kan du i tillegg trekke 2, 3 eller 4, altså 3 muligheter (1,2),(1,3),(1,4).
Om du trekker skjorte 2 kan du i tillegg trekke 3 eller 4, altså to muligheter (2,3), (2,4)
Om du trekker skjorte 3 kan du også trekke 4, altså en mulighet (3,4)
Det blir tilsammen seks kombinasjoner.
Litt mere matematisk kan det skrives slik:
$4C2 = \frac{4!}{(2!(4-2)!} = 3\cdot 2 \cdot 1 = 6$
Oppgave 4
a)
$V(r)= \frac 43 \pi r^3 $
$r = \frac{O}{2\pi} \approx 10,66 cm$
$V(10,66 cm) = \frac43 \cdot \pi \cdot (10,66 cm)^3 \\ V(10,66cm) = 5074 cm^3$
5000 kubikkcentimeter tilsvarer 5 liter.
b)
Overflate av kule: $ O(r) = 4 \pi r^2 \\ O(10,66 cm)= 4 \cdot \pi \cdot (10,66 cm)^2 \\O(10,66 cm) = 1428 cm^2 $
c)
$r=\sqrt{ \frac {O}{4 \pi}} = \sqrt{\frac{1000cm^2}{4 \pi}} \approx 8,92 cm $
Volum:
$V(8,92)= \frac 43 \pi (8,92 cm)^3 = 2973 cm^3$
Volumet ligger på ca. 3 liter, så da er vel dette en 3er fotball.
Oppgave 5
a)
En drikk som er blandet i forholdet 1:2 består av 3 deler. Det er $\frac 13 \cdot 2 liter = \frac 23$ liter næringsstoff og $\frac 43$ liter vann, i en blanding på 2 liter..
b)
Dersom 2 deler vann er $\frac 43$ er en del vann $\frac 23$. Dvs. det må tilsettes to tredje dels liter for at forholdet skal bli 1:3.
Oppgave 6
a)
Trekant ABC er en 30, 60, 90 graders trekant. Da er hypotenusen dobbelt så lang som korteste katet, altså 16 meter.
b)
Bruker Pytagoras
$AB = \sqrt{(16m)^2-(8m)^2} \approx 13,85 m$
c)
Finner AD med Pytagoras på trekant ABD
$AD = \sqrt{(13,85m)^2+(15,32m)^2} = 20,65m$
Finner AE med Pytagoras på trekant ADE
$AE = \sqrt{(20,65m)^2+(2,44m)^2} = 20,79m$
Gjennomsnittsfart fra A til E
$v = \frac st = \frac{20,79m}{0,8m} = 26 m/s$
Oppgave 7
Løsning på denne oppgaven som video laget av Mette Bendiksen
a)
Det er et trapes.
b)
Se figur over.
c)
Ser fra figuren over at punktene ( -3, -6) og ( 9, -2) tilfredsstiller kravene til E.
Oppgave 8
De svømmer I et 25 meters basseng. Kine er presis i starten og vender først, etter ca 18 sekunder. Mina vender etter ca 25 sekunder og har de siste 10 meterne tapt mye i forhold til Kine. Kine svømmer bra til det er ca 17 meter igjen, da sprekker hun og blir forbisvømt av Mina etter 30 sekunder, 15 meter før mål. Mina kommer i mål etter ca. 46 sekunder og Kine etter ca. 56.
Oppgave 9
Løsning på denne oppgaven som video laget av Mette Bendiksen
a)
Marius (x): "Gi meg 10 klinkekuler, så har vi like mange" gir oss: x +10 = y - 10 som er lik x - y = -20.
Kathrine (y): "Hvis du i stedet gir meg 10 klinkekuler, så vil jeg ha dobbelt så mange som deg" gir oss:
$2(x - 10) = y+ 10 \\ x - 20 = y + 10 \\ 2x -y = 30$
b)
Vi ser at Marius har 50 kuler og Kathrine har 70.
c)
\begin{bmatrix} x-y = -20 \\ 2x-y=30 \end{bmatrix} \begin{bmatrix} -x+y=20 \\ 2x-y = 30 \end{bmatrix} \begin{bmatrix} 2x-x=20+30 \end{bmatrix}
\begin{bmatrix} x = 50 \end{bmatrix}
Innsatt for x = 50 gir det 50 - y = -20, dvs y = 70
$x=50 \wedge y=70$
Marius har 50 kuler og Kathrine har 70.
Oppgave 10
Løsning på denne oppgaven som video laget av Mette Bendiksen
a)
Område 1: $20m \cdot 50m = 1000m^2$
Område 2: $60m \cdot 10m = 600m^2$
b)
Dersom to av sidene er x er lengden som er igjen til de to andre sidene lik 140- 2x. Når man deler på 2 finner man at en av disse sidene må være 70-x.
$A(x)= x(70 - x) = -x^2 +70x$
x kan ligge mellom 0 og 70 meter. $x \in [0, 70]$
c)
x = 35 gir størst areal. Siden den andre siden er 70-x, ser vi at den også blir 35 m. Det største området er altså et kvadrat.