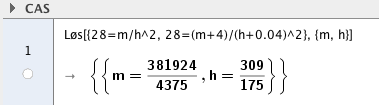S1 2015 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (42 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://ndla.no/nb/node/157692?fag=57934 alternativ løsning fra NDLA] | |||
==DEL EN== | ==DEL EN== | ||
| Linje 130: | Linje 132: | ||
Colaflasken kan velges som nr 1, 2 eller 3: | Colaflasken kan velges som nr 1, 2 eller 3: | ||
$P(cola)= \frac{1}{5}$ | $P(cola)= \frac{1}{5} \cdot 1 \cdot 1 + \frac45 \cdot \frac14 \cdot 1 + \frac 45 \cdot \frac 34 \cdot \frac 13 = \frac 35 = 60$% | ||
==Oppgave 8== | ==Oppgave 8== | ||
| Linje 136: | Linje 138: | ||
===a)=== | ===a)=== | ||
x er dekar gulerøtter og y dekar poteter. | |||
$x \geq 0 \quad$ Dersom man skal dyrke gulerøtter trenger man areal. | |||
$y \geq 0 \quad$ Det samme gjelder for poteter. | |||
$x+y \leq 15 \quad$ Det totale området er 15 dekar. Summen av gulerot og potet areale må være mindre eller lik 15. | |||
$5x +2,5y \leq 50 \\ 2x +y \leq 20 \quad$ | |||
Han har maksimum 50 timer å bruke på klargjøring. Det tar dobbelt så lang tid å klargjøre en dekar for gulerøtter, i forhold til poteter. | |||
===b)=== | ===b)=== | ||
[[File:s1-h2015-8b.png]] | |||
===c)=== | ===c)=== | ||
Fra Figuren i b ser man at han bør bruke 5 dekar på gulerøtter, og 10 dekar på poteter, Inntekten blir da 60 000 + 80 000, altså 140 000 kroner. | |||
Laget først en tilfeldig nivålinje basert på 1200x +8000y. Denne ble så parallellforskjøvet til den ytterste begrensningen gitt av ulikhetene. Linjen går da gjennom punktet (5, 10) som er det optimale produksjonsforholdet under de gitte betingelser. | |||
==Oppgave 9== | ==Oppgave 9== | ||
$4^x-6\cdot 2^x+8 =0 \\ (2^x)^2-6 \cdot 2^x+8=0 \\ u = 2^x \\ u^2 -6u + 8=0 \\ u= \frac{6 \pm \sqrt{36-32}}{2}$ | $4^x-6\cdot 2^x+8 =0 \\ (2^x)^2-6 \cdot 2^x+8=0 \\ u = 2^x \\ u^2 -6u + 8=0 \\ u= \frac{6 \pm \sqrt{36-32}}{2} \\ u=2 \vee u = 4 \\ 2^x=2 \vee 2^x= 8 \\ 2^x=2 \vee 2^x= 2^3 \\ x=1 \vee x=3 $ | ||
==DEL TO== | ==DEL TO== | ||
| Linje 150: | Linje 168: | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | ===a)=== | ||
[[File:s1-h2015-21a.png]] | |||
Sannsynligheten for tre jenter og tre gutter blir trukket er 30,8%. | |||
===b)=== | ===b)=== | ||
Sannsynlighet for at begge kjønn er representert er: | |||
P (begge kjønn) = 1 - P( bare gutter )- P(bare jenter) = 1 - 0,0012 - 0,0283 = 0,9706 | |||
[[File:s1-h2015-21b.png]] | |||
Altså ca. 97% | |||
===c)=== | ===c)=== | ||
Vi har tre forskjellige grupper, "Geir", "gutter minus Geir" og "jenter". Geir skal være med, to tilfeldige gutter skal være med, og tre tilfeldige jenter skal være med: | |||
P( Geir er med blant tre jenter og tre gutter)=$ \frac{\binom{1}{1} \binom{9}{2} \binom{15}{3}}{\binom{25}{6}} = 0,0925$ | |||
Det er ca. 9,25% sannsynlig at Geir blir med under gitte betingelser. | |||
==Oppgave 2== | ==Oppgave 2== | ||
===a)=== | ===a)=== | ||
$BMI= \frac{m}{h^2} = \frac{78}{1,77^2} = 24,9$ | |||
===b)=== | ===b)=== | ||
$BMI= \frac{m}{h^2} \\ h= \sqrt{\frac{85}{28}} = 1,74$ | |||
Personen er 174 cm høy. | |||
===c)=== | ===c)=== | ||
Terje: masse = m, høyde =h | |||
Svein: masse = (m+4), høyde = (h + 0,04) | |||
Begge med en BMI på 28: | |||
$28 = \frac{m}{b^2} \quad \wedge \quad 28 = \frac{(m+4)}{(h+ 0,04)^2}$ | |||
I CAS: | |||
[[File:s1-h2015-22c.png]] | |||
Terje er 1,77 meter høy, med en masse på 87,3 kilogram. Svein har en masse på 91,3 kilogram og en høyde på 1,81 meter. | |||
==Oppgave 3== | ==Oppgave 3== | ||
===a)=== | ===a)=== | ||
[[File:s1-h2015-4abcd.png]] | |||
Den prosentvise veksten blir 4,6, i følge modellen. | |||
===b)=== | ===b)=== | ||
Lønnen i 2015 blir ca 46 500 kr, i følge modellen. | |||
===c)=== | ===c)=== | ||
Se funksjon f i figuren i a. | |||
===d)=== | ===d)=== | ||
Funksjon d viser forskjellen mellom de to modellene. I 2012 vil forskjellen være ca. 10 000 kr. | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | ===a)=== | ||
Areal: | |||
$A= x \cdot f(x) = x \cdot \frac{5}{x^2+2} = \frac{5x}{x^2+2}$ | |||
===b)=== | ===b)=== | ||
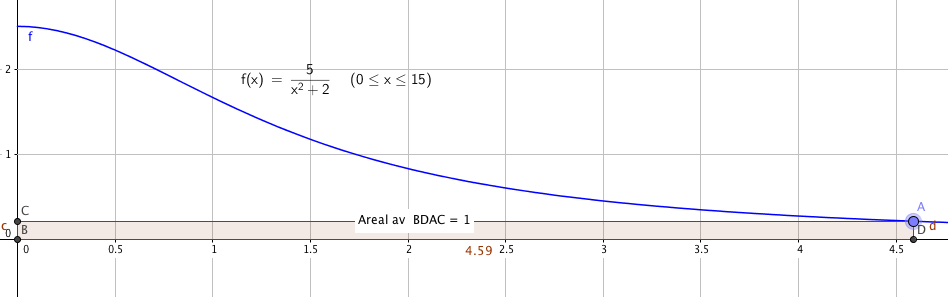
Tegner grafen i Geogebra og legger et glidende punkt på den. Ser da at det er to x verdier som gir oss areal lik en: | |||
[[File:s1-h2015-4a1.png]] | |||
[[File:s1-h2015-4a2.png]] | |||
x= 0,44 og x= 4,59 gir rektangelet arealet lik 1. | |||
===c)=== | ===c)=== | ||
[[File:s1-h2015-24c.png]] | |||
Arealet blir størst når x er lik kvadratroten av to. Da er arealet $\frac{5 \cdot \sqrt{2}}{4}$. | |||
Siste sideversjon per 15. feb. 2016 kl. 14:18
DEL EN
Oppgave 1
a)
$2x^2-3x=0 \\x(2x-3)= 0 \\ x=0 \vee x = \frac 32$
b)
$2^{3x+1} = 4^{17} \\ 2^{3x+1} = 2^{34} \\ 3x+1 = 34 \\ x = 11$
c)
$lg(2x+2) = 3 + lg2 \\ lg(2x+2) = lg(1000\cdot 2) \\ 2x= 1998 \\ x= 999$
Oppgave 2
a)
$\frac{8a^3(a^{-1}b)^2}{(2ab)^2}= \\ \frac{2^3a^3a^{-2}b^2}{2^2a^2b^2} = \\ 2^{3-2}a^{3-2-2}b^{2-2} = \\ 2a^{-1} = \\ \frac2a$
b)
$(x+y)(x-y) + (y+x) (y-x) - (x+y)(x-y)= \\ y^2-x^2$
Oppgave 3
<math> \left[ \begin{align*} 2x^2+x+y=7\\ 3x+y=-5 \end{align*}\right] </math>
<math> \left[ \begin{align*} 2x^2+x+y=7\\ y=-5 -3x \end{align*}\right] </math>
<math> \left[ \begin{align*} 2x^2+x+(-5-3x)=7\\ y=-5 - 3x \end{align*}\right] </math>
Løser første likning og får to x verdier:
$2x^2-2x- 12 =0 \\ x= \frac{2 \pm \sqrt{4+96}}{4} \\ x=-2 \vee x= 3$
Det gir følgende y verdier:
x =-2: y= - 5+6 =1
x = 3: y = - 14
Løsning; $(-2,1) \wedge (3, -14)$
Oppgave 4
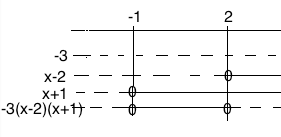
$-3(x-2)(x+1)<0$
Fortegnsskjema:
$x \in < \leftarrow, -1 > \cup <2, \rightarrow>$
Oppgave 5
a)
$f(x)=x^3-x^2-x+3 \\ f(0)= 3 \\ f(2)= 8-4-2+3= 5$
Gjennomsnittlig vekstfart i intervallet blir da $\frac{f(2)-f(0)}{2} = 1$
b)
$f´(x) =3x^2-2x-1 \\ f´(0) = -1$
Siden den deriverte er negativ for x = 0, synker grafen til f.
c)
$f´(x)=0 \\ 3x^2-2x-1=0 \\ x= \frac{2 \pm \sqrt{4+12}}{6} \\ x= 1 \vee x= - \frac 13$
Fra b har vi at grafen synker for x = 0
X=1 gir da et minimum og x= $-\frac13$ gir maksimum.
$f(1) =1 -1 -1 +3= 2\\ f(-\frac 13)= 3,19$
Oppgave 6
a)
Skjæring med y akse:
$g(0) = -3$
Skjæring med y aksen er i -3, altså (0, -3).
Skjæring med x akse:
$g(x)= 0 \\ 2x-3 = 0 \\ x= \frac 32$,
altså $(\frac32,0)$
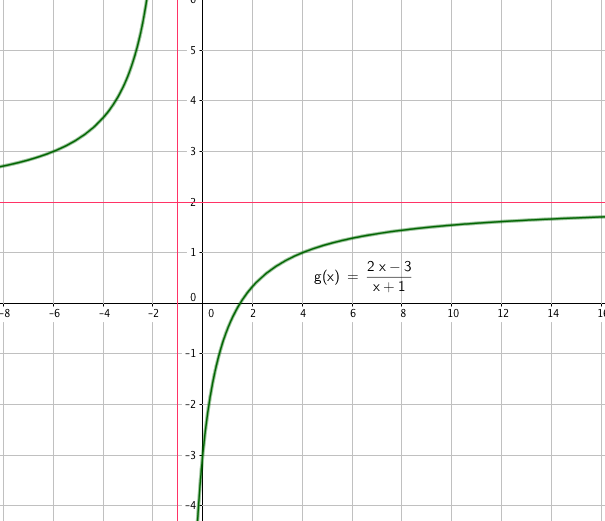
b)
Oppgave 7
a)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
b)
Fra a gir det 10 mulige kombinasjoner.
c)
Colaflasken kan velges som nr 1, 2 eller 3:
$P(cola)= \frac{1}{5} \cdot 1 \cdot 1 + \frac45 \cdot \frac14 \cdot 1 + \frac 45 \cdot \frac 34 \cdot \frac 13 = \frac 35 = 60$%
Oppgave 8
a)
x er dekar gulerøtter og y dekar poteter.
$x \geq 0 \quad$ Dersom man skal dyrke gulerøtter trenger man areal.
$y \geq 0 \quad$ Det samme gjelder for poteter.
$x+y \leq 15 \quad$ Det totale området er 15 dekar. Summen av gulerot og potet areale må være mindre eller lik 15.
$5x +2,5y \leq 50 \\ 2x +y \leq 20 \quad$
Han har maksimum 50 timer å bruke på klargjøring. Det tar dobbelt så lang tid å klargjøre en dekar for gulerøtter, i forhold til poteter.
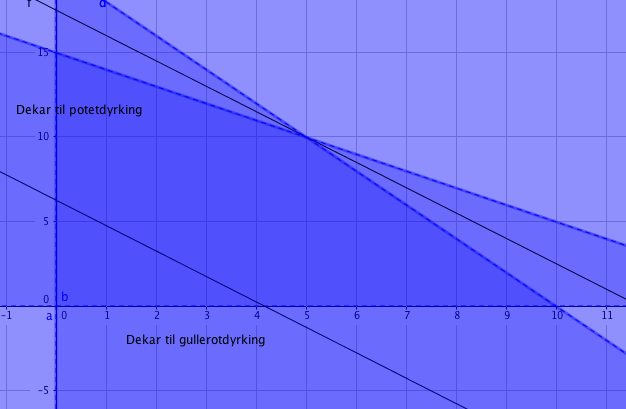
b)
c)
Fra Figuren i b ser man at han bør bruke 5 dekar på gulerøtter, og 10 dekar på poteter, Inntekten blir da 60 000 + 80 000, altså 140 000 kroner.
Laget først en tilfeldig nivålinje basert på 1200x +8000y. Denne ble så parallellforskjøvet til den ytterste begrensningen gitt av ulikhetene. Linjen går da gjennom punktet (5, 10) som er det optimale produksjonsforholdet under de gitte betingelser.
Oppgave 9
$4^x-6\cdot 2^x+8 =0 \\ (2^x)^2-6 \cdot 2^x+8=0 \\ u = 2^x \\ u^2 -6u + 8=0 \\ u= \frac{6 \pm \sqrt{36-32}}{2} \\ u=2 \vee u = 4 \\ 2^x=2 \vee 2^x= 8 \\ 2^x=2 \vee 2^x= 2^3 \\ x=1 \vee x=3 $
DEL TO
Oppgave 1
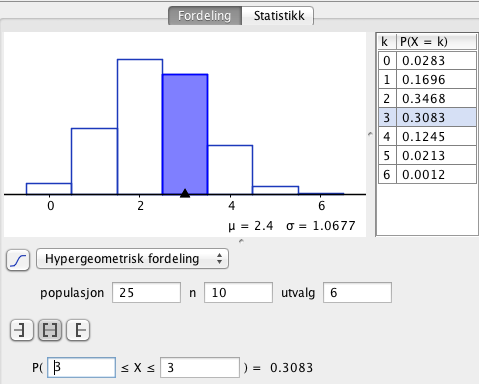
a)
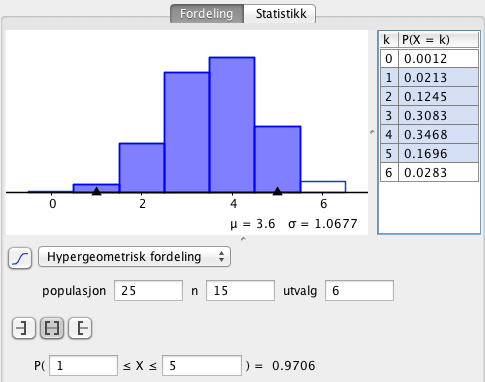
Sannsynligheten for tre jenter og tre gutter blir trukket er 30,8%.
b)
Sannsynlighet for at begge kjønn er representert er:
P (begge kjønn) = 1 - P( bare gutter )- P(bare jenter) = 1 - 0,0012 - 0,0283 = 0,9706
Altså ca. 97%
c)
Vi har tre forskjellige grupper, "Geir", "gutter minus Geir" og "jenter". Geir skal være med, to tilfeldige gutter skal være med, og tre tilfeldige jenter skal være med:
P( Geir er med blant tre jenter og tre gutter)=$ \frac{\binom{1}{1} \binom{9}{2} \binom{15}{3}}{\binom{25}{6}} = 0,0925$
Det er ca. 9,25% sannsynlig at Geir blir med under gitte betingelser.
Oppgave 2
a)
$BMI= \frac{m}{h^2} = \frac{78}{1,77^2} = 24,9$
b)
$BMI= \frac{m}{h^2} \\ h= \sqrt{\frac{85}{28}} = 1,74$
Personen er 174 cm høy.
c)
Terje: masse = m, høyde =h
Svein: masse = (m+4), høyde = (h + 0,04)
Begge med en BMI på 28:
$28 = \frac{m}{b^2} \quad \wedge \quad 28 = \frac{(m+4)}{(h+ 0,04)^2}$
I CAS:
Terje er 1,77 meter høy, med en masse på 87,3 kilogram. Svein har en masse på 91,3 kilogram og en høyde på 1,81 meter.
Oppgave 3
a)
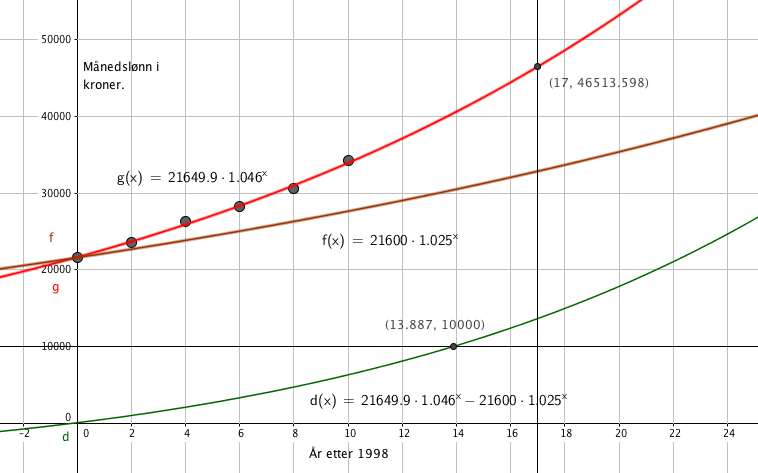
Den prosentvise veksten blir 4,6, i følge modellen.
b)
Lønnen i 2015 blir ca 46 500 kr, i følge modellen.
c)
Se funksjon f i figuren i a.
d)
Funksjon d viser forskjellen mellom de to modellene. I 2012 vil forskjellen være ca. 10 000 kr.
Oppgave 4
a)
Areal:
$A= x \cdot f(x) = x \cdot \frac{5}{x^2+2} = \frac{5x}{x^2+2}$
b)
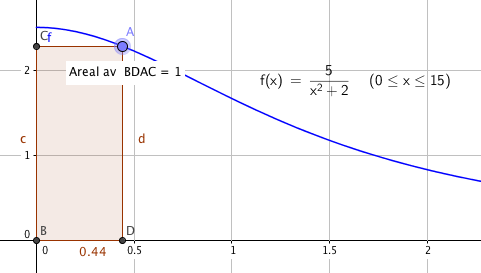
Tegner grafen i Geogebra og legger et glidende punkt på den. Ser da at det er to x verdier som gir oss areal lik en:
x= 0,44 og x= 4,59 gir rektangelet arealet lik 1.
c)
Arealet blir størst når x er lik kvadratroten av to. Da er arealet $\frac{5 \cdot \sqrt{2}}{4}$.