R1 2016 vår LØSNING: Forskjell mellom sideversjoner
| (37 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 66: | Linje 66: | ||
$f´(x)=0 \\ x= -1 \vee x=0 \vee x=1$ | $f´(x)=0 \\ x= -1 \vee x=0 \vee x=1$ | ||
Den deriverte er positiv for x < -1, negativ for -1<x<0, positiv for 0<x<1 og negativ for x >1. | |||
Det gir toppunkt for x= -1 og x = 1 og minimum for x = 0. | |||
Topp: (-1, f( -1)) gir (-1,1) og (1,f(1)) gir (1,1) | |||
Bunn: (0, f(0)) gir (0,0) | |||
==c)== | ==c)== | ||
| Linje 74: | Linje 81: | ||
[[File:r1-v2016-13d.png]] | [[File:r1-v2016-13d.png]] | ||
Grafen til f har fire vendepunkter. | |||
==Oppgave 4== | ==Oppgave 4== | ||
| Linje 103: | Linje 112: | ||
===c)=== | ===c)=== | ||
Det er to muligheter: AB || CD eller BC || AD. | |||
$[4, 1] = s[-3, t-5] \vee [-2, 3]= s[-1, t-1] \\ s= - \frac 43 \Rightarrow - \frac 43(t-5)=1 \vee s =2 \Rightarrow 2(t-1)=3 \\ t= \frac {17}{4} \vee t = \frac 52$ | |||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 187: | Linje 201: | ||
$P(R) = P(F) \cdot P(R|F) + P(\bar{F}) \cdot P(R|\bar{F})=$ | $P(R) = P(F) \cdot P(R|F) + P(\bar{F}) \cdot P(R|\bar{F})= \frac12 \cdot \frac{5}{14} + \frac 12 \cdot \frac{1}{7} = \frac 14$ | ||
===c)=== | ===c)=== | ||
$P(F|R)= \frac{P(F) \cdot P(R|F) }{P(R)} = \frac{\frac{1}{2}\cdot \frac{5}{14}}{\frac {7}{28}} = \frac 57$ | |||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 195: | Linje 211: | ||
===a)=== | ===a)=== | ||
[[File:r1-v16-22a.png]] | |||
===b)=== | |||
Arealet av et rektangel er lengde multiplisert med bredde: | |||
Dersom lengden er x, er bredden f(x), Altså $T(x) = x\cdot f(x) = x \cdot 5e^{-\frac{x}{2}} = 5xe^{- \frac{x}{2}}$ | |||
===c)=== | ===c)=== | ||
$T´(x)= 5e^{- \frac x2} + 5x(- \frac 12) e^{- \frac x2} = (5-2,5x)e^{- \frac x2}$ | |||
Ser at eneste ekstremalpunkt er for x=2 : $T(2) = 10e^{-1} = \frac{10}{e} \approx 3,68$ | |||
Største areal er 3,68, når x=2. | |||
==Oppgave 3== | ==Oppgave 3== | ||
| Linje 206: | Linje 232: | ||
===a)=== | ===a)=== | ||
Parameterfremstilling for linjen l gjennom B og C. Trenger ett punkt og en rettningsvektor: | |||
$\vec{BC} = [1,5]$ og B( 4, 0). | |||
<math> \left[ \begin{align*}x = 4 + t\\ y = 5t \end{align*}\right] </math> | |||
===b)=== | ===b)=== | ||
$\vec {AP}= [4+t-1, 5t-3 ]= [3+t, -3+5t]$ | |||
AP vektor kan jo uttrykkes som x- koordinat til P minus x-koordinat til A, og tilsvarende for y-koordinater. | |||
===c)=== | ===c)=== | ||
$\vec{AB} \cdot \vec{AP} =0 \\ [3, -3] \cdot[3+t, -3+5t ] =0 \\ 9+3t+9-15t=0 \\ t = \frac 32$ | |||
Innsatt i parameterfremstillingen i a gir det $P(\frac{11}{2}, \frac{15}{2} )$ | |||
===d)=== | ===d)=== | ||
[[File:r1-v16-23d.png]] | |||
Innsatt i parameterfremstillingen i a får man: | |||
$P_1 (4+(-4),5(-3))= (-1, 15)$ | |||
og | |||
$P_2 ( 4+0,6, 5 \cdot 0,6 )= (\frac{23}{5}, 3)$ | |||
==Oppgave 4== | ==Oppgave 4== | ||
| Linje 218: | Linje 268: | ||
===a)=== | ===a)=== | ||
Vi skal finne likningen til linje $l_1$ når vi vet at denne står vinkelrett på linjen gjennom B og C. | |||
Stigningstall til linjen gjennom BC: $ \frac{\frac 1t - \frac 1s}{t-s} = \frac{s-t}{(t-s)st}$ | |||
Siden $l_1$ er vinkelrett på BC blir stigningstallet til $l_1$: $ a_l = - \frac {1}{AB} = - \frac{(t+s)st}{s-t} = st$ | |||
Likningen for $l_1$ blir da: $y-y_1=st(x-x_1)\\ y- \frac 1r = st(x-r) \\ y= st(x-r)+ \frac 1r$ | |||
===b)=== | ===b)=== | ||
[[File:r1-v16-24b.png]] | |||
Funksjonen er $f(x)= \frac 1x$. Vi ser at innsatt x verdi gir oss y verdi, altså vil alltid skjæringspunktet mellom linjene ligge på grafen. | |||
Siste sideversjon per 22. sep. 2016 kl. 08:59
Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du har kommentarer til løsningsforslaget. På forhånd, takk.
Løsningsforslag (pdf) fra bruker LektorH.
Løsningsforslag (pdf) fra bruker Claves
DEL EN
Oppgave 1
a)
$f(x)=-3x^2+6x-4$
$f'(x)=-6x+6= -6(x-1)$
b)
$g(x)=5\ln(x^3-x)$
$g'(x)=\frac{5(3x^2-1)}{x^3-x}=\frac{15x^2-5}{x^3-x}$
c)
$h(x)=\frac{x-1}{x+1}$
$h'(x)=\frac{x+1-(x-1)}{(x+1)^2}=\frac{2}{(x+1)^2}$
Oppgave 2
a)
$p(x)=x^3-7x^2+14x+k$
$p(x)$ er delelig med $(x-2)$ hvis og bare hvis $p(2)=0$
$p(2)=8-7\cdot4+14\cdot2+k=8-28+28+k=8+k$
$8+k=0$
$k=-8$
b)
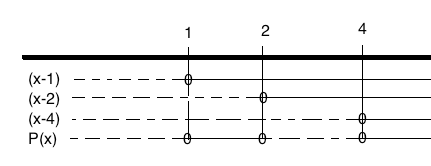
$ \quad x^3-7x^2+14x-8 :(x-2)= x^2 - 5x + 4 \\ -(x^3-2x^2) \\ \quad \quad-5x^2 + 14x -8 \\ \quad \quad -(-5x^2 -10x) \\ \quad \quad \quad \quad \quad (4x -8)$
$x= \frac{5 \pm \sqrt{25 - 16}}{2} \\ x= 1 \vee x =4 \\ \\ P(x)= (x-1)(x-2)(x-4)$
c)
$P(x) \leq 0 $
$x \in < \leftarrow,1] \cup [2,4]$
Oppgave 3
a)
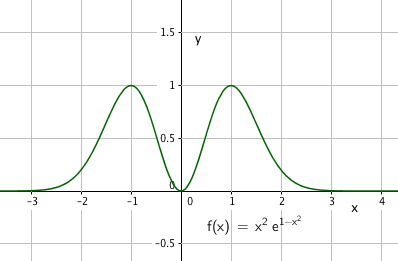
$f(x)=x^2e^{1-x^2}$
$f'(x)=2xe^{1-x^2}+x^2\cdot-2xe^{1-x^2}=2xe^{1-x^2}(1-x^2)$
b)
$f´(x)=0 \\ x= -1 \vee x=0 \vee x=1$
Den deriverte er positiv for x < -1, negativ for -1<x<0, positiv for 0<x<1 og negativ for x >1. Det gir toppunkt for x= -1 og x = 1 og minimum for x = 0.
Topp: (-1, f( -1)) gir (-1,1) og (1,f(1)) gir (1,1)
Bunn: (0, f(0)) gir (0,0)
c)
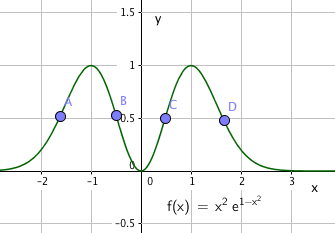
d)
Grafen til f har fire vendepunkter.
Oppgave 4
a)
$AB=AC=BC=6 \ cm$
$HB=\frac{1}{2}AB=3 \ cm$
$CH=\sqrt{(BC)^2-(HB)^2}=\sqrt{6^2-3^2} \ cm=\sqrt{27}=\sqrt{3^3} \ cm=3\sqrt{3} \ cm$
$CF=CE=\sqrt{(BC)^2+(BE)^2}=\sqrt{6^2+6^2} \ cm=\sqrt{2\cdot6^2} \ cm=6\sqrt{2} \ cm$
$HF=\sqrt{(CF)^2-(CH)^2}=\sqrt{72-27} \ cm=\sqrt{45} \ cm=\sqrt{9\cdot5} \ cm=3\sqrt{5} \ cm$
b)
$\frac{AF}{AB}=\frac{3+3\sqrt{5}}{6}=\frac{3(1+\sqrt{5})}{2\cdot3}=\frac{1+\sqrt{5}}{2}=\phi$
Oppgave 5
a)
$\vec{AB} =[5-1,2-1] = [4, 1] \\ \vec{AC} = [3-1, 5-1]=[2,4] \\ \vec{AB} \neq k \vec{AC}$
Punktene A, B og C ligger ikke på en rett linje.
b)
$\vec{CD} = [-3, t - 5] \\ \vec{DA} = [1, 1- t] \\ \vec{CD} \cdot \vec{DA} =0 \\ [-3, t-5] \cdot [ 1, 1-t] = 0 \\ -3 + (t-5)(1-t)= 0 \\ -t^2+6t - 8 = 0 \\ t= 2 \vee t =4$
c)
Det er to muligheter: AB || CD eller BC || AD.
$[4, 1] = s[-3, t-5] \vee [-2, 3]= s[-1, t-1] \\ s= - \frac 43 \Rightarrow - \frac 43(t-5)=1 \vee s =2 \Rightarrow 2(t-1)=3 \\ t= \frac {17}{4} \vee t = \frac 52$
Oppgave 6
a)
Antall mulige fagkombinasjoner med 2 realfag og 2 andre fag:
${5\choose2}\cdot{8\choose2}=\frac{5\cdot4}{2!}\cdot\frac{8\cdot7}{2!}=10\cdot28=280$
b)
Antall mulige fagkombinasjoner med 4 fag hvor minst 2 er realfag:
${5\choose2}\cdot{8\choose2}+{5\choose3}\cdot{8\choose1}+{5\choose4}=280+\frac{5\cdot4\cdot3}{3!}\cdot8+5=280+80+5=365$
Oppgave 7
a)
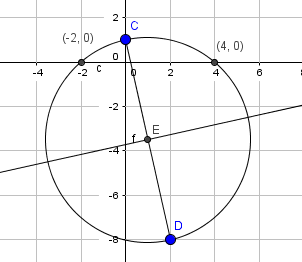
Nullpunktene til f er (-2, 0) og (4, 0).
b)
$f(x)=x^2+px+q$
$A=(0,1)$
$B=(-p,q)$
$\vec{OS}=\vec{OA}+\frac{1}{2}\vec{AB}=[0,1]+\frac{1}{2}[-p,q-1]=[\frac{-p}{2},1+\frac{q-1}{2}]=[\frac{-p}{2},\frac{q+1}{2}]$
$S=(\frac{-p}{2},\frac{q+1}{2})$
$r=|\vec{AS}|=\sqrt{(\frac{-p}{2})^2+(\frac{q-1}{2})^2}=\sqrt{\frac{p^2+(q-1)^2}{4}}=\frac{\sqrt{p^2+(q-1)^2}}{2}$
c)
Likning for sirkel:
$(x-x_1)^2+(y-y_1)^2=r^2$
$(x+\frac{p}{2})^2+(y-\frac{q+1}{2})^2=\frac{p^2+(q-1)^2}{4}$
Skjæring med x-aksen:
$y=0$
$(x+\frac{p}{2})^2+(-\frac{q+1}{2})^2=\frac{p^2+(q-1)^2}{4}$
$(x+\frac{p}{2})^2=\frac{p^2+(q-1)^2}{4}-\frac{(q+1)^2}{4}$
$x+\frac{p}{2}=\frac{\pm \sqrt{p^2-4q}}{2}$
$x=\frac{-p \pm \sqrt{p^2-4q}}{2}$
Nullpunkter til $f(x)$:
$x^2+px+q=0$
$x=\frac{-p \pm \sqrt{p^2-4q}}{2}$
Sirkelen skjærer x-aksen i nullpunktene til $f(x)$.
DEL TO
Oppgave 1
a)
Det er to bunker:
$P(F) = P( \bar{F})= 0,5$
To røde kort fra bunke A:
$ P(R|F) = \frac 58 \cdot \frac 47 = \frac {5}{14}$
To røde kort fra bunke B:
$P(R| \bar{F})= \frac 37 \cdot \frac 26 = \frac 17$
b)
Den totale sannsynligheten for to røde kort:
$P(R) = P(F) \cdot P(R|F) + P(\bar{F}) \cdot P(R|\bar{F})= \frac12 \cdot \frac{5}{14} + \frac 12 \cdot \frac{1}{7} = \frac 14$
c)
$P(F|R)= \frac{P(F) \cdot P(R|F) }{P(R)} = \frac{\frac{1}{2}\cdot \frac{5}{14}}{\frac {7}{28}} = \frac 57$
Oppgave 2
a)
b)
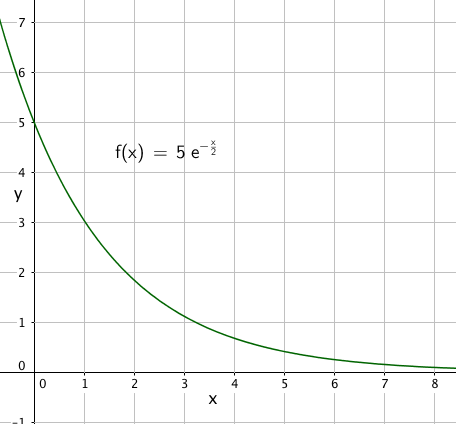
Arealet av et rektangel er lengde multiplisert med bredde:
Dersom lengden er x, er bredden f(x), Altså $T(x) = x\cdot f(x) = x \cdot 5e^{-\frac{x}{2}} = 5xe^{- \frac{x}{2}}$
c)
$T´(x)= 5e^{- \frac x2} + 5x(- \frac 12) e^{- \frac x2} = (5-2,5x)e^{- \frac x2}$
Ser at eneste ekstremalpunkt er for x=2 : $T(2) = 10e^{-1} = \frac{10}{e} \approx 3,68$
Største areal er 3,68, når x=2.
Oppgave 3
a)
Parameterfremstilling for linjen l gjennom B og C. Trenger ett punkt og en rettningsvektor:
$\vec{BC} = [1,5]$ og B( 4, 0).
<math> \left[ \begin{align*}x = 4 + t\\ y = 5t \end{align*}\right] </math>
b)
$\vec {AP}= [4+t-1, 5t-3 ]= [3+t, -3+5t]$
AP vektor kan jo uttrykkes som x- koordinat til P minus x-koordinat til A, og tilsvarende for y-koordinater.
c)
$\vec{AB} \cdot \vec{AP} =0 \\ [3, -3] \cdot[3+t, -3+5t ] =0 \\ 9+3t+9-15t=0 \\ t = \frac 32$
Innsatt i parameterfremstillingen i a gir det $P(\frac{11}{2}, \frac{15}{2} )$
d)
Innsatt i parameterfremstillingen i a får man:
$P_1 (4+(-4),5(-3))= (-1, 15)$ og
$P_2 ( 4+0,6, 5 \cdot 0,6 )= (\frac{23}{5}, 3)$
Oppgave 4
a)
Vi skal finne likningen til linje $l_1$ når vi vet at denne står vinkelrett på linjen gjennom B og C.
Stigningstall til linjen gjennom BC: $ \frac{\frac 1t - \frac 1s}{t-s} = \frac{s-t}{(t-s)st}$
Siden $l_1$ er vinkelrett på BC blir stigningstallet til $l_1$: $ a_l = - \frac {1}{AB} = - \frac{(t+s)st}{s-t} = st$
Likningen for $l_1$ blir da: $y-y_1=st(x-x_1)\\ y- \frac 1r = st(x-r) \\ y= st(x-r)+ \frac 1r$
b)
Funksjonen er $f(x)= \frac 1x$. Vi ser at innsatt x verdi gir oss y verdi, altså vil alltid skjæringspunktet mellom linjene ligge på grafen.