R2 2016 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (7 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://www.matematikk.net/matteprat/download/file.php?id=1321 Oppgaven som pdf] | [http://www.matematikk.net/matteprat/download/file.php?id=1321 Oppgaven som pdf] | ||
[http://www.matematikk.net/matteprat/download/file.php?id=1335 Løsning laget av | [http://www.matematikk.net/matteprat/download/file.php?id=1335 Løsning laget av Dennis Christensen] | ||
[https://ndla.no/sites/default/files/eksamen_r2_h_2016_losning_nb_24.04.2018.pdf Løsning laget av NDLA] | |||
[http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=44287&start=75#p209758 Løsning til del 2 laget av mattepratbruker Kaptein Neseblod] | [http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=44287&start=75#p209758 Løsning til del 2 laget av mattepratbruker Kaptein Neseblod] | ||
| Linje 83: | Linje 85: | ||
$f^{(2)}(x)=- \frac{3 \pi^2}{4} sin( \frac{\pi}{2}x) \quad \quad x \in <0, 12> \\ f^{(2)}(x)=0 \\ sin( \frac{\pi}{2}x) =0 \\ x=2k , \quad k=1,...,5$ | $f^{(2)}(x)=- \frac{3 \pi^2}{4} sin( \frac{\pi}{2}x) \quad \quad x \in <0, 12> \\ f^{(2)}(x)=0 \\ sin( \frac{\pi}{2}x) =0 \\ x=2k , \quad k=1,...,5$ | ||
y verdier: | |||
$f(2k)= 5, \quad k= 1,..., 5$ | |||
Vendepunkter (2k, 5), \quad k = 1, ... , 5 | |||
===d)=== | ===d)=== | ||
| Linje 117: | Linje 125: | ||
==Oppgave 9== | ==Oppgave 9== | ||
==DEL TO== | |||
==Oppgave 1== | |||
===a)=== | |||
t = 0 for år 2015 | |||
Derfor y(0) = 5200000 | |||
Endting er " inn minus ut" : | |||
$y' = 44000 + 0,011y - 0,008y = 0,003y + 44000$ | |||
===b)=== | |||
[[File:r2-h2016-2-1b.png]] | |||
===c)=== | |||
==Oppgave 2== | |||
===a)=== | |||
===b)=== | |||
===c)=== | |||
===d)=== | |||
==Oppgave 3== | |||
===a)=== | |||
===b)=== | |||
===c)=== | |||
===d)=== | |||
==Oppgave 4== | |||
===a)=== | |||
===b)=== | |||
Siste sideversjon per 27. mai 2018 kl. 03:59
Løsning laget av Dennis Christensen
Løsning til del 2 laget av mattepratbruker Kaptein Neseblod
Diskusjon av denne oppgaven på matteprat
DEL EN
Oppgave 1
a)
$f(x)= 3 cos 2x \\ f'(x)= -6sin 2x$
a)
$g(x) = e^{sinx} \\ g'(x)= cosx \cdot e^{sin x} $
c)
$h(x)= \frac{x}{sin x} \\ h'(x)= \frac{sinx - xcosx}{sin^2x } $
Oppgave 2
a)
$\int(x^2-3x+2)dx = \frac 13 x^3- \frac 32x^2+2x+C$
b)
$\int x cos(x)dx = x sin(x) - \int sin(x)dx = x sin(x) - (- cos(x) ) + C = x sin(x) +cos(x)+C$
c)
$\int 2x \cdot sin(x) dx \quad \quad u=x^2, \quad \frac{du}{dx} = 2x \Rightarrow du = 2xdx \\= \int sin(u) du \\ = -cos x^2 + C$
Oppgave 3
a)
Ligningrn for linjen:
Konstantleddet er null siden linjen går gjennom (0, 0). Stigningstallet er endring i y verdi delt på endring i x verdi:
$y= \frac rh x$
b)
Dette er en kjegle med radius r og høyde h:
$V = \pi \int\limits_0^h (f(x))^2 dx = \pi \int\limits_0^h \frac{r^2}{h^2}x^2 dx = \frac{\pi r^2}{h^2} [ \frac 13 x^3]_0^h = \frac 13 \pi r^2h $
Oppgave 4
a)
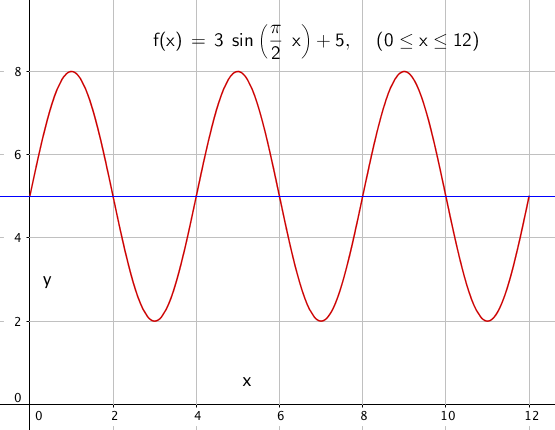
Perioden til f:
$P= \frac{2 \pi}{k} = \frac{2 \pi}{\frac{\pi}{2}} = 4$
b)
Likevektslinje : y= 5
Amplitude: A = 3
$y_{min} = 5-3 =2 \\ y_{maks} = 5+3 = 8$
c)
Vendepunkter:
$f^{(2)}(x)=- \frac{3 \pi^2}{4} sin( \frac{\pi}{2}x) \quad \quad x \in <0, 12> \\ f^{(2)}(x)=0 \\ sin( \frac{\pi}{2}x) =0 \\ x=2k , \quad k=1,...,5$
y verdier:
$f(2k)= 5, \quad k= 1,..., 5$
Vendepunkter (2k, 5), \quad k = 1, ... , 5
d)
Oppgave 5
a)
$ \frac{d^2y}{dx}{ -4 \frac{dy}{dx}+5y =0 \\ \frac {d^2}{dx}e^{rx} -4\frac {d}{dx}e^{rx}}-5 e^{rx}=0 \\r^2 e^{rx} -4r e^{rx} -5 e^{rx} =0 \\ (r^2-4r-5)e^{rx} =0 $
$e^{rx}$ er en løsning når $r^2-4r - 5 =0$
b)
$r^2-4r-5=0 \\ r = -1 \vee r=5 \\ y=C_1e^{-x} + C_2e^{5x}$
c)
Fra initialbetingelsene får vi følgende:
$y(0)=6 \Rightarrow C_1 + C_2 =6 \\ y'(0)=0 \Rightarrow -C_1 + 5C_2=0 \\ C_2=1 \wedge C_1 = 5 \\ y= 5e^{-x} + e^{5x}$
Oppgave 6
Oppgave 7
Oppgave 8
Oppgave 9
DEL TO
Oppgave 1
a)
t = 0 for år 2015
Derfor y(0) = 5200000
Endting er " inn minus ut" :
$y' = 44000 + 0,011y - 0,008y = 0,003y + 44000$