Løsning del 2 utrinn Vår 17: Forskjell mellom sideversjoner
→a): Fikset bildet, la til fremgangsmåte |
|||
| (14 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 19: | Linje 19: | ||
Multiplisere antall personer med frekvens og summerer, deler så på 30: | Multiplisere antall personer med frekvens og summerer, deler så på 30: | ||
Gjennomsnitt = $\frac{13+10+9+16+15+12}{30}= 2, | Gjennomsnitt = $\frac{13+10+9+16+15+12}{30}= 2,5$ | ||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 46: | Linje 46: | ||
Multiplisert med literprisen: $43,5 L \cdot 14,30 kr/ L = 622,05 kr$ | Multiplisert med literprisen: $43,5 L \cdot 14,30 kr/ L = 622,05 kr$ | ||
Han må betale 622 kroner. | |||
===b)=== | ===b)=== | ||
| Linje 59: | Linje 59: | ||
Siden kannen var "tilnærmet lik" et | Siden kannen var "tilnærmet lik" et prisme kan vi si at den tar ca. 20 liter. | ||
===c)=== | ===c)=== | ||
Siden forholdet mellom solgte liter av bensin og solgte liter av diesel var 3: 5, vet vi at det ble solgt 8 deler. Vi deler 28 000 liter på 8 deler for å finne ut hvor stor hver del er. | |||
28 000 liter : 8 = 3 500 liter. | |||
En del er 3 500 liter. | |||
Stasjonen solgte tre deler diesel: $3\cdot 3500 liter = 10 500 liter.$ | |||
og fem deler bensin: $5 \cdot 3500 liter =17500 liter$ | |||
Den dagen solgte bensinstasjonen 10 500 liter diesel og 17 500 bensin. | |||
==Oppgave 4== | ==Oppgave 4== | ||
[[File:ex1-2017.png]] | |||
[[File:ex2-2017.png]] | |||
==Oppgave 5== | ==Oppgave 5== | ||
| Linje 84: | Linje 102: | ||
===a)=== | ===a)=== | ||
$v = \frac st$ gir 1,5h ganger 60 km/h, som er 90 kilometer. | $v = \frac st$ gir $s = t \cdot v$, 1,5h ganger 60 km/h, som er 90 kilometer. | ||
===b)=== | ===b)=== | ||
| Linje 102: | Linje 121: | ||
===a)=== | ===a)=== | ||
[[File:sirkel 2017.png]] | |||
Slik vil figuren se ut når den er tegnet i GeoGebra. Fremgangsmåte: | |||
Tegn et linjestykke med lengde 10 (AB), lag vinkelen i A og et linjestykke med lengde 5 på vinkelen (AC). Trekk linjestykke BC. | |||
Lag midtnormalen til AB med funksjonen midtnormal[<linjestykke>]. Merk skjæringspunktet S. | |||
Tegn sirkelen med sentrum i S. | |||
===b)=== | ===b)=== | ||
| Linje 110: | Linje 138: | ||
Finner arealet av sirkelen og trekker fra arealet av trekanten. | Finner arealet av sirkelen og trekker fra arealet av trekanten. | ||
Areal av sirkel | |||
$A = \pi r^2 = \pi \cdot 5^2 \approx 78,5$ | |||
Areal av trekant | |||
$A = \frac{g \cdot h}{2}$ | |||
For å regne ut arealet av trekanten trenger vi en høyde. La AC være grunnflaten, da blir BC høyden, den kan vi finne ved Pytagoras. | |||
$5^2 + BC^2 = 10^2 \\ BC = \sqrt{100-25} \approx 8,7$ | |||
Nå kan vi regne ut arealet av trekanten | |||
$A = \frac{5 \cdot 8,7}{2} = 21,8$ | |||
Arealet av det blå området blir da | |||
$78,5 - 21,8 = 56,7$ cm$^2$ | |||
==Oppgave 8== | ==Oppgave 8== | ||
Siste sideversjon per 22. jun. 2017 kl. 16:44
DEL TO
Oppgave 1
a)
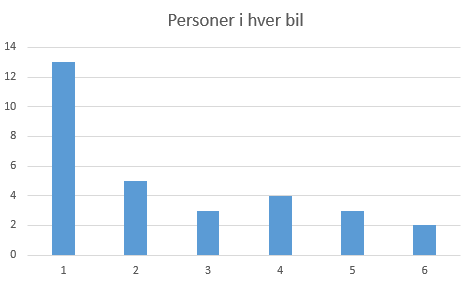
Totalt 30 biler.
b)
Typetall er den det verdi det er mest av, altså 1 (en).
Median av 30 verdier er gjennomsnitt av verdi 15 og 16 når verdiene er organisert i stigende rekkefølge. Vi ser at både nr. 15 og 16 har verdi 2 (to).
c)
Multiplisere antall personer med frekvens og summerer, deler så på 30:
Gjennomsnitt = $\frac{13+10+9+16+15+12}{30}= 2,5$
Oppgave 2
a)
Det er 24 km (leser av kurven).
b)
Fra 11:45 til 12:15, en halv time.
c)
De bruker 1,25 timer på 24 km.
$v = \frac{24 km}{1,25t} = 19,2 km/t$
De har en gjennomsnittsfart på 19,2 km / time.
Oppgave 3
a)
Han trenger (60-16,5)L = 43,5 L
Multiplisert med literprisen: $43,5 L \cdot 14,30 kr/ L = 622,05 kr$
Han må betale 622 kroner.
b)
Husk at en liter er det samme volumet som 1$dm^3$.
Vi gjør lengdemålene på kanna om til dm og multipliserer ut:
$V= l \cdot b \cdot h = 3,20 dm \cdot 1,5dm \cdot 4,20 dm = 20,16 dm^3$
Siden kannen var "tilnærmet lik" et prisme kan vi si at den tar ca. 20 liter.
c)
Siden forholdet mellom solgte liter av bensin og solgte liter av diesel var 3: 5, vet vi at det ble solgt 8 deler. Vi deler 28 000 liter på 8 deler for å finne ut hvor stor hver del er.
28 000 liter : 8 = 3 500 liter.
En del er 3 500 liter.
Stasjonen solgte tre deler diesel: $3\cdot 3500 liter = 10 500 liter.$
og fem deler bensin: $5 \cdot 3500 liter =17500 liter$
Den dagen solgte bensinstasjonen 10 500 liter diesel og 17 500 bensin.
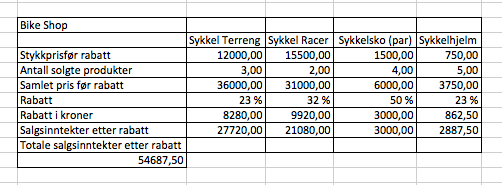
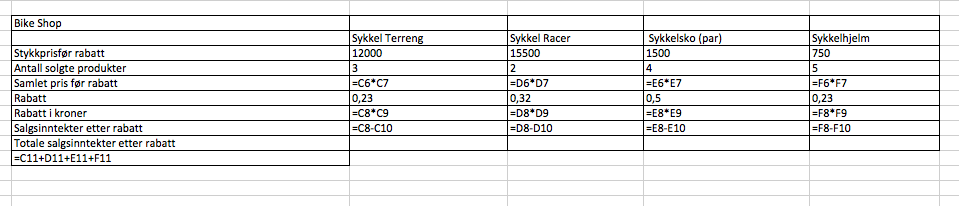
Oppgave 4
Oppgave 5
a)
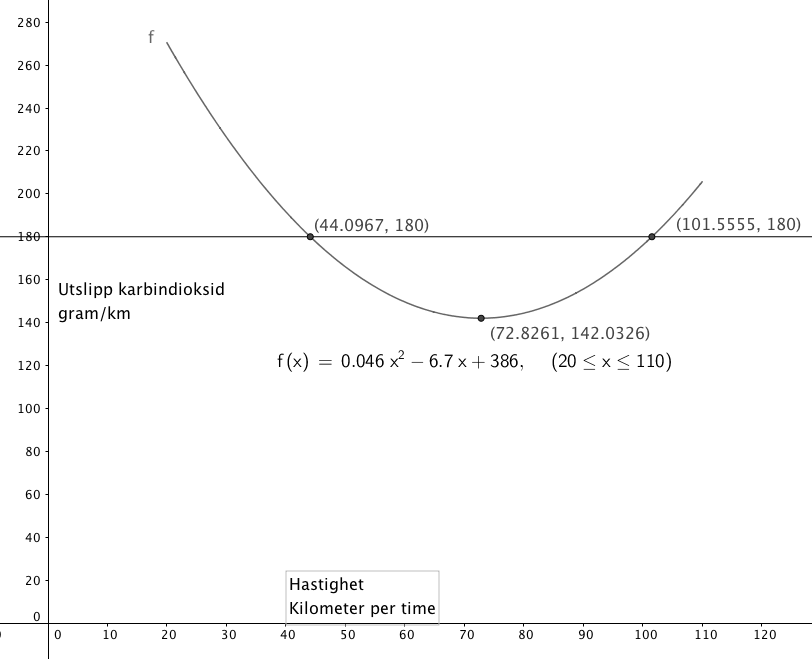
b)
Fra figuren i a ser man at 44 km/t og 102 km /t gir utslipp på 180 g/km.
c)
Finner ekstremalpunktet i Geogebra. Ser at ved 73 km/t er utslippe lavest, da 142 g/km.
Oppgave 6
a)
$v = \frac st$ gir $s = t \cdot v$, 1,5h ganger 60 km/h, som er 90 kilometer.
b)
$s= \frac{v^2}{19,62\cdot f} = \frac{(21 m/s)^2}{19,62\cdot 0,9} =24,97 \approx 25 $
Bremselengden er ca. 25 meter.
c)
$ s = \frac{v^2}{19,62\cdot f} \\ v^2 =19,62 \cdot f \cdot s \\ v = \sqrt{19, 62 \cdot f \cdot s} \\ v= \sqrt{19, 62 \cdot 0,6 \cdot 15 } = 13,3 $
Farten er ca. 13,3 meter per sekund.
Oppgave 7
a)
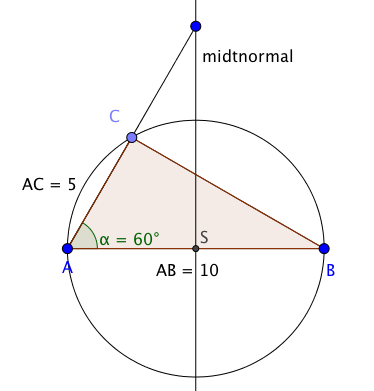
Slik vil figuren se ut når den er tegnet i GeoGebra. Fremgangsmåte:
Tegn et linjestykke med lengde 10 (AB), lag vinkelen i A og et linjestykke med lengde 5 på vinkelen (AC). Trekk linjestykke BC.
Lag midtnormalen til AB med funksjonen midtnormal[<linjestykke>]. Merk skjæringspunktet S.
Tegn sirkelen med sentrum i S.
b)
Vinkel C har toppunkt på sirkelpereferien og spenner over sirkelens diameter. Slike vinkler er alltid 90 grader.
c)
Finner arealet av sirkelen og trekker fra arealet av trekanten.
Areal av sirkel
$A = \pi r^2 = \pi \cdot 5^2 \approx 78,5$
Areal av trekant
$A = \frac{g \cdot h}{2}$
For å regne ut arealet av trekanten trenger vi en høyde. La AC være grunnflaten, da blir BC høyden, den kan vi finne ved Pytagoras.
$5^2 + BC^2 = 10^2 \\ BC = \sqrt{100-25} \approx 8,7$
Nå kan vi regne ut arealet av trekanten
$A = \frac{5 \cdot 8,7}{2} = 21,8$
Arealet av det blå området blir da
$78,5 - 21,8 = 56,7$ cm$^2$
Oppgave 8
a)
Når klaffene er åpne dannes et trapes betående av tre likesidede trekanter. AB er den korte parallelle siden i trapeset. AB er også en side i en av de likesidede trekanten og siden en klaff er 30 meter må også AB være 30 meter.
b)
Høyden fra topp av klaff til lukket bro:
Har en 30, 60, 90 trekant og kan bruke Pytagoras for å finne høyden:
$h = \sqrt{30^2- 15^2} m \approx 26$ meter
Så legger vi til de 8 meterne ned til vannflaten og får ca. 34 meter.
Oppgave 9
a)
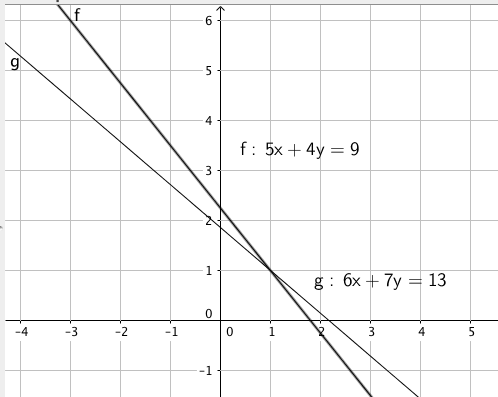
Grafisk løsning i Geogebra gir x = 1 og y = 1.
b)
$x = \frac{ce-bf}{ae-bd} = \frac{9 \cdot 7-4 \cdot 13}{5 \cdot 7 - 4 \cdot 6} = \frac {11}{11} = 1 \\ y = \frac{af-cd}{ae-bd} = \frac{5 \cdot 13- 9 \cdot 6}{5 \cdot 7 - 4 \cdot 6} = \frac {11}{11} = 1$
c)
Bruker innsettingsmetoden.
$x = \frac{c-by}{a}$
Setterinn for x i andre likning:
$d( \frac{c-by}{a})+ey = f \\ dc -bdy +aey = af \\ y(ae - bd) = af - dc \\ y = \frac{af-cd}{ae-bd}$
Gjør tillsvarende for å finne x:
$y = \frac{c-ax}{b}$
Setter inn:
$ dx + e( \frac{c - ax}{b}) = f \\ bdx + ce - aex = bf \\ x = \frac{ce-bf}{ae-bd} $