1T 2017 vår LØSNING: Forskjell mellom sideversjoner
| (66 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 18: | Linje 18: | ||
$\frac{0,72 \cdot 10^8}{60 \cdot 10^{-8}} = \frac{72 \cdot 10^6}{6 \cdot 10^{-7}} = 12 \cdot 10^{6+7} = 1,2 \cdot 10^{14}$ | $\frac{0,72 \cdot 10^8}{60 \cdot 10^{-8}} = \frac{72 \cdot 10^6}{6 \cdot 10^{-7}} = 12 \cdot 10^{6+7} = 1,2 \cdot 10^{14}$ | ||
==Oppgave 2== | |||
$4^0 + 2^{-3} \cdot (2^3)^2 = 1+ 2^3 = 9$ | $4^0 + 2^{-3} \cdot (2^3)^2 = 1+ 2^3 = 9$ | ||
| Linje 26: | Linje 26: | ||
$\sqrt{20} + \sqrt 5 - \frac{\sqrt{160}}{\sqrt 2}= 2 \sqrt 5 +\sqrt 5 - \frac{\sqrt4 \cdot \sqrt4 \cdot \sqrt 2 \cdot \sqrt 5}{\sqrt 2} \\ 2 \sqrt 5 + \sqrt5 - 4 \sqrt 5 = - \sqrt 5$ | $\sqrt{20} + \sqrt 5 - \frac{\sqrt{160}}{\sqrt 2}= 2 \sqrt 5 +\sqrt 5 - \frac{\sqrt4 \cdot \sqrt4 \cdot \sqrt 2 \cdot \sqrt 5}{\sqrt 2} \\ 2 \sqrt 5 + \sqrt5 - 4 \sqrt 5 = - \sqrt 5$ | ||
==Oppgave 4== | |||
<math> \left[ \begin{align*}x^2+y^2= 4 \\ x+2 = y \end{align*}\right] </math> | |||
===Oppgave 5=== | Setter inn uttrykket for y i første ligning: | ||
$x^2 + (x+2)^2 = 4 \\ x^2 + x^2 +4x +4 = 4 \\2x(x+2)=0 \\ x= 0 \vee x=-2$ | |||
Setter inn for x i en av ligningene og får følgende to løsningssett: (0, 2) eller (-2, 0) | |||
==Oppgave 5== | |||
$lg(x^2 + \frac 34) = 0 \\ 10^{lg(x^2 + \frac 34)} 10^0 \\ x^2 + \frac 34 =1 \\ x = \pm \frac 12$ | |||
===Oppgave 6=== | ===Oppgave 6=== | ||
$ \frac{1}{x} + \frac {x-5}{x-1}- \frac{2x-6}{x^2-x} = \\ \frac {}{}\frac{x-1}{x(x-1)} + \frac {x(x+5)}{x(x-1)} - \frac{2x-6}{x(x-1)} = \\ \frac {x-1+x(x-5) -2x +6}{x(x-1} = \\ \frac{x^2-6x+5}{x(x-1)}= \\ \frac {(x-1)(x-5)}{x(x-1)} = \\ \frac{x-5}{x} $ | |||
===Oppgave 7=== | ===Oppgave 7=== | ||
===Oppgave 9=== | ===a)=== | ||
{| width="auto" | |||
| | |||
|Papir | |||
|ikke papir | |||
|Total | |||
|- | |||
|Nett | |||
|32 | |||
|48 | |||
|80 | |||
|- | |||
|Ikke nett | |||
|18 | |||
|2 | |||
|20 | |||
|- | |||
|Total | |||
|50 | |||
|50 | |||
|100 | |||
|} | |||
===b)=== | |||
Både nett og papir: | |||
P ( nett $\cap$ papir) = 32% (leser direkte fra tabell). | |||
===c)=== | |||
Sannsynlighet for ikke papir, gitt nett: | |||
P( ikke papir | nett) = $\frac{P( nett \quad \cap \quad ikke papir)}{P( nett)} = \frac{48}{80} = 0,6$ | |||
==Oppgave 8== | |||
Den lengste siden i en rettvinklet trekant er hypotenusen. Kaller den for x: | |||
$ x^2 = (x-2)^2+ 20^2 \\ x^2 = x^2-4x+4 + 400\\ 4x= 404 \\ x = 101$ | |||
Den lengste siden er 101. | |||
==Oppgave 9== | |||
===a)=== | |||
Gjennomsnittlig vekstfart i intervallet: | |||
$f(-2)= -8+12+4-3 = 5 \\ f(0)= -3 \\ \frac{f(0) - f(-2)}{2} = \frac{-3-5}{2} = -4$ | |||
===b)=== | |||
Momentan vekstfart for f når x = 2. | |||
$f´(x)= 3x^2+ 6x-2 \\ f´(-2) = 12-12--2 = -2$ | |||
==Oppgave 10== | ==Oppgave 10== | ||
| Linje 64: | Linje 134: | ||
===c)=== | ===c)=== | ||
V finner den x verdi som gir f´(x) = 2. | |||
$f´(x) =2 \\ 2x-4 =2 \\ x=3$ | |||
Vi vet at f(3) = 0 | |||
Likningen for tangenten blir da: | |||
$y = ax + b \\ 0 = 2 \cdot 3 + b \\ b = -6$ | |||
y= 2x - 6 er likningen for tangenten med stigningstall 2. | |||
[[File:1T-17-1-10b-2.png]] | [[File:1T-17-1-10b-2.png]] | ||
===d)=== | ===d)=== | ||
Se tangent i c. Likningen blir y = -2x + 2, fordi grafen skjærer y aksen i 2 og avtar med 2 for hver enhet mot høyre. | |||
===e)=== | ===e)=== | ||
Det er oppgitt at tangenten går gjennom (2, -2). Pga symmetri må den også gå gjennom (1,0). | |||
Den deriverte blir da -2 : y = -2x + b som innsatt for (1, 0) gir b = 2, altså er ligningen for tangenten riktig. | |||
==Oppgave 12== | ==Oppgave 12== | ||
===a)=== | |||
Sin (vinkel) = motstående katet delt på hypotenus: $Sin (30^{ \circ}) = \frac 12$ | |||
Cos (vinkel) = hosliggende katet delt på hypotenus: $Cos (30^{\circ}) = \frac{\sqrt{2^2-1^2}}{2} = \frac{\sqrt{3}}{2} \quad$ (her brukte vi pytagoras for å finne hosliggende katet) | |||
Tan (vinkel) = Sin (vinkel) delt på Cos (vinkel): $ Tan (30^{\circ}) = \frac{\frac{1}{2}}{\frac{\sqrt3}{2}} = \frac{1}{\sqrt3} = \frac{\sqrt 3}{3}$ | |||
===b)=== | |||
Bruker arealformenlen: | |||
$A = \frac12 \cdot 2 \cdot 4 \cdot \sin(30) = 2$ | |||
Arealet av trekanten er 2. | |||
===c)=== | |||
Bruker cosinussetningen: | |||
$(BC)^2 =4 + 16 - 2 \cdot 2 \cdot 4 \frac{\sqrt3}{2} = 20 - 8 \sqrt3 = 4(5 - 2\sqrt3) \\ BC = \sqrt{4(5 - 2\sqrt3)} = 2 \sqrt{5-2\sqrt3}$ | |||
==DEL TO== | |||
==Oppgave1== | |||
===a)=== | |||
[[File:1T-17-2-1a.png]] | |||
===b)=== | |||
Fyllingsgraden er under 60% fra uke 4 til 27, altså ca 23 uker. Da er fyllingsgraden over resten av tiden, ca. 29 uker. | |||
===c)=== | |||
Fra Figuren ser man at fyllingsgraden var lavest i uke 14, ca. 35,3%. | |||
===d)=== | |||
Fra Grafen i a ser man at stigningstallet er 2,48. Det betyr at magasinet økte 2,48 prosentpoen i uke 22. | |||
Ved regning: | |||
$f'(x)= -0,0141x^2+0,80x-8,3 \\ f'(22)= 2,48 \\ f(22) = 46,95$ | |||
Likningenblir da: | |||
$y = ax + b \\ 46,95 = 2,48 \cdot22 +b \\ b = -7,6 \\ dvs. \\ y = 2,48x - 7,6$ | |||
==Oppgave 2== | |||
Barn koster x, voksen koster (x + 40): | |||
$2(x + 40 )+ 3x = 520 \\ 5x = 440 \\ x = 88$ | |||
Det koster 88 kroner for barn og 128 kroner for voksne. | |||
==Oppgave 3== | |||
===a)=== | |||
[[File:1T-17-2-3a.png]] | |||
Med geogebra får man f(x) = - 0,94x +30. Siden det er en modell kan man si ca. -x +30, dvs. at andelen dagsrøykere synker med ca. ett prosentpoeng i året. | |||
===b)=== | |||
Ut på høsten i 2026 vil bedriften være nede i 5% i følge modellen ( som trolig ikke har et så stort gyldighetsområde). | |||
==Oppgave 4== | |||
===a)=== | |||
Lager et valgtre: | |||
[[File:1T-17-2-4ab.png]] | |||
P(lekk)= $ \frac{80+25}{300} = 0,35$ | |||
Det er 35% sannsynlig at den er lekk ( ikke tett). | |||
===b)=== | |||
Gitt lekk (ikke tett): | |||
P ( lettmelk) $\frac{80}{80+25} = 0,7619$ som er ca 76,2% | |||
==Oppgave 5== | |||
Vi bruker cosinussettningen. | |||
[[File:1T-17-2-5.png]] | |||
$s = \frac 83$ (utelukker de to andre.) | |||
==Oppgave 6== | |||
[[File:1T-17-2-6-1.png]] | |||
*Fra linje tre ser man at (a, f(a)) er ett nullpunkt. | |||
*Fra linje seks ser man at f'(x) = 0 gi x = a som en løsning, derfor er P også et stasjonært punkt. | |||
*Vi ser at den deriverte vender sin hule side opp, og har to nullpunkter. Da må den skifte fortegn fra negativ til positiv i P, som da altså er et minimumspunkt. | |||
[[File:1T-17-2-6-2.png]] | |||
a lik 2,3 | |||
[[File:1T-17-2-6-3.png]] | |||
Slik går det når a vokser,,, | |||
==Oppgave 7== | |||
===a)=== | |||
Pytagoras: | |||
$(R+r)^2 = R^2 + (2R-r)^2 \\ R^2+ 2Rr + r^2 = R^2 + 4R^2 - 4Rr +r^2 \\ 6Rr = 4R^2 \\ r = \frac 23R$ | |||
===b)=== | |||
Arealet av det grå (blå) feltet er arealet av kvartsirkelen minus arealene av de to halvsirklene. | |||
$A = \frac{\pi(2R)^2}{4} - \frac{\pi R^2}{2} -\frac{\pi( \frac{2R}{3})^2}{2} \\ A = \pi R^2- \frac{9 \pi R^2}{18} - \frac{4 \pi R^2}{18} \\ A = \frac{5 \pi R^2}{18}$ | |||
[[File:1T-17-2-7b.png]] | |||
Siste sideversjon per 24. jun. 2017 kl. 14:39
Løsning laget av mattepratbruker Lektor Nilsen
Løsning bidratt av Lektor Ørjan Augedal, Fana privat gymnas
Løsning laget av mattepratbruker rekel
Løsning laget av mattepratbruker mattemarkus
DEL EN
Oppgave 1
$\frac{0,72 \cdot 10^8}{60 \cdot 10^{-8}} = \frac{72 \cdot 10^6}{6 \cdot 10^{-7}} = 12 \cdot 10^{6+7} = 1,2 \cdot 10^{14}$
Oppgave 2
$4^0 + 2^{-3} \cdot (2^3)^2 = 1+ 2^3 = 9$
Oppgave 3
$\sqrt{20} + \sqrt 5 - \frac{\sqrt{160}}{\sqrt 2}= 2 \sqrt 5 +\sqrt 5 - \frac{\sqrt4 \cdot \sqrt4 \cdot \sqrt 2 \cdot \sqrt 5}{\sqrt 2} \\ 2 \sqrt 5 + \sqrt5 - 4 \sqrt 5 = - \sqrt 5$
Oppgave 4
<math> \left[ \begin{align*}x^2+y^2= 4 \\ x+2 = y \end{align*}\right] </math>
Setter inn uttrykket for y i første ligning:
$x^2 + (x+2)^2 = 4 \\ x^2 + x^2 +4x +4 = 4 \\2x(x+2)=0 \\ x= 0 \vee x=-2$
Setter inn for x i en av ligningene og får følgende to løsningssett: (0, 2) eller (-2, 0)
Oppgave 5
$lg(x^2 + \frac 34) = 0 \\ 10^{lg(x^2 + \frac 34)} 10^0 \\ x^2 + \frac 34 =1 \\ x = \pm \frac 12$
Oppgave 6
$ \frac{1}{x} + \frac {x-5}{x-1}- \frac{2x-6}{x^2-x} = \\ \frac {}{}\frac{x-1}{x(x-1)} + \frac {x(x+5)}{x(x-1)} - \frac{2x-6}{x(x-1)} = \\ \frac {x-1+x(x-5) -2x +6}{x(x-1} = \\ \frac{x^2-6x+5}{x(x-1)}= \\ \frac {(x-1)(x-5)}{x(x-1)} = \\ \frac{x-5}{x} $
Oppgave 7
a)
| Papir | ikke papir | Total | |
| Nett | 32 | 48 | 80 |
| Ikke nett | 18 | 2 | 20 |
| Total | 50 | 50 | 100 |
b)
Både nett og papir:
P ( nett $\cap$ papir) = 32% (leser direkte fra tabell).
c)
Sannsynlighet for ikke papir, gitt nett:
P( ikke papir | nett) = $\frac{P( nett \quad \cap \quad ikke papir)}{P( nett)} = \frac{48}{80} = 0,6$
Oppgave 8
Den lengste siden i en rettvinklet trekant er hypotenusen. Kaller den for x:
$ x^2 = (x-2)^2+ 20^2 \\ x^2 = x^2-4x+4 + 400\\ 4x= 404 \\ x = 101$
Den lengste siden er 101.
Oppgave 9
a)
Gjennomsnittlig vekstfart i intervallet:
$f(-2)= -8+12+4-3 = 5 \\ f(0)= -3 \\ \frac{f(0) - f(-2)}{2} = \frac{-3-5}{2} = -4$
b)
Momentan vekstfart for f når x = 2.
$f´(x)= 3x^2+ 6x-2 \\ f´(-2) = 12-12--2 = -2$
Oppgave 10
a)
$f(x)>0 \Rightarrow x \in <4, \rightarrow>$
b)
$f´(x) >0 \Rightarrow x \in < \leftarrow,1> \cup <3, \rightarrow>$
Oppgave 11
a)
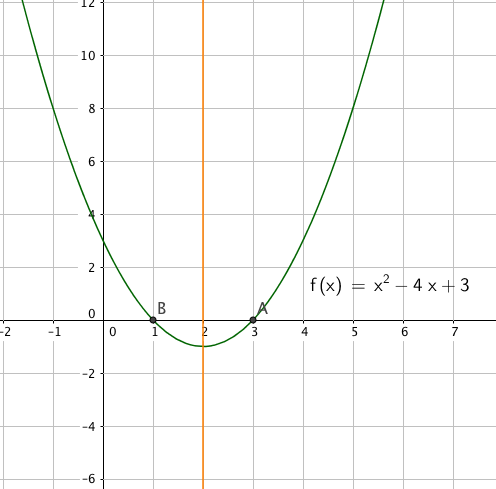
Nullpunkter:
$ f(x)=0 \\ x^2-4x+3=0 \\ x= \frac{4 \pm \sqrt{16 - 4 \cdot 3}}{2} \\ x = 1 \vee x= 3$
Nullpunkter (1,0) og (3,0).
b)
c)
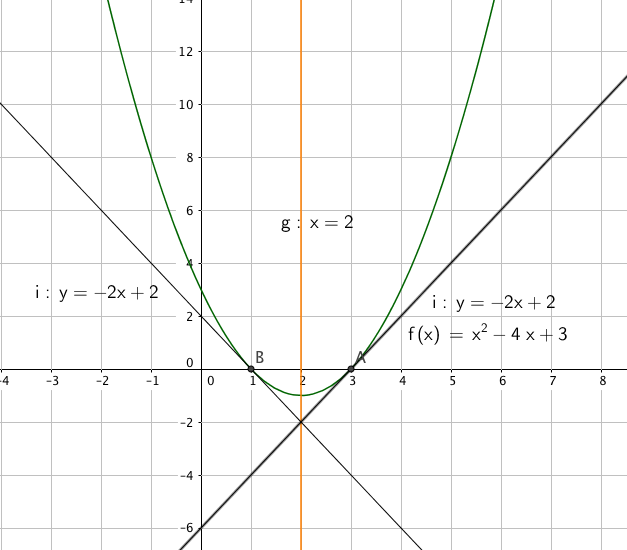
V finner den x verdi som gir f´(x) = 2. $f´(x) =2 \\ 2x-4 =2 \\ x=3$
Vi vet at f(3) = 0
Likningen for tangenten blir da: $y = ax + b \\ 0 = 2 \cdot 3 + b \\ b = -6$
y= 2x - 6 er likningen for tangenten med stigningstall 2.
d)
Se tangent i c. Likningen blir y = -2x + 2, fordi grafen skjærer y aksen i 2 og avtar med 2 for hver enhet mot høyre.
e)
Det er oppgitt at tangenten går gjennom (2, -2). Pga symmetri må den også gå gjennom (1,0).
Den deriverte blir da -2 : y = -2x + b som innsatt for (1, 0) gir b = 2, altså er ligningen for tangenten riktig.
Oppgave 12
a)
Sin (vinkel) = motstående katet delt på hypotenus: $Sin (30^{ \circ}) = \frac 12$
Cos (vinkel) = hosliggende katet delt på hypotenus: $Cos (30^{\circ}) = \frac{\sqrt{2^2-1^2}}{2} = \frac{\sqrt{3}}{2} \quad$ (her brukte vi pytagoras for å finne hosliggende katet)
Tan (vinkel) = Sin (vinkel) delt på Cos (vinkel): $ Tan (30^{\circ}) = \frac{\frac{1}{2}}{\frac{\sqrt3}{2}} = \frac{1}{\sqrt3} = \frac{\sqrt 3}{3}$
b)
Bruker arealformenlen:
$A = \frac12 \cdot 2 \cdot 4 \cdot \sin(30) = 2$
Arealet av trekanten er 2.
c)
Bruker cosinussetningen:
$(BC)^2 =4 + 16 - 2 \cdot 2 \cdot 4 \frac{\sqrt3}{2} = 20 - 8 \sqrt3 = 4(5 - 2\sqrt3) \\ BC = \sqrt{4(5 - 2\sqrt3)} = 2 \sqrt{5-2\sqrt3}$
DEL TO
Oppgave1
a)
b)
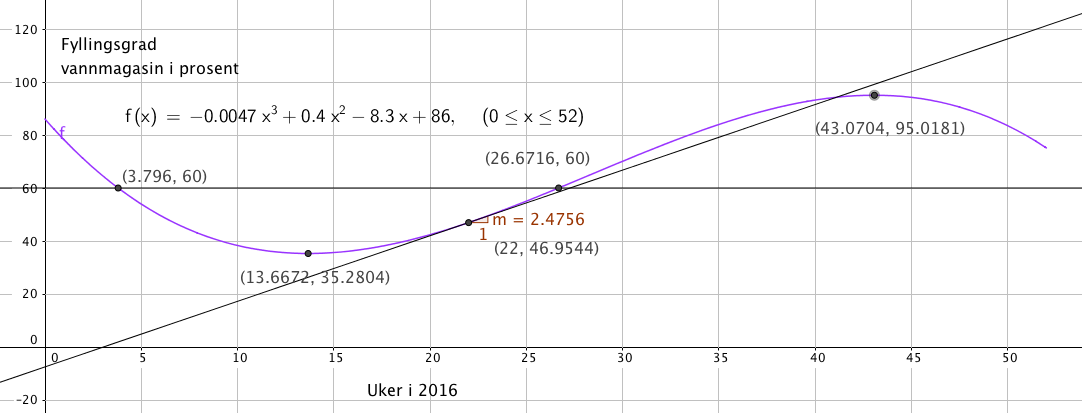
Fyllingsgraden er under 60% fra uke 4 til 27, altså ca 23 uker. Da er fyllingsgraden over resten av tiden, ca. 29 uker.
c)
Fra Figuren ser man at fyllingsgraden var lavest i uke 14, ca. 35,3%.
d)
Fra Grafen i a ser man at stigningstallet er 2,48. Det betyr at magasinet økte 2,48 prosentpoen i uke 22.
Ved regning:
$f'(x)= -0,0141x^2+0,80x-8,3 \\ f'(22)= 2,48 \\ f(22) = 46,95$
Likningenblir da:
$y = ax + b \\ 46,95 = 2,48 \cdot22 +b \\ b = -7,6 \\ dvs. \\ y = 2,48x - 7,6$
Oppgave 2
Barn koster x, voksen koster (x + 40):
$2(x + 40 )+ 3x = 520 \\ 5x = 440 \\ x = 88$
Det koster 88 kroner for barn og 128 kroner for voksne.
Oppgave 3
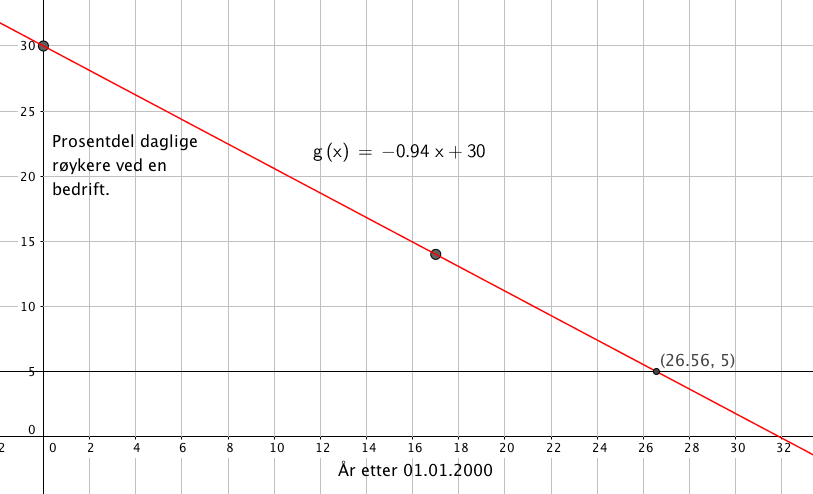
a)
Med geogebra får man f(x) = - 0,94x +30. Siden det er en modell kan man si ca. -x +30, dvs. at andelen dagsrøykere synker med ca. ett prosentpoeng i året.
b)
Ut på høsten i 2026 vil bedriften være nede i 5% i følge modellen ( som trolig ikke har et så stort gyldighetsområde).
Oppgave 4
a)
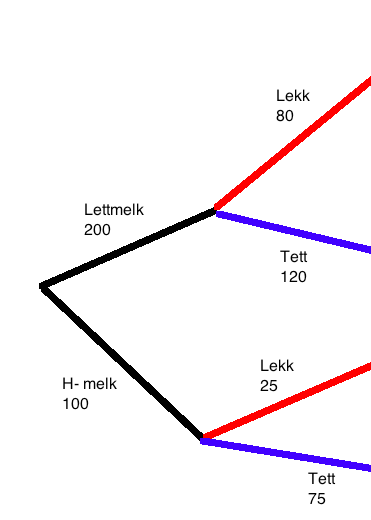
Lager et valgtre:
P(lekk)= $ \frac{80+25}{300} = 0,35$
Det er 35% sannsynlig at den er lekk ( ikke tett).
b)
Gitt lekk (ikke tett):
P ( lettmelk) $\frac{80}{80+25} = 0,7619$ som er ca 76,2%
Oppgave 5
Vi bruker cosinussettningen.
$s = \frac 83$ (utelukker de to andre.)
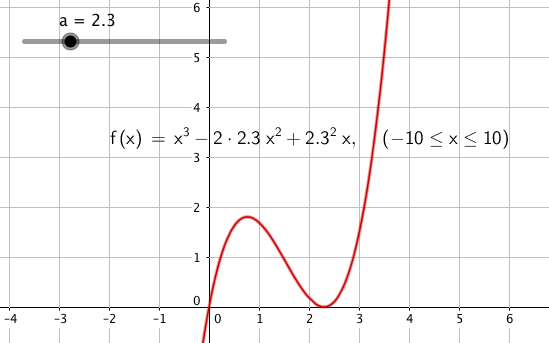
Oppgave 6
- Fra linje tre ser man at (a, f(a)) er ett nullpunkt.
- Fra linje seks ser man at f'(x) = 0 gi x = a som en løsning, derfor er P også et stasjonært punkt.
- Vi ser at den deriverte vender sin hule side opp, og har to nullpunkter. Da må den skifte fortegn fra negativ til positiv i P, som da altså er et minimumspunkt.
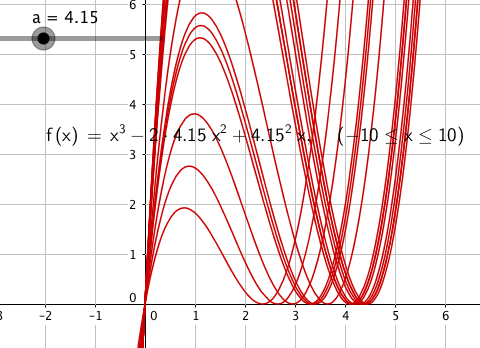
a lik 2,3
Slik går det når a vokser,,,
Oppgave 7
a)
Pytagoras:
$(R+r)^2 = R^2 + (2R-r)^2 \\ R^2+ 2Rr + r^2 = R^2 + 4R^2 - 4Rr +r^2 \\ 6Rr = 4R^2 \\ r = \frac 23R$
b)
Arealet av det grå (blå) feltet er arealet av kvartsirkelen minus arealene av de to halvsirklene.
$A = \frac{\pi(2R)^2}{4} - \frac{\pi R^2}{2} -\frac{\pi( \frac{2R}{3})^2}{2} \\ A = \pi R^2- \frac{9 \pi R^2}{18} - \frac{4 \pi R^2}{18} \\ A = \frac{5 \pi R^2}{18}$