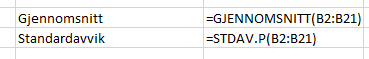2P 2017 høst LØSNING: Forskjell mellom sideversjoner
| (65 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://www.matematikk.net/matteprat/download/file.php?id=1800 Oppgaven som pdf] | [http://www.matematikk.net/matteprat/download/file.php?id=1800 Oppgaven som pdf] | ||
[http://www.matematikk.net/matteprat/download/file.php?id=1814 Løsningsforslag laget av mattepratbruker LektorNilsen] | |||
[http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=46524#p218927 Fasit laget av mattepratbruker Zain Mushtaq] | |||
Dersom du har en fasit eller et løsningsforslag som du ønsker å dele, så kan du sende det til cosinus@matematikk.net så legger vi det ut her. | Dersom du har en fasit eller et løsningsforslag som du ønsker å dele, så kan du sende det til cosinus@matematikk.net så legger vi det ut her. | ||
| Linje 8: | Linje 12: | ||
===Oppgave 1=== | ===Oppgave 1=== | ||
===a)=== | |||
Det var 15 elever som fikk en eller to, av totalt 60 elever. Det utgjør: | |||
$\frac{15}{60} \cdot 100$% = 25% | |||
===b)=== | |||
Medianelevene er elev nr. 30 og 31. Begge disse ligger i gruppen som fikk karakter 3, derfor er median = 3. | |||
===c)=== | |||
Multipliserer respektive karakterer med tilsvarende antall elever, summerer og deler på 60: | |||
$\frac{3+24+75+48+30+12}{60} = \frac{192}{60} = 3,2$ | |||
===Oppgave 2=== | ===Oppgave 2=== | ||
$3,54 \cdot 10^6 + 60000 = \\ 3540000 + 60000 = \\ 3600000 = 3,6 \cdot 10^6$ | |||
===Oppgave 3=== | ===Oppgave 3=== | ||
| Linje 27: | Linje 50: | ||
Fra A til stopp: Toget beveger seg 20 km på 20 minutter. Det vil si 60km på 60 minutter, altså en fart på 60 km/h. | Fra A til stopp: Toget beveger seg 20 km på 20 minutter. Det vil si 60km på 60 minutter, altså en fart på 60 km/h. | ||
Fra stopp til B: Toget beveger seg 60 km på 40 minutter. Det vil si 90 km på 60 minutter, altså en fart på 90 km/h. | Fra stopp til B: Toget beveger seg 60 km på 40 minutter. Det vil si 90 km på 60 minutter, altså en fart på 90 km/h (på 20 min er forflyttningen 30 km, det gjør det lettere). | ||
===Oppgave 4=== | ===Oppgave 4=== | ||
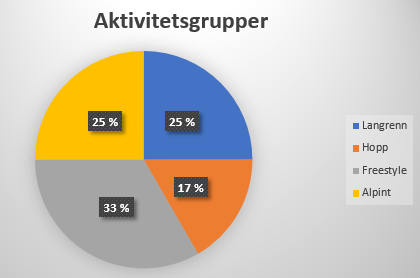
En sirkel er $ 360^{\circ} $. Det er totalt 240 medlemmer. | |||
Gradetall langrenn: $ \frac{60}{240} \cdot 360^{\circ} = 90^{\circ} $ | |||
Gradetall hopp: $ \frac{40}{240} \cdot 360^{\circ} = 60^{\circ} $ | |||
Gradetall freestyle: $ \frac{80}{240} \cdot 360^{\circ} = 120^{\circ} $ | |||
Gradetall alpint er som langrenn. | |||
[[File:2p-h17-1-4.png]] | |||
Siden dette er del 1, trenger du ikke prosentandelene i sektordiagrammet, men det er viktig å få godt fram hvor mange grader hver av sirkelsektorene er. | |||
===Oppgave 5=== | ===Oppgave 5=== | ||
120 kroner utgjør 40%. Finner hva 1% er og ganger med 100: | |||
$\frac{120}{40} \cdot 100 = 300$ | |||
Biletten kostet 300 kroner uten rabatt. | |||
===Oppgave 6 === | ===Oppgave 6 === | ||
===a)=== | |||
[[File:2p.h17-6a.png]] | |||
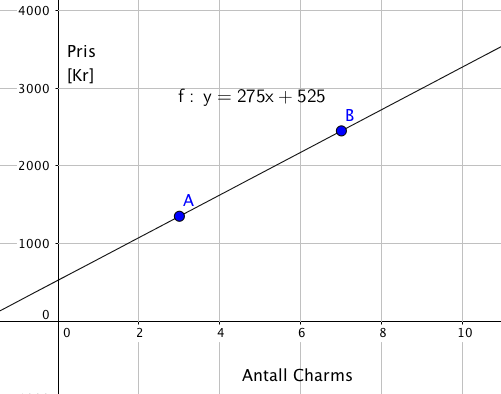
Ved å tegne punktene nøyaktig i et koordinatsystem kan det være mulig å komme i nærheten av et resultat, men det er ikke lett. Derfor er det trolig best å gjøre det ved regning. | |||
Likningen for en rett linje er | |||
y = ax + b | |||
$a = \frac{\Delta y}{\Delta y } = \frac{2450 - 1250}{7-3} = \frac{1100}{4} = 275$ | |||
Vi kan bruke punktet (3, 1350) og får | |||
$y = ax + b \\ 1350 = 275 \cdot 3 + b \\ b = 1350 - 825 \\ b = 525$ | |||
Vi får da y = 275x + 525 | |||
Armbåndet koster kr. 525,- og en charms koster kr. 275,- | |||
===b)=== | |||
Se a: y = 275x + 525 | |||
===c)=== | |||
$y= 274x + 525 \\ 3825 = 275x + 525 \\ 275x = 3825- 525 \\ 275x = 3300 \\ x = 12$ | |||
Hun har 12 charmes på armbåndet. | |||
===Oppgave 7=== | ===Oppgave 7=== | ||
| Linje 55: | Linje 130: | ||
$3 \cdot 20^2 +4 \cdot 20 = 1200 + 80 = 1280$ | $3 \cdot 20^2 +4 \cdot 20 = 1200 + 80 = 1280$ | ||
==DEL TO== | |||
===Oppgave 1=== | |||
===a)=== | |||
[[File:2p-h17-2-1abc.png]] | |||
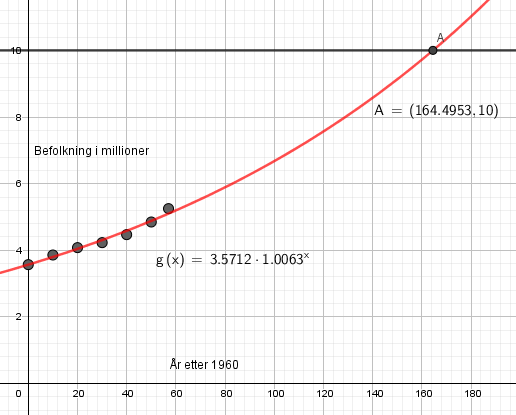
Vi bruker regresjon på Geogebra og ser at tallene passer godt med modellen. | |||
===b)=== | |||
1,006 forteller at befolkningsøkningen er på 0,6% per år. | |||
===c)=== | |||
Se bilde i a) | |||
===Oppgave 2=== | |||
===a)=== | |||
[[File:2p-h17-21ab.png]] | |||
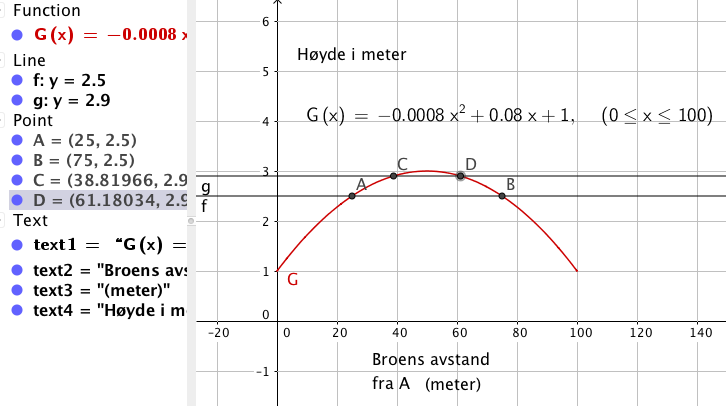
Se figur. | |||
===b)=== | |||
Ja, dersom man holder seg mellom 40 - 60 meter fra A | |||
===c)=== | |||
Det er 50 (75 - 25) meter i luftlinje, horisontalt. Se figur i a. | |||
===Oppgave 3=== | |||
===a)=== | |||
[[File:2p-h17-2-3a.png]] | |||
[[File:2p-h17-2-3ab.png]] | |||
Standardavviket er 10,25 og gjennomsnittet er 501,7. | |||
===b)=== | |||
Mindre standardavvik betyr mindre spredning i målepunktene. Maskin B fyller dermed flaskene mye jevnere enn maskin A. | |||
===Oppgave 4=== | |||
===a)=== | |||
[[File:2p-h17-2-4abc.png]] | |||
En lineær modell avtar med et gitt antall og i dette tilfellet er den g(x) = -12x + 280 | |||
===b)=== | |||
Dersom noe avtar med en gitt prosent per periode er endringen eksponentiell, I dette tilfellet $h(x)= 280 \cdot 0,91^x$ | |||
===c)=== | |||
y-verdien til A og B er henholdsvis 87 og 136. Dersom det etter ett år er 96 individer igjen ligger dette nærmest den eksponentielle modellen. | |||
===Oppgave 5=== | |||
===a)=== | |||
{| width="auto" | |||
|Ant. minutter | |||
|Ant. elever | |||
|Kumulativ frekvens | |||
|Relativ frekvens | |||
|Kumulativ relativ frekvens | |||
|- | |||
| [ 0, 60> | |||
| 3 | |||
| 3 | |||
| $\frac{3}{30} = 0,1 = 10$ % | |||
| 10% | |||
|- | |||
| [ 60, 180> | |||
|6 | |||
| 9 | |||
|$\frac{6}{30} = 0,2= 20$ % | |||
| 30% | |||
|- | |||
|| [ 180, 300> | |||
| 12 | |||
| 21 | |||
|$\frac{12}{30} = 0,4= 40$ % | |||
| 70% | |||
|- | |||
| [ 300, 420> | |||
| 6 | |||
| 27 | |||
|$\frac{6}{30} = 0,2= 20$ % | |||
| 90% | |||
|- | |||
| [ 420, 540> | |||
|3 | |||
| 30 | |||
|$\frac{3}{30} = 0,1= 10$ % | |||
| 100% | |||
|- | |||
|} | |||
===b)=== | |||
[[File:2p-h17-2-5b.png]] | |||
===c)=== | |||
Gjennomsnitt: | |||
$\frac {30 \cdot 3 + 120 \cdot 6 + 240 \cdot 12 + 360 \cdot 6 + 480 \cdot 3}{30} = 243$ minutter. | |||
===d)=== | |||
Det er 30 elever. Median personene vil være nr. 15 og 16, som begge ligger i intervallet 180 - 300 minutter. Det er totalt 9 elever i de to foregående intervaller, vi er derfor ute etter person 6 og 7 i dette intervallet. Dersom man forutsetter at elevene fordeler seg jevnt over intervallet øker treningsmengden med 10 minutter per elev ( klassebredde delt på antall (120:12)). De personene vi er ute etter trener altså 230 og 240 minutter i uken. Median er da ca 235 minutter per uke. | |||
==Oppgave 6== | |||
===a)=== | |||
Terminbeløp = avdrag + renter + gebyrer | |||
$2500 + \frac{90000 \cdot 0,4}{100} + 50 = 2910$ kr. | |||
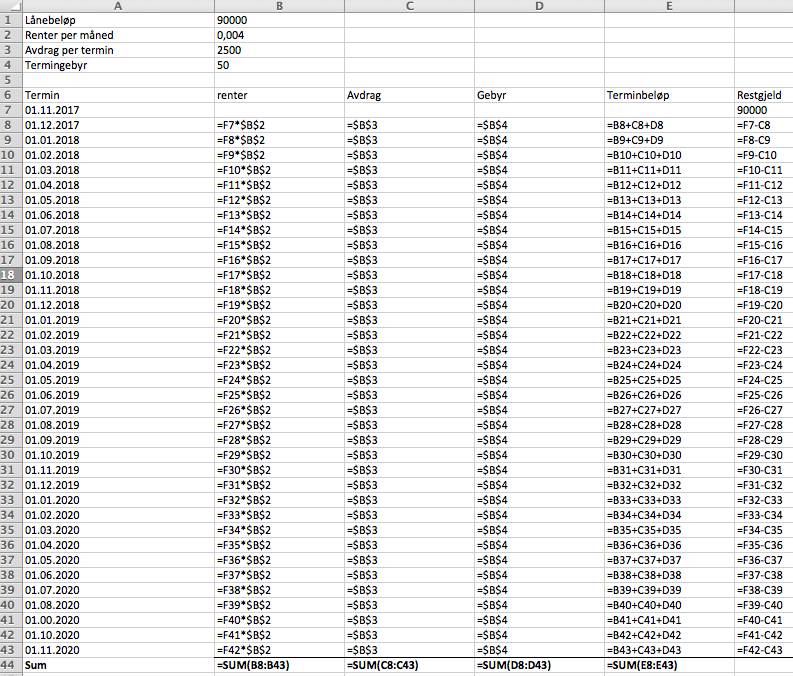
===b)=== | |||
[[File:2p-h17-2-6b1.png]] | |||
[[File:2p-h17-2-6b2.png]] | |||
===c)=== | |||
Lånet kostet renter og gebyrer: 6660kr + 1800kr = 8460 kr. | |||
Hun betalte altså 98460 kr tilbake til banken. | |||
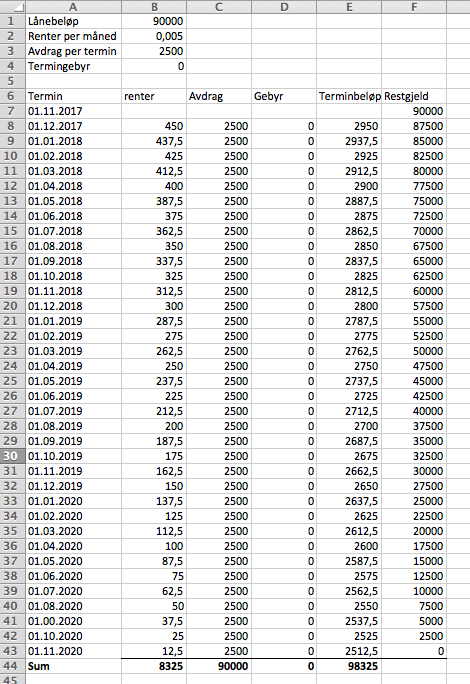
===d)=== | |||
[[File:2p-h17-2-6d.png]] | |||
Lånet ville kostet henne 8325 kr. Hun ville ha spart 135 kr. | |||
Siste sideversjon per 5. sep. 2018 kl. 18:54
Løsningsforslag laget av mattepratbruker LektorNilsen
Fasit laget av mattepratbruker Zain Mushtaq
Dersom du har en fasit eller et løsningsforslag som du ønsker å dele, så kan du sende det til cosinus@matematikk.net så legger vi det ut her.
DEL EN
Oppgave 1
a)
Det var 15 elever som fikk en eller to, av totalt 60 elever. Det utgjør:
$\frac{15}{60} \cdot 100$% = 25%
b)
Medianelevene er elev nr. 30 og 31. Begge disse ligger i gruppen som fikk karakter 3, derfor er median = 3.
c)
Multipliserer respektive karakterer med tilsvarende antall elever, summerer og deler på 60:
$\frac{3+24+75+48+30+12}{60} = \frac{192}{60} = 3,2$
Oppgave 2
$3,54 \cdot 10^6 + 60000 = \\ 3540000 + 60000 = \\ 3600000 = 3,6 \cdot 10^6$
Oppgave 3
a)
Toget drar fra A 13:40 og kommer til B 14:50, altså tar turen 1 time og 10 minutter.
b)
Toget stopper i 10 minutter.
c)
Fra A til stopp: Toget beveger seg 20 km på 20 minutter. Det vil si 60km på 60 minutter, altså en fart på 60 km/h.
Fra stopp til B: Toget beveger seg 60 km på 40 minutter. Det vil si 90 km på 60 minutter, altså en fart på 90 km/h (på 20 min er forflyttningen 30 km, det gjør det lettere).
Oppgave 4
En sirkel er $ 360^{\circ} $. Det er totalt 240 medlemmer.
Gradetall langrenn: $ \frac{60}{240} \cdot 360^{\circ} = 90^{\circ} $
Gradetall hopp: $ \frac{40}{240} \cdot 360^{\circ} = 60^{\circ} $
Gradetall freestyle: $ \frac{80}{240} \cdot 360^{\circ} = 120^{\circ} $
Gradetall alpint er som langrenn.
Siden dette er del 1, trenger du ikke prosentandelene i sektordiagrammet, men det er viktig å få godt fram hvor mange grader hver av sirkelsektorene er.
Oppgave 5
120 kroner utgjør 40%. Finner hva 1% er og ganger med 100:
$\frac{120}{40} \cdot 100 = 300$
Biletten kostet 300 kroner uten rabatt.
Oppgave 6
a)
Ved å tegne punktene nøyaktig i et koordinatsystem kan det være mulig å komme i nærheten av et resultat, men det er ikke lett. Derfor er det trolig best å gjøre det ved regning.
Likningen for en rett linje er
y = ax + b
$a = \frac{\Delta y}{\Delta y } = \frac{2450 - 1250}{7-3} = \frac{1100}{4} = 275$
Vi kan bruke punktet (3, 1350) og får
$y = ax + b \\ 1350 = 275 \cdot 3 + b \\ b = 1350 - 825 \\ b = 525$
Vi får da y = 275x + 525
Armbåndet koster kr. 525,- og en charms koster kr. 275,-
b)
Se a: y = 275x + 525
c)
$y= 274x + 525 \\ 3825 = 275x + 525 \\ 275x = 3825- 525 \\ 275x = 3300 \\ x = 12$
Hun har 12 charmes på armbåndet.
Oppgave 7
a)
Vi ser for oss en dyrekropp som består av hode + forbein + mage + bakbein + hale:
Figur fire: $4 \cdot 4 + 4 \cdot 5 + 4 + 4 \cdot 5 + 4 = 64$
b)
$n^2 + n(n+1) + n + n(n+1) + n = 3n^2+ 4n$
(hode + forbein + mage + bakbein + hale)
c)
Bruker formelen fra b og setter n = 20:
$3 \cdot 20^2 +4 \cdot 20 = 1200 + 80 = 1280$
DEL TO
Oppgave 1
a)
Vi bruker regresjon på Geogebra og ser at tallene passer godt med modellen.
b)
1,006 forteller at befolkningsøkningen er på 0,6% per år.
c)
Se bilde i a)
Oppgave 2
a)
Se figur.
b)
Ja, dersom man holder seg mellom 40 - 60 meter fra A
c)
Det er 50 (75 - 25) meter i luftlinje, horisontalt. Se figur i a.
Oppgave 3
a)
Standardavviket er 10,25 og gjennomsnittet er 501,7.
b)
Mindre standardavvik betyr mindre spredning i målepunktene. Maskin B fyller dermed flaskene mye jevnere enn maskin A.
Oppgave 4
a)
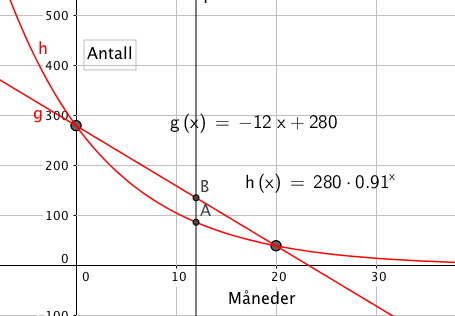
En lineær modell avtar med et gitt antall og i dette tilfellet er den g(x) = -12x + 280
b)
Dersom noe avtar med en gitt prosent per periode er endringen eksponentiell, I dette tilfellet $h(x)= 280 \cdot 0,91^x$
c)
y-verdien til A og B er henholdsvis 87 og 136. Dersom det etter ett år er 96 individer igjen ligger dette nærmest den eksponentielle modellen.
Oppgave 5
a)
| Ant. minutter | Ant. elever | Kumulativ frekvens | Relativ frekvens | Kumulativ relativ frekvens |
| [ 0, 60> | 3 | 3 | $\frac{3}{30} = 0,1 = 10$ % | 10% |
| [ 60, 180> | 6 | 9 | $\frac{6}{30} = 0,2= 20$ % | 30% |
| [ 180, 300> | 12 | 21 | $\frac{12}{30} = 0,4= 40$ % | 70% |
| [ 300, 420> | 6 | 27 | $\frac{6}{30} = 0,2= 20$ % | 90% |
| [ 420, 540> | 3 | 30 | $\frac{3}{30} = 0,1= 10$ % | 100% |
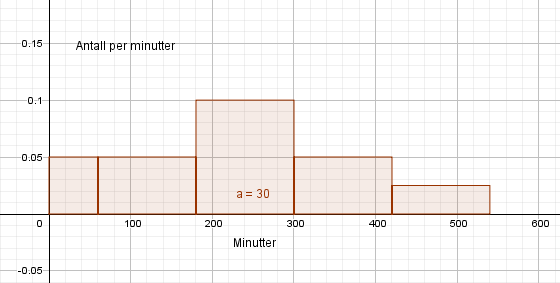
b)
c)
Gjennomsnitt:
$\frac {30 \cdot 3 + 120 \cdot 6 + 240 \cdot 12 + 360 \cdot 6 + 480 \cdot 3}{30} = 243$ minutter.
d)
Det er 30 elever. Median personene vil være nr. 15 og 16, som begge ligger i intervallet 180 - 300 minutter. Det er totalt 9 elever i de to foregående intervaller, vi er derfor ute etter person 6 og 7 i dette intervallet. Dersom man forutsetter at elevene fordeler seg jevnt over intervallet øker treningsmengden med 10 minutter per elev ( klassebredde delt på antall (120:12)). De personene vi er ute etter trener altså 230 og 240 minutter i uken. Median er da ca 235 minutter per uke.
Oppgave 6
a)
Terminbeløp = avdrag + renter + gebyrer
$2500 + \frac{90000 \cdot 0,4}{100} + 50 = 2910$ kr.
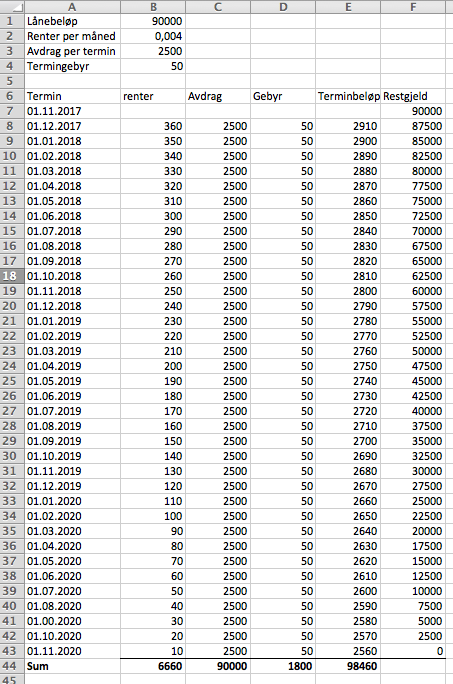
b)
c)
Lånet kostet renter og gebyrer: 6660kr + 1800kr = 8460 kr.
Hun betalte altså 98460 kr tilbake til banken.
d)
Lånet ville kostet henne 8325 kr. Hun ville ha spart 135 kr.