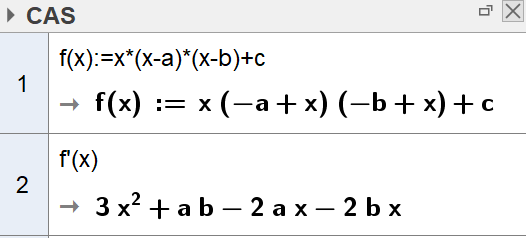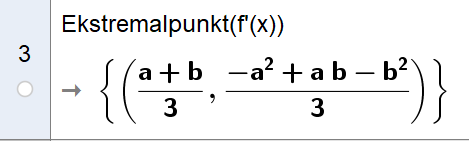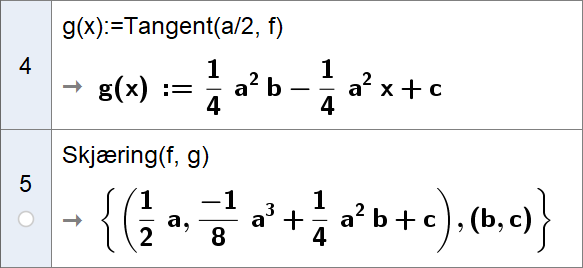1T 2020 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (35 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 3: | Linje 3: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=52377 Diskusjon av oppgaven på matteprat] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=52377 Diskusjon av oppgaven på matteprat] | ||
[https://matematikk.net/matteprat/download/file.php?id= | [https://matematikk.net/matteprat/download/file.php?id=3574 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | ||
[https://youtu.be/m4ModY4NIXs Videoløsningsforslag del 1 av Lektor Lainz] | |||
=DEL 1= | =DEL 1= | ||
| Linje 45: | Linje 47: | ||
Uttrykket er et fullstendig dersom: | Uttrykket er et fullstendig dersom: | ||
$k=2\cdot 2x \cdot \frac{1}{2} = | $kx=\pm 2\cdot 2x \cdot \frac{1}{2} \\ kx= \pm 2x \\ k = \pm 2$ | ||
==Oppgave 6== | |||
$\frac{5^{\frac{1}{2}} \cdot 4^{-1} \cdot 8^{\frac{2}{3}}}{\sqrt{20}\cdot 3^0} | |||
= \frac{\sqrt{5} \cdot (2^2)^{-1} \cdot (2^3)^{\frac{2}{3}}}{\sqrt{5} \cdot \sqrt{2} \cdot \sqrt{2} \cdot 1} | |||
= \frac{2^{-2} \cdot 2^2}{2} | |||
= \frac{1}{2}$ | |||
==Oppgave 7== | |||
$\frac{lg 1000 \cdot lg\frac{1}{10}}{lg 0,01 \cdot lg 10^{-\frac{1}{2}}} | |||
= \frac{3\cdot (-1)}{-2\cdot (-\frac{1}{2})} = \frac{-3}{1} = -3$ | |||
==Oppgave 8== | |||
===a)=== | |||
$\frac{2^{2+x}}{2^{1-2x}}=64 \\ 2^{2+x-(1-2x)} = 2^6 \\ 2^{2+x-1+2x} = 2^6 \\ 2^{3x+1}=2^6 \\ 3x+1 = 6 \\ x = \frac{6-1}{3} \\ x = \frac{5}{3} $ | |||
===b)=== | |||
$lg(\frac{1}{x^2-3x})=-1 \\ 10^{lg(\frac{1}{x^2-3x})}=10^{-1} \\ \frac{1}{x^2-3x} = \frac{1}{10} \\ x^2-3x = 10 \\ x^2-3x-10 = 0 \\ (x+2)(x-5)=0 \\ x = -2 \vee x = 5$ | |||
==Oppgave 9== | |||
- linjen $y=2x-4$ vil skjære y-aksen i x = -4, det samme som grafen til funksjonen $f$. | |||
- linjen $y=2x-4$ vil øke med 2 enheter på y-aksen for hver enhet på x-aksen. Dermed krysser den grafen til funksjonen $f$ i punktet (5,6). Du kan vise dette ved å tegne linjen og grafen til funksjonen f i samme koordinatsystem. | |||
- Grafen til funksjonen $f$ vil befinne seg under linjen $y = 2x-4$ når $x \in \langle 0,5 \rangle$ | |||
Vi har $f(x)<2x-4$ for $x \in \langle 0,5 \rangle$ | |||
==Oppgave 10== | |||
$f(x)=x^3+3x^2+3$ | |||
$f'(x)=3x^2+6x$ | |||
$f'(x)=-3 \\ 3x^2+6x = -3 \\ 3x^2+6x+3 = 0 \quad |:3 \\ x^2+2x+1=0 \\ (x+1)(x+1)=0 \\ x=-1$ | |||
Grafen til $f$ har bare én tangent med stigningstallet -3. | |||
Tangenten treffer funksjonen i punktet (-1, f(-1)). | |||
$f(-1)= (-1)^3+3(-1)^2+3 = -1+3+3 = 5$ | |||
Likning for tangenten: | |||
$y-y_1=a(x-x_1) \\ y-5 = -3(x-(-1)) \\ y -5 = -3x -3 \\ y = -3x+2$ | |||
==Oppgave 11== | |||
===a)=== | |||
$P(\overline{C} \cap \overline{G})=P(\overline{C})\cdot P(\overline{G})= \frac{8}{10}\cdot \frac{7}{9}=\frac{56}{90}=\frac{28}{45}$ | |||
Sannsynligheten for at verken Charlotte eller Gunnar blir trukket ut er $\frac{28}{45}$ | |||
===b)=== | |||
$P(C \cap G) = P(C)\cdot P(G) = \frac{2}{10} \cdot \frac{1}{9} = \frac{2}{90} = \frac{1}{45}$ | |||
Sannsynligheten for at det blir Charlotte og Gunnar som skal lage kampoppsettet er $\frac{1}{45}$ | |||
==Oppgave 12== | |||
===a)=== | |||
Bruker Pytagorassetningen til å finne lengden av BC: | |||
$CB^2=AB^2+AC^2 \\ CB = \sqrt{1^2+1^2} \\ CB=\sqrt{2}$ | |||
$\triangle ABC$ er likebeint, og $\angle A=90^{\circ}$. De to andre vinklene må derfor være $45^{\circ} .$ | |||
Finner $sin 45^{\circ}$: | |||
$ sin \angle ABC= \frac{AC}{BC} \\ sin 45^{\circ} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}\cdot 1}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}$ | |||
Finner $cos 45^{\circ}$: | |||
$ cos \angle ABC= \frac{AB}{BC} \\ cos 45^{\circ} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}\cdot 1}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}$ | |||
Vi har vist at $sin 45^{\circ} = cos 45^{\circ} = \frac{\sqrt{2}}{2}$ | |||
===b)=== | |||
Bruker arealsetningen. | |||
$A=\frac{1}{2}\cdot PQ\cdot PR \cdot sin \angle RPQ \\ A = \frac{1}{2}\cdot 6\sqrt{2}\cdot 8 \cdot sin 45^{\circ} = 3\cdot \sqrt{2}\cdot 8 \cdot \frac{\sqrt{2}}{2} = 24 \cdot \frac{2}{2} = 24$ | |||
Arealet av trekant $\triangle PQR$ er 24. | |||
===c)=== | |||
Brukes cosinussetningen: | |||
$QR^2 = PR ^2 + PQ^2 - 2\cdot PR\cdot PQ \cdot cos \angle RPQ$ | |||
$QR^2 = 8^2+(6\sqrt{2})^2 - 2\cdot 8 \cdot 6\sqrt{2}\cdot cos 45^{\circ}$ | |||
$QR^2 = 64 + 36\cdot 2 - 96 \cdot \sqrt{2}\cdot \frac{\sqrt{2}}{2}$ | |||
$QR^2 = 64+72 - 96 \cdot 1$ | |||
$QR^2 = 40$ | |||
$QR = \sqrt{40} = \sqrt{4\cdot 10} = \sqrt{4} \cdot \sqrt{10} = 2\sqrt{10}$ | |||
==Oppgave 13== | |||
Arealet av området er gitt ved $A=x\cdot y$. | |||
Antall meter gjerde er gitt ved $x+2y=1000$. Bruker denne likningen til å uttrykket y ved x: | |||
$x+2y=1000 \\ y=\frac{1000-x}{2} \\ y = -\frac{x}{2}+500$ | |||
Setter inn uttrykket for y i uttrykket for arealet: | |||
$A = x\cdot y \\ A=x\cdot (-\frac{x}{2}+500) \\ A=-\frac{1}{2}x^2+500x$ | |||
Arealet er nå gitt som en andregradsfunksjon med negativt andregradsledd. Funksjonen vil følgelig ha et toppunkt. Bruker derivasjon til å finne x-verdien til dette toppunktet: | |||
$A'(x) = -x+500$ | |||
Setter $A'(x)=0$ | |||
$-x+500 = 0 \\ x = 500$ | |||
Setter inn x=500 i uttrykket for y: | |||
$y=-\frac{500}{2}+500 = -250+500 = 250$ | |||
Arealet blir størst mulig når x = 500 meter og y = 250 meter. | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
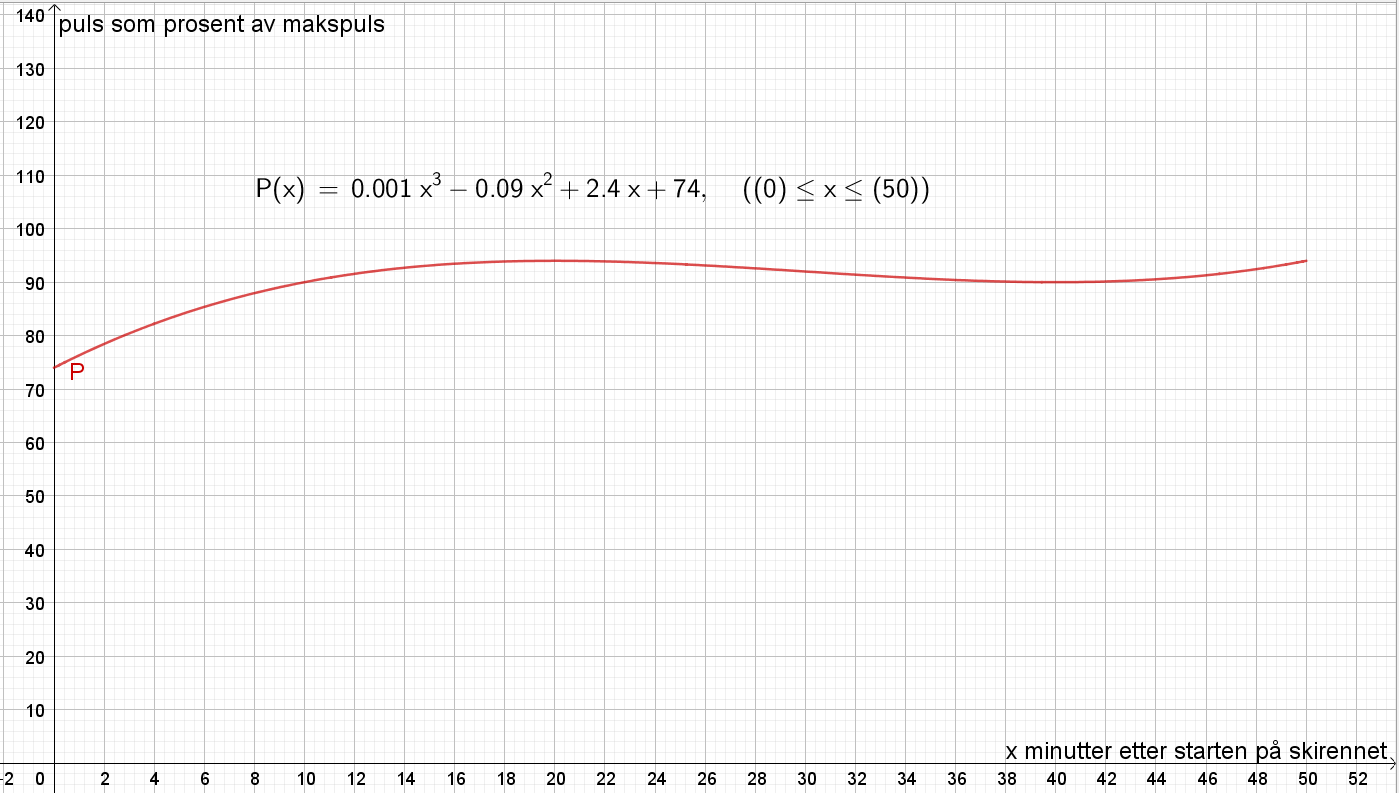
Bruker Geogebra til å tegne grafen til P. | |||
[[File: 1T_H20_del2_1a.png]] | |||
===b)=== | |||
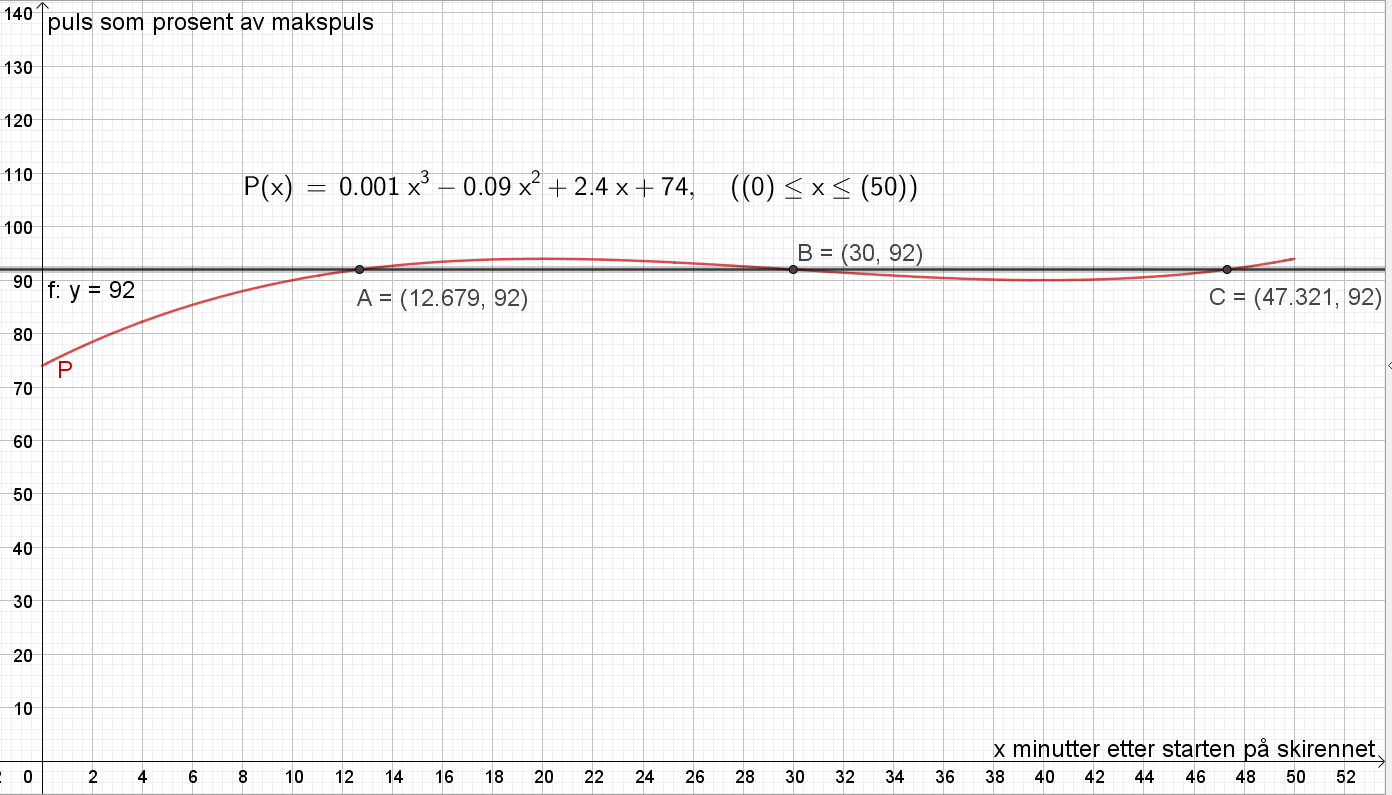
[[File: 1T_H20_del2_1b2.png]] | |||
Legger inn linja y = 92, og bruker "Skjæring mellom to objekt" for å finne skæringspunktene mellom denne linjen og grafen til $P$. Leser av x-verdien til skjæringspunktene A, B og C, og beregner antall minutter hvor Ole hadde høyere enn 92% av makspuls: | |||
$(30-12.7)+(50-47.3) = 20$ | |||
Pulsen til Ole høyere enn 92 % av makspuls i 20 minutter. | |||
===c)=== | |||
[[File: 1T_H20_del2_1c.png]] | |||
Den momentane vekstfarten til funksjonen $P$ når x = 5 er ca 1,575 % av makspuls per minutt. Det betyr at etter 5 minutter med skirenn, så øker pulsen til Ole med 1,575 % av makspulsen per minutt. | |||
==Oppgave 2== | |||
===a)=== | |||
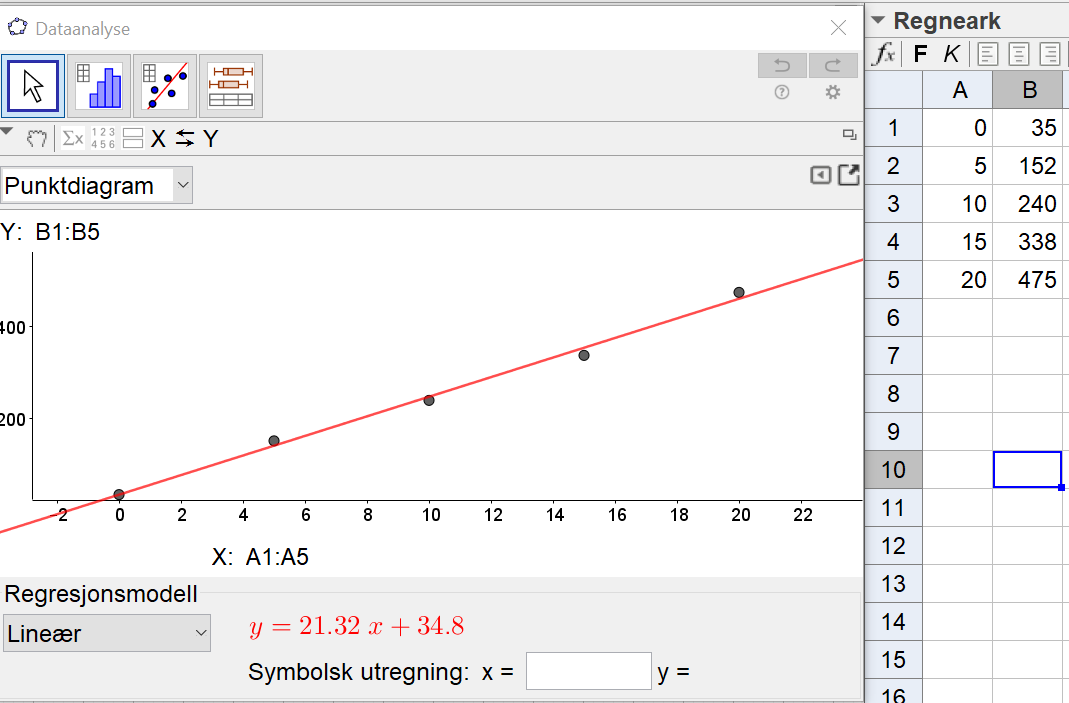
[[File: 1T_H20_del2_2a.png]] | |||
Bruker regresjonsanalyse i Geogebra. En lineær funksjon $M$ som kan beskrive utviklingen i perioden 2000–2020, er gitt ved $M(x)= 21,3x+34,8$, der x er antall år etter 2000. | |||
===b)=== | |||
Stigningstallet til funksjonen $M$, 21.3 forteller at antall personer som deltok i et mosjonsløp i årene 2000-2020 økte med gjennomsnittlig 21.3 personer per år. | |||
==Oppgave 3== | |||
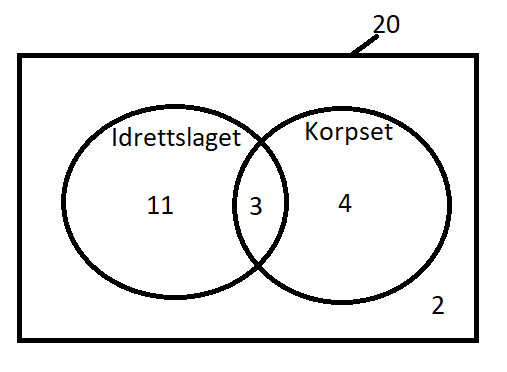
[[File: 1T_H20_del2_3.png]] | |||
$P(I\cap \overline{K}) = \frac{11}{20} = 55%$ | |||
Sannsynligheten for at eleven er med i idrettslaget, men ikke i korpset, er 55%. | |||
==Oppgave 4== | |||
===a)=== | |||
Bruker CAS i Geogebra til å bestemme $f'(x)$. | |||
[[File: 1T_H20_del2_4a.png]] | |||
===b)=== | |||
Den deriverte er et andregradsuttrykk med positivt andregradsledd. Den deriverte har derfor et bunnpunkt, som vi finner i CAS med kommandoen "Ekstremalpunkt": | |||
[[File: 1T_H20_del2_4b.png]] | |||
Bunnpunktet til den deriverte av f er der hvor y-verdien til den deriverte er mest negativ, og derfor der hvor grafen til f synker raskest. Dette skjer i $x=\frac{a+b}{3}=\frac{1}{3}(a+b)$, som skulle vises. | |||
===c)=== | |||
[[File: 1T_H20_del2_4c.png]] | |||
Linje 4 på CAS: finner ligning til tangenten g(x) til grafen til f i punktet $(\frac{a}{2}, f(\frac{a}{2}))$ | |||
Linje 5 på CAS: finner skjæringspunktene mellom grafen til f og tangenten g. De skjærer hverandre i tangeringspunktet $(\frac{a}{2}, f(\frac{a}{2}))$, og i punktet $(b,c)$, som skulle vises. | |||
==Oppgave 5== | |||
===a)=== | |||
Finner arealet av de to trekantene hver for seg med formelen $A=\frac{g\cdot h}{2}$, og legger arealene av de to trekantene sammen: | |||
$A=\frac{a\cdot h}{2}+\frac{b\cdot h}{2} = \frac{a\cdot h + b \cdot h}{2} = \frac{(a+b)\cdot h}{2}= \frac{a+b}{2}\cdot h$ | |||
===b)=== | |||
Finner arealet av de tre trekantene hver for seg med formelen $A=\frac{g\cdot h}{2}$, og legger arealene av de tre trekantene sammen: | |||
$A=\frac{\frac{a}{2}\cdot h}{2}+ \frac{\frac{a}{2}\cdot h}{2}+ \frac{b\cdot h}{2} = \frac{(\frac{a}{2}+\frac{a}{2}+b)\cdot h}{2}= \frac{a+b}{2}\cdot h$ | |||
===c)=== | |||
Et parallellogram er en figur hvor motstående sider er parallelle. Sidene er parvis like lange, og vinklene er parvis like store. Siden trapesene er kongruente, og de legges med samsvarende side mot hverandre slik at de like store vinklene er samsvarende, er side a+b og b+a parallelle. De to korte sidene til parallellogrammet har også like store samsvarende vinkler, og sidene er derfor parallelle. | |||
Bruker formelen for areal av et parallellogram, $A=g\cdot h$, og deler dette arealet på to, for å få arealet til et trapes. | |||
$A=\frac{(a+b)\cdot h}{2} = \frac{a+b}{2} \cdot h$ | |||
Siste sideversjon per 8. okt. 2021 kl. 07:12
Diskusjon av oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Videoløsningsforslag del 1 av Lektor Lainz
DEL 1
Oppgave 1
$y = 2x - 1$
Stigningstallet er 2 fordi y-verdien til funksjonen øker med 2 for hver gang x-verdien øker med 1. Konstantleddet er -1, der linjen krysser y-aksen.
Oppgave 2
$\frac{6,2\cdot10^4\cdot 2,5\cdot10^8}{0,0005} = \frac{6,2\cdot10^4\cdot2,5\cdot 10^8}{5\cdot10^{-4}} = 6,2\cdot 10^4 \cdot 0,5 \cdot 10^8\cdot 10^4 = 3,1 \cdot 10^{4+8+4} = 3,1\cdot 10^{16}$
Oppgave 3
$I. x+2y = 16 \\ II. 3x-y = 6$
Ganger likning II med 2, og legger sammen likning I og II.
$II. 3x - y = 6 \quad |\cdot 2 \\ II. 6x-2y = 12$
Likning I + II:
$ \quad\quad x+ 2y = 16 \\ + ( 6x - 2y = 12) \\ -------- \\ \quad\quad\quad\quad 7x = 28 \\ \quad\quad\quad\quad x = 4 $
Setter inn x = 4 i likning I:
$4+2y=16 \\ y = \frac{16-4}{2} \\ y=6$
Løsningen er x = 4 og y = 6. Du kan sjekke at det er riktig ved å sette inn disse verdiene i likning I og II, og se at likhetene stemmer.
Oppgave 4
$\frac{(x+y)^2-4xy}{x-y} = \frac{x^2+2xy+y^2-4xy}{x-y} = \frac{x^2-2xy+y^2}{x-y} =\frac{(x-y)^2}{x-y} = x-y$
Oppgave 5
$4x^2+kx+\frac{1}{4} = (2x)^2+kx+(\frac{1}{2})^2$
Uttrykket er et fullstendig dersom:
$kx=\pm 2\cdot 2x \cdot \frac{1}{2} \\ kx= \pm 2x \\ k = \pm 2$
Oppgave 6
$\frac{5^{\frac{1}{2}} \cdot 4^{-1} \cdot 8^{\frac{2}{3}}}{\sqrt{20}\cdot 3^0} = \frac{\sqrt{5} \cdot (2^2)^{-1} \cdot (2^3)^{\frac{2}{3}}}{\sqrt{5} \cdot \sqrt{2} \cdot \sqrt{2} \cdot 1} = \frac{2^{-2} \cdot 2^2}{2} = \frac{1}{2}$
Oppgave 7
$\frac{lg 1000 \cdot lg\frac{1}{10}}{lg 0,01 \cdot lg 10^{-\frac{1}{2}}} = \frac{3\cdot (-1)}{-2\cdot (-\frac{1}{2})} = \frac{-3}{1} = -3$
Oppgave 8
a)
$\frac{2^{2+x}}{2^{1-2x}}=64 \\ 2^{2+x-(1-2x)} = 2^6 \\ 2^{2+x-1+2x} = 2^6 \\ 2^{3x+1}=2^6 \\ 3x+1 = 6 \\ x = \frac{6-1}{3} \\ x = \frac{5}{3} $
b)
$lg(\frac{1}{x^2-3x})=-1 \\ 10^{lg(\frac{1}{x^2-3x})}=10^{-1} \\ \frac{1}{x^2-3x} = \frac{1}{10} \\ x^2-3x = 10 \\ x^2-3x-10 = 0 \\ (x+2)(x-5)=0 \\ x = -2 \vee x = 5$
Oppgave 9
- linjen $y=2x-4$ vil skjære y-aksen i x = -4, det samme som grafen til funksjonen $f$.
- linjen $y=2x-4$ vil øke med 2 enheter på y-aksen for hver enhet på x-aksen. Dermed krysser den grafen til funksjonen $f$ i punktet (5,6). Du kan vise dette ved å tegne linjen og grafen til funksjonen f i samme koordinatsystem.
- Grafen til funksjonen $f$ vil befinne seg under linjen $y = 2x-4$ når $x \in \langle 0,5 \rangle$
Vi har $f(x)<2x-4$ for $x \in \langle 0,5 \rangle$
Oppgave 10
$f(x)=x^3+3x^2+3$
$f'(x)=3x^2+6x$
$f'(x)=-3 \\ 3x^2+6x = -3 \\ 3x^2+6x+3 = 0 \quad |:3 \\ x^2+2x+1=0 \\ (x+1)(x+1)=0 \\ x=-1$
Grafen til $f$ har bare én tangent med stigningstallet -3.
Tangenten treffer funksjonen i punktet (-1, f(-1)).
$f(-1)= (-1)^3+3(-1)^2+3 = -1+3+3 = 5$
Likning for tangenten:
$y-y_1=a(x-x_1) \\ y-5 = -3(x-(-1)) \\ y -5 = -3x -3 \\ y = -3x+2$
Oppgave 11
a)
$P(\overline{C} \cap \overline{G})=P(\overline{C})\cdot P(\overline{G})= \frac{8}{10}\cdot \frac{7}{9}=\frac{56}{90}=\frac{28}{45}$
Sannsynligheten for at verken Charlotte eller Gunnar blir trukket ut er $\frac{28}{45}$
b)
$P(C \cap G) = P(C)\cdot P(G) = \frac{2}{10} \cdot \frac{1}{9} = \frac{2}{90} = \frac{1}{45}$
Sannsynligheten for at det blir Charlotte og Gunnar som skal lage kampoppsettet er $\frac{1}{45}$
Oppgave 12
a)
Bruker Pytagorassetningen til å finne lengden av BC:
$CB^2=AB^2+AC^2 \\ CB = \sqrt{1^2+1^2} \\ CB=\sqrt{2}$
$\triangle ABC$ er likebeint, og $\angle A=90^{\circ}$. De to andre vinklene må derfor være $45^{\circ} .$
Finner $sin 45^{\circ}$:
$ sin \angle ABC= \frac{AC}{BC} \\ sin 45^{\circ} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}\cdot 1}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}$
Finner $cos 45^{\circ}$:
$ cos \angle ABC= \frac{AB}{BC} \\ cos 45^{\circ} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}\cdot 1}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}$
Vi har vist at $sin 45^{\circ} = cos 45^{\circ} = \frac{\sqrt{2}}{2}$
b)
Bruker arealsetningen.
$A=\frac{1}{2}\cdot PQ\cdot PR \cdot sin \angle RPQ \\ A = \frac{1}{2}\cdot 6\sqrt{2}\cdot 8 \cdot sin 45^{\circ} = 3\cdot \sqrt{2}\cdot 8 \cdot \frac{\sqrt{2}}{2} = 24 \cdot \frac{2}{2} = 24$
Arealet av trekant $\triangle PQR$ er 24.
c)
Brukes cosinussetningen:
$QR^2 = PR ^2 + PQ^2 - 2\cdot PR\cdot PQ \cdot cos \angle RPQ$
$QR^2 = 8^2+(6\sqrt{2})^2 - 2\cdot 8 \cdot 6\sqrt{2}\cdot cos 45^{\circ}$
$QR^2 = 64 + 36\cdot 2 - 96 \cdot \sqrt{2}\cdot \frac{\sqrt{2}}{2}$
$QR^2 = 64+72 - 96 \cdot 1$
$QR^2 = 40$
$QR = \sqrt{40} = \sqrt{4\cdot 10} = \sqrt{4} \cdot \sqrt{10} = 2\sqrt{10}$
Oppgave 13
Arealet av området er gitt ved $A=x\cdot y$.
Antall meter gjerde er gitt ved $x+2y=1000$. Bruker denne likningen til å uttrykket y ved x:
$x+2y=1000 \\ y=\frac{1000-x}{2} \\ y = -\frac{x}{2}+500$
Setter inn uttrykket for y i uttrykket for arealet:
$A = x\cdot y \\ A=x\cdot (-\frac{x}{2}+500) \\ A=-\frac{1}{2}x^2+500x$
Arealet er nå gitt som en andregradsfunksjon med negativt andregradsledd. Funksjonen vil følgelig ha et toppunkt. Bruker derivasjon til å finne x-verdien til dette toppunktet:
$A'(x) = -x+500$
Setter $A'(x)=0$
$-x+500 = 0 \\ x = 500$
Setter inn x=500 i uttrykket for y:
$y=-\frac{500}{2}+500 = -250+500 = 250$
Arealet blir størst mulig når x = 500 meter og y = 250 meter.
DEL 2
Oppgave 1
a)
Bruker Geogebra til å tegne grafen til P.
b)
Legger inn linja y = 92, og bruker "Skjæring mellom to objekt" for å finne skæringspunktene mellom denne linjen og grafen til $P$. Leser av x-verdien til skjæringspunktene A, B og C, og beregner antall minutter hvor Ole hadde høyere enn 92% av makspuls:
$(30-12.7)+(50-47.3) = 20$
Pulsen til Ole høyere enn 92 % av makspuls i 20 minutter.
c)
Den momentane vekstfarten til funksjonen $P$ når x = 5 er ca 1,575 % av makspuls per minutt. Det betyr at etter 5 minutter med skirenn, så øker pulsen til Ole med 1,575 % av makspulsen per minutt.
Oppgave 2
a)
Bruker regresjonsanalyse i Geogebra. En lineær funksjon $M$ som kan beskrive utviklingen i perioden 2000–2020, er gitt ved $M(x)= 21,3x+34,8$, der x er antall år etter 2000.
b)
Stigningstallet til funksjonen $M$, 21.3 forteller at antall personer som deltok i et mosjonsløp i årene 2000-2020 økte med gjennomsnittlig 21.3 personer per år.
Oppgave 3
$P(I\cap \overline{K}) = \frac{11}{20} = 55%$
Sannsynligheten for at eleven er med i idrettslaget, men ikke i korpset, er 55%.
Oppgave 4
a)
Bruker CAS i Geogebra til å bestemme $f'(x)$.
b)
Den deriverte er et andregradsuttrykk med positivt andregradsledd. Den deriverte har derfor et bunnpunkt, som vi finner i CAS med kommandoen "Ekstremalpunkt":
Bunnpunktet til den deriverte av f er der hvor y-verdien til den deriverte er mest negativ, og derfor der hvor grafen til f synker raskest. Dette skjer i $x=\frac{a+b}{3}=\frac{1}{3}(a+b)$, som skulle vises.
c)
Linje 4 på CAS: finner ligning til tangenten g(x) til grafen til f i punktet $(\frac{a}{2}, f(\frac{a}{2}))$
Linje 5 på CAS: finner skjæringspunktene mellom grafen til f og tangenten g. De skjærer hverandre i tangeringspunktet $(\frac{a}{2}, f(\frac{a}{2}))$, og i punktet $(b,c)$, som skulle vises.
Oppgave 5
a)
Finner arealet av de to trekantene hver for seg med formelen $A=\frac{g\cdot h}{2}$, og legger arealene av de to trekantene sammen:
$A=\frac{a\cdot h}{2}+\frac{b\cdot h}{2} = \frac{a\cdot h + b \cdot h}{2} = \frac{(a+b)\cdot h}{2}= \frac{a+b}{2}\cdot h$
b)
Finner arealet av de tre trekantene hver for seg med formelen $A=\frac{g\cdot h}{2}$, og legger arealene av de tre trekantene sammen:
$A=\frac{\frac{a}{2}\cdot h}{2}+ \frac{\frac{a}{2}\cdot h}{2}+ \frac{b\cdot h}{2} = \frac{(\frac{a}{2}+\frac{a}{2}+b)\cdot h}{2}= \frac{a+b}{2}\cdot h$
c)
Et parallellogram er en figur hvor motstående sider er parallelle. Sidene er parvis like lange, og vinklene er parvis like store. Siden trapesene er kongruente, og de legges med samsvarende side mot hverandre slik at de like store vinklene er samsvarende, er side a+b og b+a parallelle. De to korte sidene til parallellogrammet har også like store samsvarende vinkler, og sidene er derfor parallelle.
Bruker formelen for areal av et parallellogram, $A=g\cdot h$, og deler dette arealet på to, for å få arealet til et trapes.
$A=\frac{(a+b)\cdot h}{2} = \frac{a+b}{2} \cdot h$