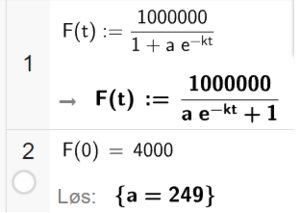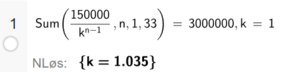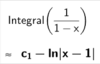S2 2025 vår LØSNING: Forskjell mellom sideversjoner
| (15 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 21: | Linje 21: | ||
$\int\frac{2x-1}{x^2-x-6}dx$ | $\int\frac{2x-1}{x^2-x-6}dx$ | ||
Bruker | Bruker integrasjon ved variabelskifte: | ||
$ | $u=x^2-x-6$ | ||
$2x-1 | $u'=2x-1$ | ||
$ | $u'=\frac{du}{dx} \Rightarrow dx = \frac{du}{u'}$ | ||
$-1= | $\int\frac{2x-1}{x^2-x-6}dx = \int\frac{u'}{u}dx=\int\frac{u'}{u}\frac{du}{u'} = \int \frac{1}{u}du = ln |u|+C = ln |x^2-x-6|+C$ | ||
Det er også mulig å bruke integrasjon ved delbrøkoppspalting. | |||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 110: | Linje 94: | ||
===a)=== | ===a)=== | ||
Rekken starter med tallet 2. For å finne neste tall, tar man forrige tall pluss forrige tall sitt figurnummer pluss 2. | Rekken starter med tallet 2. For å finne neste tall, tar man forrige tall pluss forrige tall sitt figurnummer pluss 2. Vi har $a_{n+1} = a_n+n+2 $ | ||
Når koden kjøres, skrives de 5 første tallene i rekken ut, nemlig 2, 5, 9, 14, 20. | Når koden kjøres, skrives de 5 første tallene i rekken ut, nemlig 2, 5, 9, 14, 20. | ||
| Linje 244: | Linje 228: | ||
* Det at flest nye husstander kjøper brannvarslingssystemet i uke 65, betyr at t=65 er vendepunktet. | * Det at flest nye husstander kjøper brannvarslingssystemet i uke 65, betyr at t=65 er vendepunktet. | ||
Generelt har vi at $F''(t)=0$ når $t=\frac{ln(a)}{k}$. | Generelt har vi at $F' '(t)=0$ når $t=\frac{ln(a)}{k}$. | ||
$65=\frac{ln(249)}{k}$ | $65=\frac{ln(249)}{k}$ | ||
| Linje 253: | Linje 237: | ||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
Summen av sparingen er en geometrisk rekke hvor ledd nr. n er gitt ved $a_n=a_1\cdot k^n$ | |||
Summen av de n første leddene i denne geometriske rekka er gitt ved: | |||
$S_n=a_1\cdot k\cdot\frac{k^n-1}{k-1}$ | |||
Her skal summen bli 3 750 000 kr, og k = 1,025. | |||
Her er to forskjellige måter å beregne $a_1$ i CAS: | |||
[[File: S2_V25_del2_4a.png|300px]] | |||
Nora må sette inn ca. 83 333 kr i banken hvert år for å nå målet. | |||
===b)=== | |||
Bruker at summen av nåverdiene til terminbeløpet, skal bli lik lånebeløpet: | |||
[[File: S2_V25_del2_4b2.png|300px]] | |||
Nora har regnet med at den årlige rentesatsen på lånet er 3,5 %. | |||
===c)=== | |||
[[File: S2_V25_del2_4c.png|300px]] | |||
Nora vil akkurat ikke nå målet sitt (men ikke langt unna). | |||
==Oppgave 5== | |||
For en uendelig geometrisk rekke gitt ved $1+x+x^2+x^3+...$ | |||
har vi at | |||
$\int 1\,dx + \int x\,dx + \int x^2\,dx + \int x^3\,dx + ... = \int \frac{1}{1-x} dx, \quad x\in \langle -1,1 \rangle$ | |||
Integrerer hvert ledd og får: | |||
$x+\frac{1}{2}x^2+\frac{1}{3}x^3+\frac{1}{4}x^4+...=-ln|x-1|$ | |||
Jeg har brukt CAS til å integrere $\frac{1}{1-x}$, og ignorerer integrasjonskonstanten, slik det står i oppgaven at vi kan gjøre. | |||
[[File: S2_V25_del2_5.png|100px]] | |||
Vi har rekken | |||
$\frac{1}{2^1}+\frac{1}{2}\cdot\frac{1}{2^2}+\frac{1}{3}\cdot\frac{1}{2^3}+\frac{1}{4}\cdot\frac{1}{2^4}+...$ | |||
som er den samme rekken som over, hvor $x=\frac{1}{2}$ | |||
Summen av denne rekken er altså | |||
$-ln|\frac{1}{2}-1|=-ln(\frac{1}{2})=-(ln\,1-ln\,2)=0+ln\,2=ln\,2$ | |||
Siste sideversjon per 3. aug. 2025 kl. 13:44
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
a)
$\int_{0}^{1} (2e^x+2x^2)dx$
$=[2e^x+\frac{2}{3}x^3]_{0}^{1}$
$=2e+\frac{2}{3}-2$
$=2e-\frac{4}{3}$
b)
$\int\frac{2x-1}{x^2-x-6}dx$
Bruker integrasjon ved variabelskifte:
$u=x^2-x-6$
$u'=2x-1$
$u'=\frac{du}{dx} \Rightarrow dx = \frac{du}{u'}$
$\int\frac{2x-1}{x^2-x-6}dx = \int\frac{u'}{u}dx=\int\frac{u'}{u}\frac{du}{u'} = \int \frac{1}{u}du = ln |u|+C = ln |x^2-x-6|+C$
Det er også mulig å bruke integrasjon ved delbrøkoppspalting.
Oppgave 2
Vi har at
- $f'(x)=-\frac{2}{x^3}$
- $\int_{1}^{2}f(x)dx=\frac{11}{14}$
Integrerer f'(x) for å få et uttrykk for f(x):
$f(x)=\int -\frac{2}{x^3} dx = -2\int x^{-3}dx=\frac{-2}{-2}x^{-2} +C=\frac{1}{x^2}+C$
Bruker det bestemte integralet som likning for å finne C:
$\int_{1}^{2}(\frac{1}{x^2}+C )\, dx=\frac{11}{14}$
$[-\frac{1}{x}+Cx]_{1}^{2}=\frac{11}{14}$
$-\frac{1}{2}+2C-(-1+C)=\frac{11}{14}$
$C+\frac{1}{2}=\frac{11}{14}$
$C=\frac{11}{14}-\frac{7}{14}$
$C=\frac{4}{14}=\frac{2}{7}$
Vi har:
$f(x)=\frac{1}{x^2}+\frac{2}{7}$
Oppgave 3
a)
| k | 1 | 2 | 3 | 6 |
|---|---|---|---|---|
| $P(X=k)$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{2}$ |
$E(x)=\frac{1+2+3+6+6+6}{6}=\frac{24}{6}=4$
b)
$Var(x)=\frac{(1-4)^2+(2-4)^2+(3-4)^2+3\cdot(6-4)^2}{6}$
$=\frac{9+4+1+12}{6}=\frac{26}{6}=\frac{13}{3}$
Oppgave 4
a)
Rekken starter med tallet 2. For å finne neste tall, tar man forrige tall pluss forrige tall sitt figurnummer pluss 2. Vi har $a_{n+1} = a_n+n+2 $
Når koden kjøres, skrives de 5 første tallene i rekken ut, nemlig 2, 5, 9, 14, 20.
b)
Eleven ønsker å finne summen av de 5 første tallene i rekken. Resultatet som skrives ut blir 50.
Oppgave 5
a)
Grensekostnaden til 180 enheter er 138 kroner. Dette er stigningstallet til tangenten til K når x=180, og forteller derfor om hvor mye kostnaden stiger per enhet i det punktet (momentan vekstfart).
Enhetskostnaden er kostnaden per enhet. Når det blir produsert 180 enheter, koster det 14920 kroner. Det betyr at kostnaden per enhet er $\frac{14920}{180}=82,89$ kr per enhet. Jeg vet hva svaret blir, fordi det er stigningstallet til den rette linjen som går gjennom origo og punktet (180, 14920).
b)
Vi har $I(x)=p\cdot x$
Ønsker å finne p slik at $O'(180)=0$
$O'(x)= I'(x)-K'(x)= p-K'(x)$
$O'(180)=0$
$p-K'(180)=0$
$p-138=0$
$p=138$
Prisen må være 138 kroner per enhet for å få størst mulig overskudd ved produksjon og salg av 180 enheter. Vi legger merke til at prisen er den samme som grensekostnaden for produksjon av 180 enheter.
Oppgave 6
a)
$H_0: \mu=20\,km/L$
$H_1: \mu>20\,km/L$
b)
$z=\frac{\bar{x}-\mu_0}{\sigma / \sqrt{n}}=\frac{21-20}{2,5/\sqrt{25}}=\frac{1}{2,5/5}=\frac{1}{1/2}=2$
Bruker vedlegget med standard normalfordeling og leser av tabellen at:
$P(Z\leq 2)=0,9772$
Det er mer enn 95 % sannsynlig, så Benz A/S kan si at bensinen øker kjørelengden.
DEL 2
Oppgave 1
a)
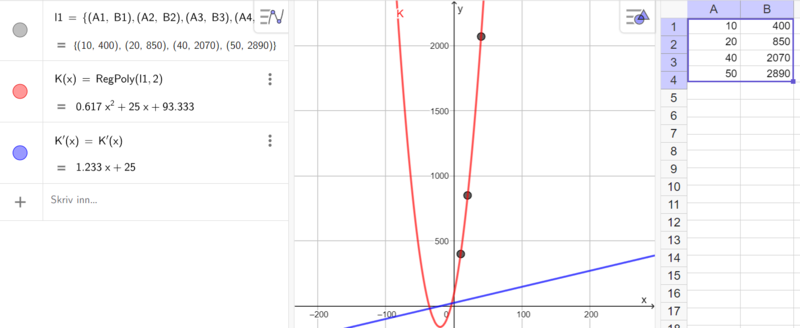
Utfører en regresjonsanalyse i Geogebra ut fra dataene i tabellen. Velger en andregradspolynom og får et uttrykk for K(x). Deriverer så K(x) i Geogebra, og viser at K'(x)=1,23x+25.
b)
I'(35)=85,7. Dette er grenseinntekten ved salg av 35 enheter, og forteller oss at å øke salget med én enhet ville økt inntekten med 85,7 kroner.
K'(35)=68,2. Dette er grensekostnaden ved salg av 35 enheter, og forteller oss at å øke salget med én enhet ville økt kostnaden med 68,2 kroner.
Det vil altså lønne seg å øke produksjonen til 36 enheter.
c)
Svaret på 558 forteller oss at samlet kostnad for å øke produksjonen fra 20 til 30 enheter er 558 kroner.
Dette virker som en unødvendig komplisert måte å finne ut av det på, da det enkleste ville vært å regne ut K(30)-K(20).
Oppgave 2
a)
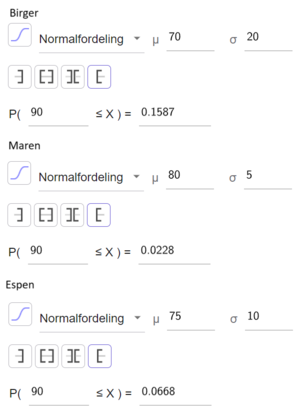
Bruker sannsynlighetskalkulatoren i Geogebra.
Sannsynligheten for at Birger hopper lenger enn 90 meter i et tilfeldig hopp er 0,1587. For Maren er sannsynligheten 0,0228, og for Espen er den 0,0668.
b)
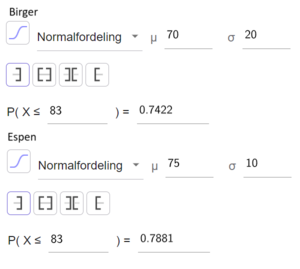
Finner sannsynligheten for at Birger og Espen hver for seg hopper kortere enn 83 meter:
Sannsynligheten for at begge hopper kortere enn 83 meter (og at Maren dermed hopper lengst) er $0,7422\cdot 0,7881=0,5849$
c)
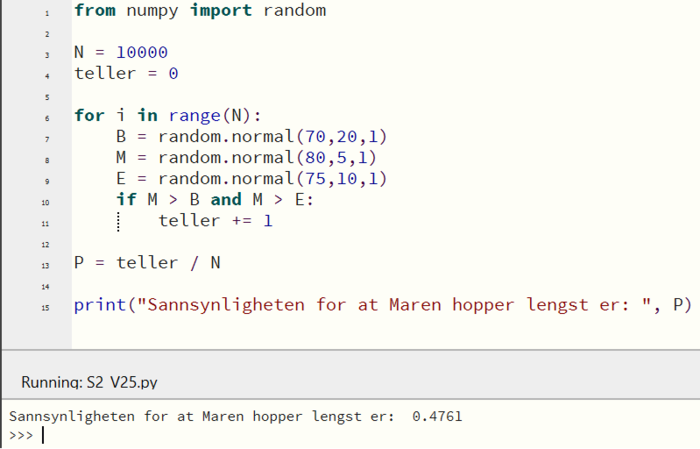
Lager en simulering i Python:
Sannsynligheten for at Maren hopper lengst i denne omgangen er omtrent 0,476.
Oppgave 3
a)
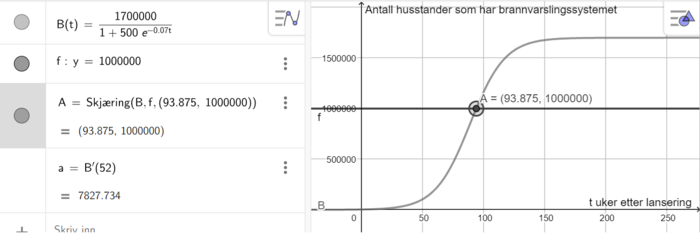
Tegner grafen til B i Geogebra, og finner skjæringspunktet med linja y = 1 000 000 (se punkt A). Det tar nesten 94 uker før halvparten av husstandene i byen har brannvarslingssystemet.
b)
$B'(52)=7827,7$ (se algebrafeltet på skjermbildet i oppgave a).
Det bestyr at 52 uker etter lansering, øker antall husstander som har brannvarslingssystemet med ca. 7828 husstander per uke.
c)
En logistisk modell er gitt ved:
$F(t)=\frac{N}{1+a\cdot e^{-kt}}$
- N = 1 000 000, det maksimale antall husstander som får brannvarslingssystemet.
- Bruker CAS i Geogebra til å finne $a$:
- Det at flest nye husstander kjøper brannvarslingssystemet i uke 65, betyr at t=65 er vendepunktet.
Generelt har vi at $F' '(t)=0$ når $t=\frac{ln(a)}{k}$.
$65=\frac{ln(249)}{k}$
$k=0,085$
- Modellen er gitt ved $F(t)=\frac{1000000}{1+249\cdot e^{-0,085t}}$
Oppgave 4
a)
Summen av sparingen er en geometrisk rekke hvor ledd nr. n er gitt ved $a_n=a_1\cdot k^n$
Summen av de n første leddene i denne geometriske rekka er gitt ved:
$S_n=a_1\cdot k\cdot\frac{k^n-1}{k-1}$
Her skal summen bli 3 750 000 kr, og k = 1,025.
Her er to forskjellige måter å beregne $a_1$ i CAS:
Nora må sette inn ca. 83 333 kr i banken hvert år for å nå målet.
b)
Bruker at summen av nåverdiene til terminbeløpet, skal bli lik lånebeløpet:
Nora har regnet med at den årlige rentesatsen på lånet er 3,5 %.
c)
Nora vil akkurat ikke nå målet sitt (men ikke langt unna).
Oppgave 5
For en uendelig geometrisk rekke gitt ved $1+x+x^2+x^3+...$
har vi at
$\int 1\,dx + \int x\,dx + \int x^2\,dx + \int x^3\,dx + ... = \int \frac{1}{1-x} dx, \quad x\in \langle -1,1 \rangle$
Integrerer hvert ledd og får:
$x+\frac{1}{2}x^2+\frac{1}{3}x^3+\frac{1}{4}x^4+...=-ln|x-1|$
Jeg har brukt CAS til å integrere $\frac{1}{1-x}$, og ignorerer integrasjonskonstanten, slik det står i oppgaven at vi kan gjøre.
Vi har rekken
$\frac{1}{2^1}+\frac{1}{2}\cdot\frac{1}{2^2}+\frac{1}{3}\cdot\frac{1}{2^3}+\frac{1}{4}\cdot\frac{1}{2^4}+...$
som er den samme rekken som over, hvor $x=\frac{1}{2}$
Summen av denne rekken er altså
$-ln|\frac{1}{2}-1|=-ln(\frac{1}{2})=-(ln\,1-ln\,2)=0+ln\,2=ln\,2$