2P 2025 Høst LØSNING: Forskjell mellom sideversjoner
| (39 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 34: | Linje 34: | ||
====a)==== | |||
Det er 20 vogner i pariserhjulet. Fra tabellen ser man at det er 15 vogner med folk i, altså 5 tomme. | |||
====b)==== | |||
0, 0, 0, 0, 0, 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4 | |||
Median : 2,5 Summen av de to midterste tallene (2 +3), delt på to. | |||
Gjennomsnitt: $\frac{4 \cdot 6 + 3 \cdot 4 + 2 \cdot 3 + 2}{20} = \frac{44}{20} = 2,2$ | |||
====c)==== | |||
Den kumulative frekvensen for to personer i hver vogn er summen av vogner med to personer eller mindre, altså 3 + 2 + 5 = 10 vogner. Det er 10 vogner med to personer eller færre. | |||
===Oppgave 5=== | ===Oppgave 5=== | ||
Hypotenusen i trekanten blir $h = \sqrt{8^2 + 6^2} = \sqrt{100} = 10$ | |||
Radius i sirkelen blir da 5 cm. Opphøyd i andre blir det $25cm^2$ som ganget med pi, 3,14 blir større enn $75cm^2$. | |||
===Oppgave 6=== | ===Oppgave 6=== | ||
Vi får tre likninger med tre ukjente: | |||
Pris: | |||
Sukkerspinn = x, popcorn = y og softis = x | |||
'''1''' Eva: x + y = 90 | |||
'''2''' Trine: y + z = 80 | |||
'''3''' Magnus: x + z = 70 | |||
'''3:''' x = 70- z inn i '''1:''' (70 - z) + y = 90 | |||
Løser '''2''' for y: y =80 - z , setter inn for 1 på linje fire og får: | |||
70- z + 80 - z = 90 | |||
-2z = -60 | |||
z = 30 | |||
Da blir x = 40 og y = 50 | |||
Sukkerspinn koster 40 kroner, popkorn 50 kroner og softis 30 kroner. | |||
===Oppgave 7=== | ===Oppgave 7=== | ||
====a)==== | |||
Serielån har like store avdrag hele låneperioden. hun må betale 50000 kroner i årlig avdrag. | |||
====b)==== | |||
Det første terminbeløpet: | |||
renten av 400000 pluss avdraget: $\quad \frac{400000\cdot 5}{100} kr + 50000kr = 20000kr+50000kr = 70000$ | |||
Det andre terminbeløpet: Nå er det rentebærende beløpet 350000kr | |||
$ \frac{350000 \cdot 5}{100}kr + 50000kr = 17500kr + 50000kr = 67500 kr$ | |||
====c)==== | |||
Dersom nedbetalingstiden kortes ned til 5år blir avdrag per termin 80 000 kr. Rentebærende beløp før 3 termin blir 240000; | |||
Rentekostnader: $\frac{240000 \cdot 5}{100}kr = 12000 kr $ | |||
===Oppgave 8=== | |||
Planen til Johann er å sette arven i banken, 1,5 millioner kroner. Hvert år skal han ta ut 120 000 kr. Dette gjør han så lenge det er 120 000 kr eller mer igjen på konto. Han regner med at renten er på 5,6 % i perioden. | |||
Programmet printer ut beløpet som står på konto. Linje 7 legger til renten og trekke fra uttaket. Linje 8 legget til ett år her runde løkken kjøres. | |||
== DEL TO == | == DEL TO == | ||
===Oppgave 1=== | ===Oppgave 1=== | ||
====a)==== | |||
[[File:09022026-02.png|centre|600px]] | |||
====b)==== | |||
Økningen er på 12,4% i følge modellen. | |||
====c)==== | |||
Det tar nesten 2 år. i januar 27, i følge modellen. | |||
====d)==== | |||
[[File:09022026-04.png|centre|400px]] | |||
Satte inn en glider for vekstfaktor b. en månedlig omsetningsøkning på mellom 47 -58% vil føre til passering av 20 000kr i løpet av desember. I følge modellen | |||
===Oppgave 2=== | ===Oppgave 2=== | ||
| Linje 52: | Linje 138: | ||
Fatima : $ | Fatima : $100000kr\cdot1,36 = 136 000kr$ | ||
Adrian: $100000kr \cdot 1,057^5 = 100000kr \cdot 1,319 = 131900kr$ | |||
Vegard: $100000kr \cdot 1,2 \cdot 0,89 \cdot 0,9 \cdot 1,23 \cdot 1,17= 100000kr \cdot 1,267 = 126700kr$ | |||
===Oppgave 5=== | ===Oppgave 5=== | ||
====a)==== | |||
Det bor 923 personer i Åseral kommune. | |||
'''Median verdi:''' | |||
For å finne hvilke klasse medianverdien ligger i trengs det ingen forutsetninger. Medianverdien vil være gjennomsnittsalderen til person nr. 461 og 462. Dersom vi legger sammen antallet i de to første klassene ser man at det blir 535, altså ligger median ett sted i aldersgruppen 18 til 50 år. Dersom man ønsker å bestemme verdien mer nøyaktig må man forutsette at '''fordelingen er tilnærmet jevn i intervallet.''' | |||
Det er 31 forskjellige aldere representert i intervallet, fra og med 18, til og med 49. Det gir ca. 11,2 personer på hver alder. Vi vet at person 461,5 har medianverdien. Vi trekker fra 188 som er antall personer i første intervall: 461,5 - 188 =273,5. | |||
Vi må altså 273,5 personen "inn" i det andre intervallet og det går ca. 11,2 personer på hvert år. Det betyr at vi skal 24,5 år inn i intervallet som starter med 18 år. Det gir oss en alder på 18år + 24,5år = 42.5år. Det betyr at medianalderen i Åseral trolig ligger i området 42- 43 år. | |||
'''Gjennomsnittsalder''' | |||
Vi antar at adersdordelingen gruperer seg rundt klassemidpunktet. Altå at gjennomsnittsalderen i første intervall er 9 år ((18-0)/2), I andre intervall blir kassemidpunkt 34 år (50-18)/2 + 18 osv. Dette vet vi ikke. Det er en '''antakelse'''. Vi multipliserer antallet i hvert intervall med klassemitdpunktet for å finne den tottale alder i hvert intervall. | |||
====b)==== | |||
====c)==== | |||
===Oppgave 6=== | ===Oppgave 6=== | ||
| Linje 67: | Linje 177: | ||
De trenger 1,125 kubikkmeter med grus. | De trenger 1,125 kubikkmeter med grus. | ||
====b)==== | ====b)==== | ||
Volum kjegle: | |||
$\frac 13 \pi r^2 \cdot h = \frac{\pi \cdot 1,25^2 \cdot 1}{3}m^3 =1,56 m^3$ | |||
De fikk nok grus. | |||
Siste sideversjon per 9. feb. 2026 kl. 08:17
DEL EN
Oppgave 1
En prosent av 300 er 3. En økning på 15 fra 300 er 5%
$\frac{15kr \cdot 100}{300} = 5$%
Prisen går opp med 5%
Oppgave 2
$\frac{x}{90}= \frac{400}{120}$
$120x = 36000$
$x=300$
I 2022 kostet varen 300kr. dersom den fulgte indeksen.
Oppgave 3
$\frac{x}{33000} = \frac{1}{1100}$
$11x =330$
$x = 10$
Modellen er 30 cm. høy.
Oppgave 4
a)
Det er 20 vogner i pariserhjulet. Fra tabellen ser man at det er 15 vogner med folk i, altså 5 tomme.
b)
0, 0, 0, 0, 0, 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4
Median : 2,5 Summen av de to midterste tallene (2 +3), delt på to.
Gjennomsnitt: $\frac{4 \cdot 6 + 3 \cdot 4 + 2 \cdot 3 + 2}{20} = \frac{44}{20} = 2,2$
c)
Den kumulative frekvensen for to personer i hver vogn er summen av vogner med to personer eller mindre, altså 3 + 2 + 5 = 10 vogner. Det er 10 vogner med to personer eller færre.
Oppgave 5
Hypotenusen i trekanten blir $h = \sqrt{8^2 + 6^2} = \sqrt{100} = 10$
Radius i sirkelen blir da 5 cm. Opphøyd i andre blir det $25cm^2$ som ganget med pi, 3,14 blir større enn $75cm^2$.
Oppgave 6
Vi får tre likninger med tre ukjente:
Pris:
Sukkerspinn = x, popcorn = y og softis = x
1 Eva: x + y = 90
2 Trine: y + z = 80
3 Magnus: x + z = 70
3: x = 70- z inn i 1: (70 - z) + y = 90
Løser 2 for y: y =80 - z , setter inn for 1 på linje fire og får:
70- z + 80 - z = 90
-2z = -60 z = 30 Da blir x = 40 og y = 50
Sukkerspinn koster 40 kroner, popkorn 50 kroner og softis 30 kroner.
Oppgave 7
a)
Serielån har like store avdrag hele låneperioden. hun må betale 50000 kroner i årlig avdrag.
b)
Det første terminbeløpet:
renten av 400000 pluss avdraget: $\quad \frac{400000\cdot 5}{100} kr + 50000kr = 20000kr+50000kr = 70000$
Det andre terminbeløpet: Nå er det rentebærende beløpet 350000kr
$ \frac{350000 \cdot 5}{100}kr + 50000kr = 17500kr + 50000kr = 67500 kr$
c)
Dersom nedbetalingstiden kortes ned til 5år blir avdrag per termin 80 000 kr. Rentebærende beløp før 3 termin blir 240000;
Rentekostnader: $\frac{240000 \cdot 5}{100}kr = 12000 kr $
Oppgave 8
Planen til Johann er å sette arven i banken, 1,5 millioner kroner. Hvert år skal han ta ut 120 000 kr. Dette gjør han så lenge det er 120 000 kr eller mer igjen på konto. Han regner med at renten er på 5,6 % i perioden.
Programmet printer ut beløpet som står på konto. Linje 7 legger til renten og trekke fra uttaket. Linje 8 legget til ett år her runde løkken kjøres.
DEL TO
Oppgave 1
a)
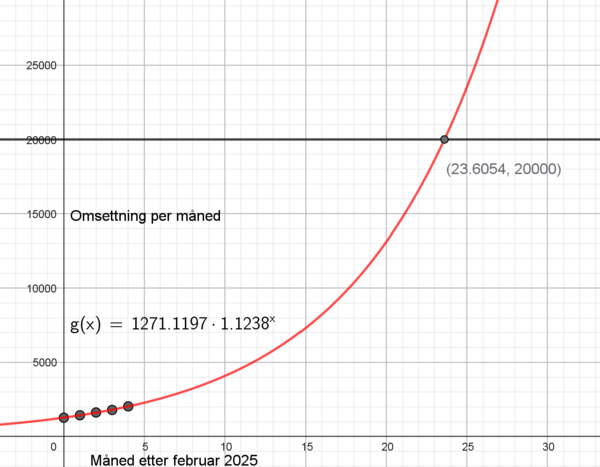
b)
Økningen er på 12,4% i følge modellen.
c)
Det tar nesten 2 år. i januar 27, i følge modellen.
d)
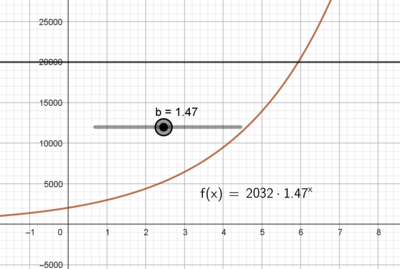
Satte inn en glider for vekstfaktor b. en månedlig omsetningsøkning på mellom 47 -58% vil føre til passering av 20 000kr i løpet av desember. I følge modellen
Oppgave 2
Oppgave 3
Oppgave 4
Fatima : $100000kr\cdot1,36 = 136 000kr$
Adrian: $100000kr \cdot 1,057^5 = 100000kr \cdot 1,319 = 131900kr$
Vegard: $100000kr \cdot 1,2 \cdot 0,89 \cdot 0,9 \cdot 1,23 \cdot 1,17= 100000kr \cdot 1,267 = 126700kr$
Oppgave 5
a)
Det bor 923 personer i Åseral kommune.
Median verdi:
For å finne hvilke klasse medianverdien ligger i trengs det ingen forutsetninger. Medianverdien vil være gjennomsnittsalderen til person nr. 461 og 462. Dersom vi legger sammen antallet i de to første klassene ser man at det blir 535, altså ligger median ett sted i aldersgruppen 18 til 50 år. Dersom man ønsker å bestemme verdien mer nøyaktig må man forutsette at fordelingen er tilnærmet jevn i intervallet.
Det er 31 forskjellige aldere representert i intervallet, fra og med 18, til og med 49. Det gir ca. 11,2 personer på hver alder. Vi vet at person 461,5 har medianverdien. Vi trekker fra 188 som er antall personer i første intervall: 461,5 - 188 =273,5.
Vi må altså 273,5 personen "inn" i det andre intervallet og det går ca. 11,2 personer på hvert år. Det betyr at vi skal 24,5 år inn i intervallet som starter med 18 år. Det gir oss en alder på 18år + 24,5år = 42.5år. Det betyr at medianalderen i Åseral trolig ligger i området 42- 43 år.
Gjennomsnittsalder
Vi antar at adersdordelingen gruperer seg rundt klassemidpunktet. Altå at gjennomsnittsalderen i første intervall er 9 år ((18-0)/2), I andre intervall blir kassemidpunkt 34 år (50-18)/2 + 18 osv. Dette vet vi ikke. Det er en antakelse. Vi multipliserer antallet i hvert intervall med klassemitdpunktet for å finne den tottale alder i hvert intervall.
b)
c)
Oppgave 6
a)
De trenger $V = lbh = 25m \cdot 0,60 m \cdot 0,075 m =1, 125m^3$
De trenger 1,125 kubikkmeter med grus.
b)
Volum kjegle:
$\frac 13 \pi r^2 \cdot h = \frac{\pi \cdot 1,25^2 \cdot 1}{3}m^3 =1,56 m^3$
De fikk nok grus.