R1 2010 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (59 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
===Alternative løsninger=== | |||
[http://www.matematikk.net/matteprat/download/file.php?id=992 Løsning fra Udir] | |||
[http://ndla.no/nb/node/108297?fag=57933 Løsning fra NDLA] | |||
== Del 1 == | == Del 1 == | ||
| Linje 8: | Linje 12: | ||
== a) == | == a) == | ||
1)<p></p> | 1)<p></p> | ||
< | <math>f(x)=2xe^x \\f'(x) = 2e^x+2xe^x = 2(1+x)e^x</math> | ||
<p></p> | <p></p> | ||
2)<p></p> | 2)<p></p> | ||
< | <math>g(x) = 3\sqrt{x^2-1}\\ \text{setter u lik x i andre minus en og bruker kjerneregelen} \\ g'(x) = (\frac{3}{2\sqrt{x^2-1}}) \cdot (2x) = \frac {3x}{\sqrt{x^2-1}}</math> | ||
== b) == | == b) == | ||
< | <math>P(x) = 2x^3-6x^2-2x+6 \\ P(1) = 2 \cdot 1^3- 6 \cdot 1^2 -2 \cdot1 + 6 = 0 \\ (2x^3-6x^2-2x+6 ):(x-1) =2x^2-4x-6 \\ -(2x^3-2x^2) \\ \quad \quad\quad -4x^2-2x \\ \quad \quad \quad-(-4x^2+4x) \\\quad \quad\quad \quad\quad \quad\quad \quad \quad -6x+6 \\\quad \quad\quad \quad\quad \quad\quad \quad -(-6x+6) \\\quad \quad \quad \quad\quad \quad\quad \quad\quad \quad \quad \quad\quad\quad0 </math> | ||
$(x-1) \cdot (2x^2-4x-6) = 0 \\ x = 1 \vee x = \frac{-(-2) \pm \sqrt {4+12}}{2} \\ x= -1 \vee x = 1 \vee x = 3$ | |||
== c) == | == c) == | ||
1)<p></p> | 1)<p></p> | ||
[[Fil: | [[Fil:1c-r1-h2010.png]]<p></p> | ||
2)<p></p> | 2)<p></p> | ||
< | <math>\vec v (t) = \vec r'(t) = [6,-10t] \\\vec v (1) = [6,-10] </math> | ||
Farten v har retning langs tangenten i A. | |||
<p></p> | <p></p> | ||
3)<p></p> | 3)<p></p> | ||
< | <math>\vec a (t) = \vec v'(t) = [0,-10] </math> <p></p>Akslerasjonen i x rettning er null. Akslerasjonen i y rettning er konstant lik 10, nedover. | ||
== d) == | == d) == | ||
Det er to muligheter for en av hver: Gutt,jente eller jente,gutt: | |||
<p></p> | |||
<math>\frac{6}{10} \cdot \frac{4}{9} +\frac{4}{10} \cdot \frac{6}{9} = \frac{8}{15}</math> | |||
<p></p> | |||
Man observerer at dette er en hypergeometrisk situasjon og får samme resultat ved å bruke den formelen. | |||
== e) == | == e) == | ||
[[Fil:Konstruksjon2.png]] | |||
1. Avsetter AB lik 10cm. | |||
2. Konstruerer vinkel A 60 + 15 grader er 75 grader. | |||
3. Trekker linjen gjennom A. C ligger ett eller annet sted på denne linjen. | |||
4. Nedfeller normalen fra B på linjen i pkt. 3 og vi har funnet C. | |||
== f) == | == f) == | ||
1)<p></p> | 1)<p></p> | ||
< | <math>\lim_{x \to 2}\frac{x^2+4}{x-2}</math> <p></p>Når x går mot to går brøken mot pluss eller minus uendelig (avhengig fra hvilken side man nærmer seg to) og grensen eksisterer ikke. | ||
<p></p> | <p></p> | ||
2)<p></p> | 2)<p></p> | ||
< | <math> \lim_{x \to 2} \frac{x^2-4}{x-2}= \lim_{x \to 2} \frac{(x+2)(x-2)}{x-2}=\lim_{x \to 2}(x+2) = 4 </math> | ||
== Oppgave 2 == | == Oppgave 2 == | ||
| Linje 44: | Linje 66: | ||
== a) == | == a) == | ||
< | <math>x^2+r^2 = (r+y)^2 \\ x^2+r^2 = r^2+2ry + y^2 \\ x^2 = 2ry +y^2 = y(y+2r)</math> | ||
== b) == | == b) == | ||
< | <math>\angle CTS = 30^{\circ} \Rightarrow \angle TSC = 120^{\circ} \Rightarrow \angle AST = 60^{\circ}</math> | ||
<p></p> | <p></p> | ||
Trekanten ATS er en 30, 60 , 90 trekant hvilket betyr at det korteste katetet er halvparten av hypotenusens lengde. Korteste katet har lengden r og hypotenuseen har lengde r+y, hvilket betyr at y = r. | Trekanten ATS er en 30, 60 , 90 trekant hvilket betyr at det korteste katetet er halvparten av hypotenusens lengde. Korteste katet har lengden r og hypotenuseen har lengde r+y, hvilket betyr at y = r. | ||
=DEL TO= | |||
== Oppgave 3: == | == Oppgave 3: == | ||
| Linje 59: | Linje 82: | ||
== a) == | == a) == | ||
< | <math>f(x) = 4x^2 \cdot e^{-x} \\ f'(x) = 4 \cdot 2 \cdot x \cdot e^{-x} + 4x^2 \cdot e^{-x} \cdot (-1) \\ f'(x) = 8xe^{-x} - 4x^2e^{-x}</math><p></p> | ||
Grafen til den deriverte:<p></p> | Grafen til den deriverte:<p></p> | ||
[[Fil:2010høsta3.png]] | [[Fil:2010høsta3.png]] | ||
| Linje 65: | Linje 88: | ||
== b) == | == b) == | ||
f har ekstremalpunkter for x = 0 og for x = 2 | f har ekstremalpunkter for x = 0 og for x = 2 | ||
<p></p> | |||
f' er negativ når x er mindre enn null og positiv når x er større enn null. x = 0 gir da et minimumspunkt. f' er positiv for når x er mindre enn to og negativ for verdier større enn 2. x = 2 gir et maksimumspunkt.<p></p> | |||
Minimum: (0,f(0)) = (0,0)<p></p> | |||
Maksimum: <math>(2,f(2))=(2,\frac{16}{e^2})</math> | |||
<p></p> | |||
Man observere at grafen til den deriverte har to ekstremalpunkter. Den dobbelderiverte er null i disse punktene og det er vendepunkter. x verdiene for disse er:<p></p> | |||
x = 0,59 og x = 3,41<p></p> | |||
For å finne y verdien setter vi inn i funksjonsuttrykket for f:<p></p> | |||
Vendepunkter: | |||
(0,57, f(0,57)) og (3,41, f(3,41)) som gir punktene (0,57 , 0,76) og (3,41 , 1,53). | |||
== Oppgave 4 == | |||
== a) == | |||
Trekant ABP:<math> A= \frac{a \cdot h}{2}</math> <p></p> | |||
Trekant PCD:<math> A= \frac{a \cdot (a-h)}{2} = \frac{a^2 - ah}{2}</math> | |||
== b) == | |||
Summen av arealene:<p></p> | |||
$\frac{a \cdot h}{2} + \frac{a^2 - ah}{2} = \frac{a^2}{2}$<p></p> | |||
Dette er halvparten av kvadratets areal, uavhengig av hvor i kvadratet P måtte befinne seg. | |||
== Oppgave 5 == | |||
== a) == | |||
<math>\vec{AB}= [7-(-1),-2-0] = [8,-2] \\ \vec{AC} = [3-(-1),6-0]=[4,6]</math> | |||
<p></p> | |||
Vinkel A:<p></p> | |||
$ \vec{AB} \cdot \vec{AC} = | \vec{AB} | \cdot | \vec{AC} | \cdot cos \alpha \\ | |||
cos \alpha = \frac { \vec{AB} \cdot \vec{AC}} {| \vec{AB}| \cdot| \vec{AC}|} \\ | |||
cos \alpha = \frac{[8,-2] \cdot [4,6]}{ \sqrt{8^2+(-2)^2} \cdot \sqrt{4^2+6^2}} = \frac{32-12}{ \sqrt{68} \cdot \sqrt{52}} = \frac{20}{ \sqrt{16 \cdot 17 \cdot 13}} \\ | |||
\alpha = 78,4^{\circ}$ | |||
== b) == | |||
<math>\vec{DE} = - \frac 34\vec{AB} +\frac 34 \vec{AC} = - \frac 34[8,-2] +\frac 34 [4,6] = [-3,6] </math><p></p> | |||
<math>\vec{BC} = [-4,8]\\\vec{BC}=k\vec{DE} </math><p></p> | |||
dvs. vektorene er parallelle. | |||
== c) == | |||
== d) == | |||
== e) == | |||
== Oppgave 6 == | |||
== Alternativ 1 == | |||
== a) == | |||
<math>AC = \sqrt{2^2 + 2^2 } = \sqrt{8} \\ AG = \sqrt{8+2^2} = \sqrt {12}</math> | |||
== b) == | |||
Bruker Pytagoras og ser at strekningen S er summen av hypotenusene i trekantene APE og PFG. | |||
== c) == | |||
[[Fil:R1høst20106.png]] | |||
Når x = 1 er veien kortest, S er da kvadratroten av tyve. Figuren over viser S og S'. | |||
== d) == | |||
== Alternativ 2 == | |||
== a) == | |||
== b) == | |||
== c) == | |||
== d) == | |||
== Oppgave 7 == | |||
== a) == | |||
<math> | |||
y = \frac{-a}{\sqrt{9-a^2}}x + \frac{9}{\sqrt{9-a^2}} \\A:\quad \quad y = 0 \\ \frac{-a}{\sqrt{9-a^2}}x + \frac{9}{\sqrt{9-a^2}} = 0 \\ x = \frac 9a \\ A:\quad\quad (\frac 9a, 0)\\ | |||
B:\quad\quad x=0 \\ y= \frac{9}{\sqrt{9-a^2}} \\ B:\quad\quad (0,\frac{9}{\sqrt{9-a^2}}) | |||
</math> | |||
== b) == | |||
<math>A = F(a) = \frac{gh}{2} = \frac{9}{a} \cdot \frac{9}{\sqrt{9-a^2}} \cdot \frac{1}{2}= \frac{81}{2a \sqrt{9-a^2}}</math> | |||
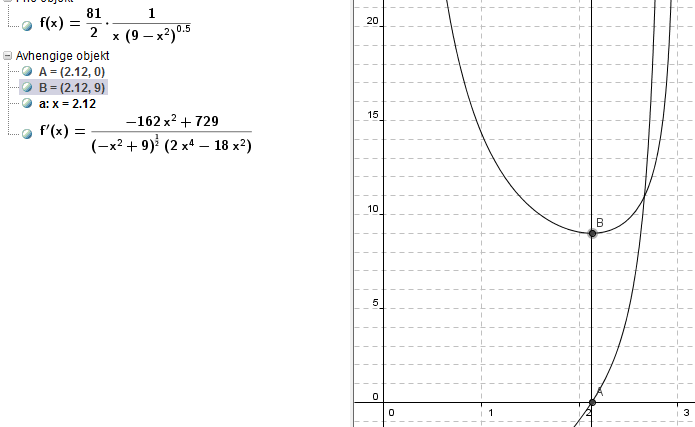
== c) og d) == | |||
[[Fil:Sstt.png]] | |||
Figuren viser F og F'. | |||
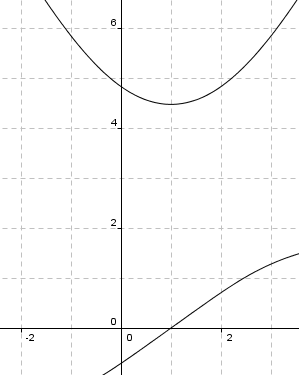
Trekanten har sin minste verdi når a = 2,12. | |||
== d) == | |||
Siste sideversjon per 18. mai 2016 kl. 14:16
Alternative løsninger
Del 1
Oppgave 1:
a)
1)
<math>f(x)=2xe^x \\f'(x) = 2e^x+2xe^x = 2(1+x)e^x</math>
2)
<math>g(x) = 3\sqrt{x^2-1}\\ \text{setter u lik x i andre minus en og bruker kjerneregelen} \\ g'(x) = (\frac{3}{2\sqrt{x^2-1}}) \cdot (2x) = \frac {3x}{\sqrt{x^2-1}}</math>
b)
<math>P(x) = 2x^3-6x^2-2x+6 \\ P(1) = 2 \cdot 1^3- 6 \cdot 1^2 -2 \cdot1 + 6 = 0 \\ (2x^3-6x^2-2x+6 ):(x-1) =2x^2-4x-6 \\ -(2x^3-2x^2) \\ \quad \quad\quad -4x^2-2x \\ \quad \quad \quad-(-4x^2+4x) \\\quad \quad\quad \quad\quad \quad\quad \quad \quad -6x+6 \\\quad \quad\quad \quad\quad \quad\quad \quad -(-6x+6) \\\quad \quad \quad \quad\quad \quad\quad \quad\quad \quad \quad \quad\quad\quad0 </math>
$(x-1) \cdot (2x^2-4x-6) = 0 \\ x = 1 \vee x = \frac{-(-2) \pm \sqrt {4+12}}{2} \\ x= -1 \vee x = 1 \vee x = 3$
c)
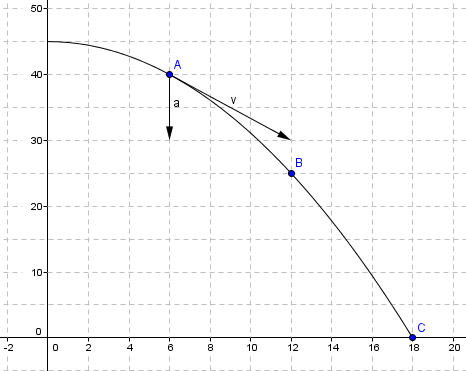
1)
2)
<math>\vec v (t) = \vec r'(t) = [6,-10t] \\\vec v (1) = [6,-10] </math>
Farten v har retning langs tangenten i A.
3)
<math>\vec a (t) = \vec v'(t) = [0,-10] </math>
Akslerasjonen i x rettning er null. Akslerasjonen i y rettning er konstant lik 10, nedover.
d)
Det er to muligheter for en av hver: Gutt,jente eller jente,gutt:
<math>\frac{6}{10} \cdot \frac{4}{9} +\frac{4}{10} \cdot \frac{6}{9} = \frac{8}{15}</math>
Man observerer at dette er en hypergeometrisk situasjon og får samme resultat ved å bruke den formelen.
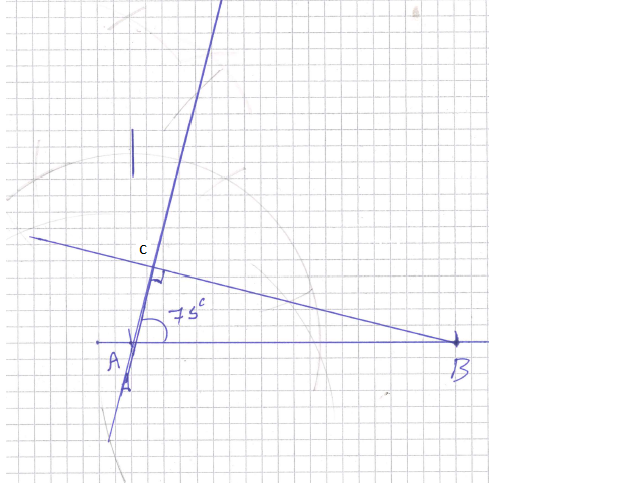
e)
1. Avsetter AB lik 10cm.
2. Konstruerer vinkel A 60 + 15 grader er 75 grader.
3. Trekker linjen gjennom A. C ligger ett eller annet sted på denne linjen.
4. Nedfeller normalen fra B på linjen i pkt. 3 og vi har funnet C.
f)
1)
<math>\lim_{x \to 2}\frac{x^2+4}{x-2}</math>
Når x går mot to går brøken mot pluss eller minus uendelig (avhengig fra hvilken side man nærmer seg to) og grensen eksisterer ikke.
2)
<math> \lim_{x \to 2} \frac{x^2-4}{x-2}= \lim_{x \to 2} \frac{(x+2)(x-2)}{x-2}=\lim_{x \to 2}(x+2) = 4 </math>
Oppgave 2
a)
<math>x^2+r^2 = (r+y)^2 \\ x^2+r^2 = r^2+2ry + y^2 \\ x^2 = 2ry +y^2 = y(y+2r)</math>
b)
<math>\angle CTS = 30^{\circ} \Rightarrow \angle TSC = 120^{\circ} \Rightarrow \angle AST = 60^{\circ}</math>
Trekanten ATS er en 30, 60 , 90 trekant hvilket betyr at det korteste katetet er halvparten av hypotenusens lengde. Korteste katet har lengden r og hypotenuseen har lengde r+y, hvilket betyr at y = r.
DEL TO
Oppgave 3:
a)
<math>f(x) = 4x^2 \cdot e^{-x} \\ f'(x) = 4 \cdot 2 \cdot x \cdot e^{-x} + 4x^2 \cdot e^{-x} \cdot (-1) \\ f'(x) = 8xe^{-x} - 4x^2e^{-x}</math>
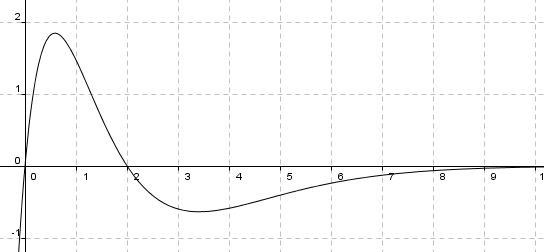
Grafen til den deriverte:
b)
f har ekstremalpunkter for x = 0 og for x = 2
f' er negativ når x er mindre enn null og positiv når x er større enn null. x = 0 gir da et minimumspunkt. f' er positiv for når x er mindre enn to og negativ for verdier større enn 2. x = 2 gir et maksimumspunkt.
Minimum: (0,f(0)) = (0,0)
Maksimum: <math>(2,f(2))=(2,\frac{16}{e^2})</math>
Man observere at grafen til den deriverte har to ekstremalpunkter. Den dobbelderiverte er null i disse punktene og det er vendepunkter. x verdiene for disse er:
x = 0,59 og x = 3,41
For å finne y verdien setter vi inn i funksjonsuttrykket for f:
Vendepunkter:
(0,57, f(0,57)) og (3,41, f(3,41)) som gir punktene (0,57 , 0,76) og (3,41 , 1,53).
Oppgave 4
a)
Trekant ABP:<math> A= \frac{a \cdot h}{2}</math>
Trekant PCD:<math> A= \frac{a \cdot (a-h)}{2} = \frac{a^2 - ah}{2}</math>
b)
Summen av arealene:
$\frac{a \cdot h}{2} + \frac{a^2 - ah}{2} = \frac{a^2}{2}$
Dette er halvparten av kvadratets areal, uavhengig av hvor i kvadratet P måtte befinne seg.
Oppgave 5
a)
<math>\vec{AB}= [7-(-1),-2-0] = [8,-2] \\ \vec{AC} = [3-(-1),6-0]=[4,6]</math>
Vinkel A:
$ \vec{AB} \cdot \vec{AC} = | \vec{AB} | \cdot | \vec{AC} | \cdot cos \alpha \\ cos \alpha = \frac { \vec{AB} \cdot \vec{AC}} {| \vec{AB}| \cdot| \vec{AC}|} \\ cos \alpha = \frac{[8,-2] \cdot [4,6]}{ \sqrt{8^2+(-2)^2} \cdot \sqrt{4^2+6^2}} = \frac{32-12}{ \sqrt{68} \cdot \sqrt{52}} = \frac{20}{ \sqrt{16 \cdot 17 \cdot 13}} \\ \alpha = 78,4^{\circ}$
b)
<math>\vec{DE} = - \frac 34\vec{AB} +\frac 34 \vec{AC} = - \frac 34[8,-2] +\frac 34 [4,6] = [-3,6] </math>
<math>\vec{BC} = [-4,8]\\\vec{BC}=k\vec{DE} </math>
dvs. vektorene er parallelle.
c)
d)
e)
Oppgave 6
Alternativ 1
a)
<math>AC = \sqrt{2^2 + 2^2 } = \sqrt{8} \\ AG = \sqrt{8+2^2} = \sqrt {12}</math>
b)
Bruker Pytagoras og ser at strekningen S er summen av hypotenusene i trekantene APE og PFG.
c)
Når x = 1 er veien kortest, S er da kvadratroten av tyve. Figuren over viser S og S'.
d)
Alternativ 2
a)
b)
c)
d)
Oppgave 7
a)
<math> y = \frac{-a}{\sqrt{9-a^2}}x + \frac{9}{\sqrt{9-a^2}} \\A:\quad \quad y = 0 \\ \frac{-a}{\sqrt{9-a^2}}x + \frac{9}{\sqrt{9-a^2}} = 0 \\ x = \frac 9a \\ A:\quad\quad (\frac 9a, 0)\\ B:\quad\quad x=0 \\ y= \frac{9}{\sqrt{9-a^2}} \\ B:\quad\quad (0,\frac{9}{\sqrt{9-a^2}}) </math>
b)
<math>A = F(a) = \frac{gh}{2} = \frac{9}{a} \cdot \frac{9}{\sqrt{9-a^2}} \cdot \frac{1}{2}= \frac{81}{2a \sqrt{9-a^2}}</math>
c) og d)
Trekanten har sin minste verdi når a = 2,12.