Bokstavuttrykk: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (70 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
== Innledning == | ==== Innledning ==== | ||
Det er ikke noe mystisk med bokstaver i et utrykk. En bokstav står for en spesiell tallverdi. | |||
[[File:24062025-01.png|centre|200px]] | |||
I linje to er det en rød firkant. Dersom likheten skal være riktig må verdien til firkanten være lik 1. I linje tre og fire er denne verdien byttet ut med bokstaver. For at linje 3 og 4 skal være riktige må både x og b ha verdien 1. | |||
Algebra, eller bokstavregning, viser generelle sammenhenger. Tallregning eller aritmetikk gir oss mer spesielle sammenhenger. | Algebra, eller bokstavregning, viser generelle sammenhenger. Tallregning eller aritmetikk gir oss mer spesielle sammenhenger. | ||
<br> | <br> | ||
En sirkel har radius 10 cm. Hva er arealet av sirkelen? | En sirkel har radius 10 cm. Hva er arealet av sirkelen? | ||
<br> | <br> | ||
Arealet blir:<br> | Arealet blir:<br> | ||
\[A = 10cm \cdot 10cm \cdot {\pi} =314,2 cm^2.\] | |||
<br> | <br> | ||
Men, det gjelder bare når radius i sirkelen er 10 cm. For alle andre radier er dette arealet feil. | Men, det gjelder bare når radius i sirkelen er 10 cm. For alle andre radier er dette arealet feil. | ||
| Linje 12: | Linje 18: | ||
Et areal som gjelder for en sirkel, uansett radius:<br> | Et areal som gjelder for en sirkel, uansett radius:<br> | ||
\[A = {\pi}r^2\] | |||
<br> | <br> | ||
Man kan sette inn den verdi man ønsker for radien r og derved få arealet A for en hvilket som helst radius.<br> | Man kan sette inn den verdi man ønsker for radien r og derved få arealet A for en hvilket som helst radius.<br> | ||
Bokstaver gir en formel som er allmenngyldig mens aritmetikken (tallregning)fokuserer på en eller flere spesielle tallverdier. | Bokstaver gir en formel som er allmenngyldig mens aritmetikken (tallregning) fokuserer på en eller flere spesielle tallverdier. | ||
====Variabel==== | |||
Et symbol, ofte x, y eller z , som representerer en verdi (et tall) som kan endre seg. | |||
\[2x +1 =5 \] | |||
I uttrykket over har x verdien 2. I uttrykket nedenfor har x verdien 5. | |||
\[2x + 1 = 11 \] | |||
I utrykket y = x + 1 har vi to variabler, x og y. Vi ser at det kan være mange tallpar som passer (et tallpar er to tall som i et gitt tilfelle passer sammen). Dersom man velger x = 1 blir y = 2. Velger jeg x= 52 blir y = 53. | |||
*x er en '''uavhengig variabel''' (kan velges) | |||
*y er en '''avhengig variabel''', gitt når x er valgt | |||
* (x,y) representer et tallpar, x og y hører sammen (i en gitt situasjon) | |||
====Konstant==== | |||
Tallet $\pi$ er en konstant. Det endrer seg aldri (3,1415....). | |||
====Parameter==== | |||
En parameter er symbolet for en verdi som er ''' fast i en gitt situasjon (konstant)'''. Vi regner tyngdens akselerasjon som en konstant så lenge vi befinner oss på jorden (g = 9,81 m/s^2). Dersom vi skal modellere krefter på månen eller andre himmellegemer kan man oppfatte g som en parameter, fordi tyngdens akselerasjon på månen er en annen enn på jorden. | |||
==== Ledd ==== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
Utrykk der tall eller / og bokstaver er adskilt med pluss eller minus | |||
\[a + b - 4 \] | |||
Uttrykket består av tre ledd, a, b og 4. | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
\[10a^2 + 2b + 2 \cdot 2 \] | |||
er også et uttrykk som består av tre ledd der hvert av leddene er produkter av to eller flere faktorer. | er også et uttrykk som består av tre ledd der hvert av leddene er produkter av to eller flere faktorer. | ||
== Produkt == | </div> | ||
==== Produkt ==== | |||
| Linje 40: | Linje 75: | ||
== Regneregler == | ==== Regneregler ==== | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Kommutativ lov:'''<p></p> | |||
\[a + b = b + a \] | |||
\[ab = ba\] | |||
Gjelder for addisjon og multiplikasjon. Rekkefølgen på tallene spiller ingen rolle. '''NB: Gjelder IKKE for subtraksjon og divisjon'''. | |||
'''Assosiativ lov:''' <p></p> | |||
\[(a + b) + c = a + (b + c)\] | |||
\[(a \cdot b) \cdot c = a \cdot (b \cdot c) \] | |||
Gjelder også for addisjon og multiplikasjon. Hvordan tallene grupperes spiller ingen rolle. | |||
'''Distributiv lov''' | |||
Sier at multiplikasjon kan "fordeles" over et parantesuttrykk. | |||
\[ a(b + c) = ab + ac \] | |||
Når vi faktoriserer går vi motsatt vei: | |||
\[ab + ac = a(b + c) \] | |||
</div> | |||
====Summering av bokstavuttrykk==== | |||
Alle like bokstavuttrykk legges sammen. Vi må behandle hvert bokstavuttrykk for seg. Alle a kan summeres for seg, alle ab for seg, alle x for seg osv. | |||
\[x + x + x = 3x \] | |||
Her er bare en type bokstav, x, og vi summerer antallet. | |||
\[x+ 2y -3x +y +4x = 2x + 3y\] | |||
Her legger vi sammen x for seg og y for seg. | |||
[ | \[xy + xy + x + y +x - y = 2x + 2xy\] | ||
xy må legges sammen for seg og kan ikke sumerers verken med x eller y. | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85F%2B860%2B861%2B862%2B863%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
==== Kvadratsetningene ==== | |||
De neste tre setningen kalles for kvadratsetningene. | |||
< | ==== Første kvadratsetning ==== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
== | \[(a+b)^2 = (a+b)(a+b)= a^2+2ab+b^2 \] | ||
< | </div> | ||
[[Bilde: | [[Bilde:Forste.png|centre]] | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel:''' <br> | '''Eksempel:''' <br> | ||
\[(3x+y)^2 = (3x+y)(3x+y)= 9x^2 + 6xy + y^2 \] | |||
</div> | |||
Det er nyttig å kunne regne ut kvadratet på denne måten når du skal forenkle utrykke ved å trekke sammen ledd. Man må også beherske kvadratsetningene andre veien, det er nødvendig ved forkorting av brøker. For å kunne forkorte et utrykk må det være på faktorform. Dette krever litt trening i å "se" hva produktet blir. | Det er nyttig å kunne regne ut kvadratet på denne måten når du skal forenkle utrykke ved å trekke sammen ledd. Man må også beherske kvadratsetningene andre veien, det er nødvendig ved forkorting av brøker. For å kunne forkorte et utrykk må det være på faktorform. Dette krever litt trening i å "se" hva produktet blir. | ||
< | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel:''' <br> | '''Eksempel:''' <br> | ||
\[ 16a^2 + 24ab + 9b^2 = (4a + 3b)^2 \] | |||
</div> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85F%2B860%2B861%2B862%2B863%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
==== Andre kvadratsetning ==== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
\[(a - b)^2 = (a - b)(a-b)= a^2-2ab+b^2 \] | |||
</ | </div> | ||
[[Bilde:Andre.png|centre]] | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel:''' <br> | |||
< | \[(3x-y)^2 = (3x-y)(3x-y)= 9x^2 - 6xy + y^2 \] | ||
</div> | |||
Det er nyttig å kunne regne ut kvadratet på denne måten når du skal forenkle utrykke ved å trekke sammen ledd. Man må også beherske kvadratsetningene andre veien, det er nødvendig ved forkorting av brøker. For å kunne forkorte et utrykk må det være på faktorform. Dette krever litt trening i å "se" hva produktet blir. | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
< | '''Eksempel:''' <br> | ||
\[ 16a^2 - 24ab + 9b^2 = (4a - 3b)^2\] | |||
== | </div> | ||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85F%2B860%2B861%2B862%2B863%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
==== Konjugatsetningen ==== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
\[(a + b)(a - b) = a^2 - b^2 \] | |||
</div> | |||
[[Bilde:Tredje.png|center]] | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel''' | |||
\[(5 + 2x)(5 - 2x) = 5^2 - 10x + 10x - 4x^2 = 25-4x^2 \] | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel''' | |||
\[9x^2 - 36y^2 = (3x+6y)(3x-6y) \] | |||
</div> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85F%2B860%2B861%2B862%2B863%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
====Faktorisering==== | |||
===== Tall ===== | |||
Alle tall større enn 1 kan skrives entydig som produktet av primtall. Eksempelvis kan tallet 52 skrives som 2· 2· 13 | |||
Faktorisering av tall går altså ut på å skrive tall som produkt av primtall. | |||
===== Bokstavuttrykk ===== | |||
$ 2a^3b - 4ab $ er et bokstavuttrykk som består av to ledd. Uttrykket kan faktoriseres ved å sette de faktorer som er felles i alle ledd utenfor en parentes: | |||
\[ 2\cdot a \cdot a \cdot a \cdot b - 2 \cdot 2 \cdot a \cdot b = 2ab(a^2 - 2)\] | |||
== Forkorting av brøkuttrykk == | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel:'''<br> | |||
\[ \frac {a^2}{ab}=\frac {\cancel{a} \cdot a }{\cancel{a} \cdot b} = \frac ab\] | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel''' | |||
\[ \frac {a^2}{a^3} = \frac{\cancel{a} \cdot \cancel{a} \cdot 1}{\cancel{a} \cdot \cancel{a} \cdot a} = \frac 1a\] | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel ''' | |||
\[ \frac {b}{b} = \frac{\cancel{b} \cdot 1}{\cancel{b} \cdot 1}\ = 1 \] | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel''' | |||
\[ \frac {(x+2)(x-2)}{(x+2)x}= \frac {\cancel{(x+2)}(x-2)}{\cancel{(x+2)}x}= \frac{x-2}{x} \] | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel''' | |||
\[ \frac {x^2 - 6x + 9}{2x^2 - 18}= \frac {(x-3)^2}{2(x+3)(x-3)}= \frac {\cancel{(x-3)}(x-3)}{2(x+3) \cancel{(x-3)}} = \frac{x-3}{2(x+3)}\] | |||
</div> | |||
[[Kategori:Algebra]] [[Kategori:1T]][[Kategori:2P]] | [[Kategori:Algebra]] [[Kategori:1T]][[Kategori:2P]] | ||
Siste sideversjon per 26. jun. 2025 kl. 04:11
Innledning
Det er ikke noe mystisk med bokstaver i et utrykk. En bokstav står for en spesiell tallverdi.

I linje to er det en rød firkant. Dersom likheten skal være riktig må verdien til firkanten være lik 1. I linje tre og fire er denne verdien byttet ut med bokstaver. For at linje 3 og 4 skal være riktige må både x og b ha verdien 1.
Algebra, eller bokstavregning, viser generelle sammenhenger. Tallregning eller aritmetikk gir oss mer spesielle sammenhenger.
En sirkel har radius 10 cm. Hva er arealet av sirkelen?
Arealet blir:
\[A = 10cm \cdot 10cm \cdot {\pi} =314,2 cm^2.\]
Men, det gjelder bare når radius i sirkelen er 10 cm. For alle andre radier er dette arealet feil.
Et areal som gjelder for en sirkel, uansett radius:
\[A = {\pi}r^2\]
Man kan sette inn den verdi man ønsker for radien r og derved få arealet A for en hvilket som helst radius.
Bokstaver gir en formel som er allmenngyldig mens aritmetikken (tallregning) fokuserer på en eller flere spesielle tallverdier.
Variabel
Et symbol, ofte x, y eller z , som representerer en verdi (et tall) som kan endre seg. \[2x +1 =5 \] I uttrykket over har x verdien 2. I uttrykket nedenfor har x verdien 5. \[2x + 1 = 11 \]
I utrykket y = x + 1 har vi to variabler, x og y. Vi ser at det kan være mange tallpar som passer (et tallpar er to tall som i et gitt tilfelle passer sammen). Dersom man velger x = 1 blir y = 2. Velger jeg x= 52 blir y = 53.
- x er en uavhengig variabel (kan velges)
- y er en avhengig variabel, gitt når x er valgt
- (x,y) representer et tallpar, x og y hører sammen (i en gitt situasjon)
Konstant
Tallet $\pi$ er en konstant. Det endrer seg aldri (3,1415....).
Parameter
En parameter er symbolet for en verdi som er fast i en gitt situasjon (konstant). Vi regner tyngdens akselerasjon som en konstant så lenge vi befinner oss på jorden (g = 9,81 m/s^2). Dersom vi skal modellere krefter på månen eller andre himmellegemer kan man oppfatte g som en parameter, fordi tyngdens akselerasjon på månen er en annen enn på jorden.
Ledd
Utrykk der tall eller / og bokstaver er adskilt med pluss eller minus
\[a + b - 4 \]
Uttrykket består av tre ledd, a, b og 4.
\[10a^2 + 2b + 2 \cdot 2 \]
er også et uttrykk som består av tre ledd der hvert av leddene er produkter av to eller flere faktorer.
Produkt
Av og til skrives ikke multiplikasjonstegnet mellom faktorene; a•b skrive ofte som ab og g•(h+f) skrives gjerne som g(h+f). Selv om man ikke skriver multiplikasjonstegnet er det der allikevel.
Når man regner med tall og parenteser har man muligheten til å trekke sammen parentesene før man løser de opp, i algebra er denne muligheten begrenset da man ikke uten videre kan trekke sammen for eksempel a + b. Før du går løs på regning med bokstaver er det derfor viktig at du kjenner reglene for regning med parenteser.
Alle regneregler du kjenner fra tallregning gjelder også for algebra. La oss se på noen regler:
Regneregler
\[a + b = b + a \] \[ab = ba\]
Gjelder for addisjon og multiplikasjon. Rekkefølgen på tallene spiller ingen rolle. NB: Gjelder IKKE for subtraksjon og divisjon.
\[(a + b) + c = a + (b + c)\] \[(a \cdot b) \cdot c = a \cdot (b \cdot c) \]
Gjelder også for addisjon og multiplikasjon. Hvordan tallene grupperes spiller ingen rolle.
Distributiv lov
Sier at multiplikasjon kan "fordeles" over et parantesuttrykk.
\[ a(b + c) = ab + ac \]
Når vi faktoriserer går vi motsatt vei: \[ab + ac = a(b + c) \]
Summering av bokstavuttrykk
Alle like bokstavuttrykk legges sammen. Vi må behandle hvert bokstavuttrykk for seg. Alle a kan summeres for seg, alle ab for seg, alle x for seg osv.
\[x + x + x = 3x \]
Her er bare en type bokstav, x, og vi summerer antallet.
\[x+ 2y -3x +y +4x = 2x + 3y\]
Her legger vi sammen x for seg og y for seg.
\[xy + xy + x + y +x - y = 2x + 2xy\]
xy må legges sammen for seg og kan ikke sumerers verken med x eller y.
Kvadratsetningene
De neste tre setningen kalles for kvadratsetningene.
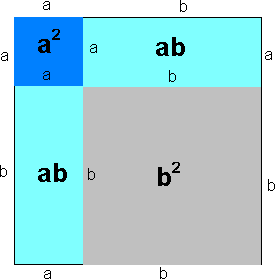
Første kvadratsetning
\[(a+b)^2 = (a+b)(a+b)= a^2+2ab+b^2 \]
Eksempel:
\[(3x+y)^2 = (3x+y)(3x+y)= 9x^2 + 6xy + y^2 \]
Det er nyttig å kunne regne ut kvadratet på denne måten når du skal forenkle utrykke ved å trekke sammen ledd. Man må også beherske kvadratsetningene andre veien, det er nødvendig ved forkorting av brøker. For å kunne forkorte et utrykk må det være på faktorform. Dette krever litt trening i å "se" hva produktet blir.
Eksempel:
\[ 16a^2 + 24ab + 9b^2 = (4a + 3b)^2 \]
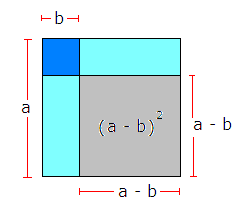
Andre kvadratsetning
\[(a - b)^2 = (a - b)(a-b)= a^2-2ab+b^2 \]
Eksempel:
\[(3x-y)^2 = (3x-y)(3x-y)= 9x^2 - 6xy + y^2 \]
Det er nyttig å kunne regne ut kvadratet på denne måten når du skal forenkle utrykke ved å trekke sammen ledd. Man må også beherske kvadratsetningene andre veien, det er nødvendig ved forkorting av brøker. For å kunne forkorte et utrykk må det være på faktorform. Dette krever litt trening i å "se" hva produktet blir.
Eksempel:
\[ 16a^2 - 24ab + 9b^2 = (4a - 3b)^2\]
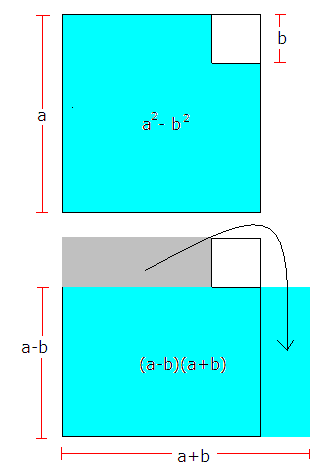
Konjugatsetningen
\[(a + b)(a - b) = a^2 - b^2 \]
Eksempel \[(5 + 2x)(5 - 2x) = 5^2 - 10x + 10x - 4x^2 = 25-4x^2 \]
Eksempel \[9x^2 - 36y^2 = (3x+6y)(3x-6y) \]
Faktorisering
Tall
Alle tall større enn 1 kan skrives entydig som produktet av primtall. Eksempelvis kan tallet 52 skrives som 2· 2· 13
Faktorisering av tall går altså ut på å skrive tall som produkt av primtall.
Bokstavuttrykk
$ 2a^3b - 4ab $ er et bokstavuttrykk som består av to ledd. Uttrykket kan faktoriseres ved å sette de faktorer som er felles i alle ledd utenfor en parentes:
\[ 2\cdot a \cdot a \cdot a \cdot b - 2 \cdot 2 \cdot a \cdot b = 2ab(a^2 - 2)\]
Forkorting av brøkuttrykk
Eksempel:
\[ \frac {a^2}{ab}=\frac {\cancel{a} \cdot a }{\cancel{a} \cdot b} = \frac ab\]
Eksempel \[ \frac {a^2}{a^3} = \frac{\cancel{a} \cdot \cancel{a} \cdot 1}{\cancel{a} \cdot \cancel{a} \cdot a} = \frac 1a\]
Eksempel
\[ \frac {b}{b} = \frac{\cancel{b} \cdot 1}{\cancel{b} \cdot 1}\ = 1 \]
Eksempel \[ \frac {(x+2)(x-2)}{(x+2)x}= \frac {\cancel{(x+2)}(x-2)}{\cancel{(x+2)}x}= \frac{x-2}{x} \]
Eksempel \[ \frac {x^2 - 6x + 9}{2x^2 - 18}= \frac {(x-3)^2}{2(x+3)(x-3)}= \frac {\cancel{(x-3)}(x-3)}{2(x+3) \cancel{(x-3)}} = \frac{x-3}{2(x+3)}\]