R2 2012 vår LØSNING: Forskjell mellom sideversjoner
m Teksterstatting – «</tex>» til «</math>» |
Ingen redigeringsforklaring |
||
| (26 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
{{EksLenker|1= | |||
*[http://www.matematikk.net/res/eksamen/R2/sensur/2012V_Vurderingsskjema_REA3024_Matematikk_R2_V12.pdf Vurderingsskjema] | |||
*[http://www.matematikk.net/res/eksamen/R2/sensur/2012V_Sensorveiledning_REA3024_Matematikk_R2_V12.pdf Sensorveiledning] | |||
*[http://www.ulven.biz/r2/eksamen/R2_V12_ls.pdf Alternativt løsningsforslag fra H-P Ulven] | |||
}} | |||
= Del 1 = | |||
== | == Oppgave 1 == | ||
=== a) === | |||
== | ''' 1) ''' $ f(x) = 3\sin 2x \\ u=2x, \quad u' = 2 \\ f'(x) = 2 \cdot 3 \cos 2x \\ f'(x) = 6\cos 2x$ | ||
=== | ''' 2) ''' $g(x) = x^2\sin x \\ u= x^2, \quad v = \sin x \\ g'(x) = 2x\sin x + x^2\cos x =x(2\sin x+x\cos x)$ | ||
''' 3) ''' $k(x) = 5\cos(\frac{\pi}{12}x-2)+7 \\ k'(x) = - \frac{5\pi}{12} \sin(\frac{\pi}{12}x-2)$ | |||
=== b) === | === b) === | ||
$\int xe^{2x}dx = \frac12 x e^{2x} - \int \frac12 e^{2x}dx \\ = \frac 12 x e^{2x} - \frac 14 e^{2x} +C \\ = \frac 14 e^{2x}(2x-1) + C$ | |||
=== c) === | === c) === | ||
$\int^7_3 \frac{2x}{x^2-4}dx \\ \frac{2x}{x^2+4} = \frac{A}{x-2}+ \frac{B}{x-2} \\ 2x= A(x+2) + B(x-2) \\ x=2 \Rightarrow A = 1 \\ x= -2 \Rightarrow B=1 \\ \int^7_3 \frac{2x}{x^2-4}dx =\int^7_3 \frac{1}{x-2}dx + \int^7_3 \frac {1}{x+2}dx \\ = [\ln|x-2|]^7_3 + [\ln|x+2|]^7_3 \\ = \ln5-\ln1+\ln9-\ln5 = \ln3^2 = 2\ln3$ | |||
=== d) === | === d) === | ||
$y' -2y = 3 \\ y' \cdot e^{-2x}-2ye^{-2x} = 3e^{-2x} \\ (ye^{-2x})' =3e^{-2x} \\ ye^{-2x} = - \frac 32 e^{-2x} + C \\ y = - \frac 32 +Ce^{2x} \\y(0) = 8 \Rightarrow 8 = - \frac 32 + C \Rightarrow C = \frac{19}{2} \\ y = - \frac 32 + \frac{19}{2}e^{2x}$ | |||
=== e) === | === e) === | ||
$1+e^{-x} + e^{-2x}+ .... \quad x > 0$ | |||
''' 1) ''' $k= \frac{e^{-x}}{1} = \frac{e^{-2x}}{e^{-x}} = e^{-x}$ <p></p> $ -1 < e^{-x}<1 $ Dvs: rekken konvergerer. | |||
< | |||
''' 2) ''' $S = \frac{a_1}{1-k} = \frac{1}{1-e^{-x}} = \frac {e^x}{e^x -1}$ | |||
== Oppgave 2 == | == Oppgave 2 == | ||
=== a) === | |||
$\vec{a}\cdot \vec{b} = [3,-1,2]\cdot [6,4,2]=3\cdot 6 - 1\cdot 4+2\cdot 2 = 18-4+4=18$ | |||
=== b) === | === b) === | ||
$\vec{a}\times \vec{b} = [-2-8, -(6-12), 12+6]=[-10,6,18]$ | |||
=== c) === | === c) === | ||
$\vec{a}-\vec{b}=[3,-1,2]-[6,4,2]=[-3,-5,0]$. Så $(\vec{a}-\vec{b})\cdot \vec{a}=[-3,-5,0]\cdot [3,-1,2]=-9+5=-4$ | |||
== Oppgave 3 == | == Oppgave 3 == | ||
$f(x) = x \cdot e^x$ | |||
=== a) === | === a) === | ||
$f'(x) = e^x +xe^x = (x+1)e^x \\ f´´(x) = e^x + (x+1)e^x = (x+2)e^x$ | |||
=== b) === | === b) === | ||
Ekstremalpunkter er gitt ved å nullstille den deriverte, altså løse $f'(x)=(x+1)e^x=0$. Siden eksponentialfunksjonen aldri er $0$, må $x+1=0$, som gir bunnpunkt i $x=-1$ siden den dobbeltderiverte er positiv i $x=-1$.Koordinatet til vendepunktet blir $(-1, f(-1)) =(-1, -e^{-1})$. Vendepunkter finner vi fra nullpunktene til $f^{\prime\prime}(x)$, altså må vi løse $(x+2)e^x=0$, som har løsning $x=-2$. Koordinatet til vendepunktet blir derfor $(-2,f(-2))=(-2,-2 e^{-2})$. | |||
=== c) === | === c) === | ||
$ f^{(n)} (x) = (x+n) e^x \\ n = 1: \quad f'(x) = e^x + xe^x = (1+x)e^x$<p></p> Formelen stemmer for $n = 1$.<p></p> | |||
Setter n = k og undersøker om formelen stemmer for k + 1: <p></p> | Setter $n = k$ og undersøker om formelen stemmer for $k + 1$: <p></p> | ||
$f^{(k+1)} = ((x+k)e^x)' = (x+k)'e^x + (x+k)(e^x)' = (x+k+1)e^x$ <p></p> | |||
Man slutter av dette at formelen gjelder for alle naturlige tall. | Man slutter av dette at formelen gjelder for alle naturlige tall. | ||
= Del 2 = | |||
== Oppgave 4 == | |||
== | === a) === | ||
25.mars svarer til dag $85$ etter nyttår. Altså er $t=85$. Vi har at $f(85) = 19 -4\cos(\frac{\pi \cdot 85}{180}) \approx 18,65 $. Altså begynner det å mørkne ca. kl. 18:39 på kvelden den 25. mars, ifølge modellen. | |||
== | === b) === | ||
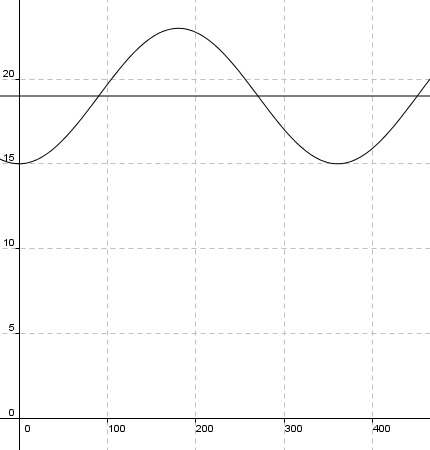
[[Fil:2012-r2-4b.png]] | [[Fil:2012-r2-4b.png]] | ||
Perioden er 360. | Grafisk ser vi at likevektslinjen er $19$. Den største verdien $f(t)$ kan ha er $23$, så amplituden blir $23-19=4$. Amplituden kan også finnes direkte fra funksjonsuttrykket som absoluttverdien til faktoren foran $\cos$. Perioden er $360=12\cdot 30$. Det gjennomsnittlige tidspunkt når lyset slåes på, gjennom hele året, er kl. 19:00. | ||
=== c) === | === c) === | ||
Dette kan leses direkte fra grafen. | |||
Dette kan leses direkte fra grafen. Vi ser fra grafen over at det er to løsninger. Disse kan regnes ut, slik: | |||
\begin{align*} | |||
f(t) & = 18 \\ | |||
Lyset slåes på kl. 18:00 16 mars og 16 september. | 19 - 4\cos( \frac{\pi \cdot t}{180}) & = 18 \\ | ||
t & =76 \quad \vee \quad t= 256 | |||
\end{align*} | |||
Lyset slåes på kl. 18:00 16. mars og 16. september. | |||
=== d) === | === d) === | ||
Dagslyset varer lengst i toppunktet til $f(t)$. Det svarer til at $\cos (\frac{\pi}{180}t)=-1$, altså når $\frac{\pi}{180}t = \pi$. Da er $t=180$, så dagslyset varer lengt midt i året, 30.juni. | |||
== Oppgave 5 == | == Oppgave 5 == | ||
| Linje 95: | Linje 114: | ||
=== a) === | === a) === | ||
\begin{align*} | |||
\tan(u-v) & = \frac{\sin(u-v)}{\cos(u-v)} \\ | |||
& = \frac{\sin u \cdot \cos v - \cos u\cdot \sin v }{\cos u \cdot \cos v + \sin u \cdot \sin v} \\ | |||
& = \frac{ \frac {\sin u \cdot \cos v}{\cos u \cdot \cos v} - \frac {\cos u \cdot \sin v}{\cos u \cdot \cos v} }{ \frac {\cos u \cdot \cos v}{\cos u \cdot \cos v} + \frac{\sin u \cdot \sin v}{\cos u \cdot \cos v}} \\ | |||
& = \frac{\tan u - \tan v}{1 + \tan u \cdot \tan v} | |||
\end{align*} | |||
=== b) === | |||
\begin{align*} | |||
f(x) & = \tan \alpha \\ | |||
&= \tan (u - v) \\ | |||
&= \frac{\tan u - \tan v}{1 + \tan u \cdot \tan v} \\ | |||
&= \frac{ \frac 4x - \frac 1x}{1 + \frac 4x \cdot \frac 1x} \\ | |||
&= \frac{4x-x}{x^2 + 4} \\ | |||
&= \frac{3x}{x^2 +4} | |||
\end{align*} | |||
=== c) === | === c) === | ||
<math>f'(x)= \frac{3(x^2+4)-3x \cdot 2x}{ (x^2+4)^2} = \frac{12-3x^2}{(x^2+4)^2} \\ f'(x)= 0 \Rightarrow 12-3x^2=0 \\ x= 2 | <math>f'(x)= \frac{3(x^2+4)-3x \cdot 2x}{ (x^2+4)^2} = \frac{12-3x^2}{(x^2+4)^2} \\ f'(x)= 0 \Rightarrow 12-3x^2=0 \\ x= 2 | ||
\\ f(2) = \frac 34</math> | \\ f(2) = \frac 34</math> | ||
=== d) === | === d) === | ||
<math>\frac 34 =tan | |||
Største synsvinkel:<p></p> | |||
<math>\frac 34 = \tan \alpha \\ \alpha = 36,9^{\circ}</math> | |||
== Oppgave 6 == | == Oppgave 6 == | ||
| Linje 113: | Linje 148: | ||
=== a) === | === a) === | ||
$v_0 = 25 \text{m/s} \\ y- \text{fart} \\y' - \text{akslerasjon} \\ \\ y' = ky^2 \\ \text{Bestemmer}\,k: \\ | |||
-12 = k \cdot25^2 \\ k = 0 | -12 = k \cdot25^2 \\ k = 0.02 \\ \\ \frac{dy}{dx} = -0,02y^2 \\ \int{y^{-2}}dy = \int -0,02dx \\ -y^{-1}= -0,02x + c \\ y= \frac{1}{0,02x+c}$ | ||
=== b) === | === b) === | ||
Ved tiden x = 0:<p></p> | Ved tiden $x = 0$:<p></p> | ||
$y = \frac 1C \\ 25 = \frac 1C \\ c = 0.04 $ | |||
<p></p> | <p></p> | ||
Farten til båten ved x = 3:<p></p> | Farten til båten ved $x = 3$:<p></p> | ||
$y(3) = \frac {1}{0.06 + 0.04} = 10 \text{m/s}$ | |||
=== c) === | === c) === | ||
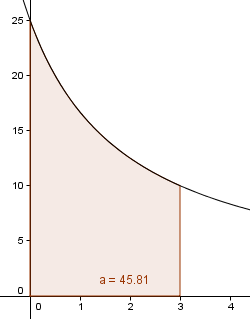
[[Fil:2012-r2-6c.png]]<p></p> | [[Fil:2012-r2-6c.png]]<p></p> | ||
Båten har forflyttet seg ca. 46 meter på 3 sekunder. | Båten har forflyttet seg ca. $46$ meter på $3$ sekunder. | ||
== Oppgave 7 == | == Oppgave 7 == | ||
=== a) === | |||
Teller vi opp antall kvadrater får vi $1+2+3+4+5=15$. Hvert kvadrat har areal $\frac{1}{5^2}$, så arealet av figuren er $\frac{15}{25}=\frac{3}{5}$. | |||
=== b) === | |||
I hver søyle er det $k$ antall kvadrater og hvert kvadrat har et areal $\frac{1}{n^2}$, så arealet av hele figuren blir $\sum_{k=1}^n k(\frac{1}{n})^2=\frac{1}{n^2}\sum_{k=!}^n k = \frac{1}{n^2}\frac{n(1+n)}{2}=\frac{1+n}{2n}$ | |||
En alternativ metode er å betrakte problemet geometrisk. Vi ser at arealet av figuren er halvparten av arealet til et kvadrat med sidelengder $1$ pluss halvparten av $n$ kvadrater med sidelengder $\frac{1}{n}$, altså er arealet av figuren $\frac12 + \frac12 \frac{n}{n^2}=\frac{1+n}{2n}$ | |||
Setter vi inn $n=5$ i summeformelen får vi $\frac{6}{10}=\frac{3}{5}$, som stemmer med utregningen i første deloppgave. | |||
=== c) === | |||
$\lim_{n\to\infty}S_n = \lim_{n\to\infty} \frac{1+n}{2n} =\lim_{n\to\infty}\frac{\frac1n + 1}{2} = \frac12$. | |||
Geometrisk ser vi at når $n$ vokser, så blir arealet av figuren tilnærmet halvparten av arealet av et kvadrat med sider $1$, altså $\frac12$. | |||
== Oppgave 8 == | == Oppgave 8 == | ||
=== a) === | |||
Punktene $A(0,0,4)$, $B(2,0,0)$ og $C(1,1,4)$ definerer et plan i $\mathbb{R}^3$. Vi starter med å beregne vektoren mellom punkt $A$ og $B$, som blir $B-A=[2,0,-4]$. Vektoren mellom punkt $A$ og $C$ blir $C-A=[1,1,0]$. Da har planet $\beta$ normalvektor $\vec{N}$ parallell med kryssproduktet mellom de to vektorene: | |||
\begin{equation*} | |||
\vec{N}=[2,0,-4]\times [1,1,0]=[4,-4,2] | |||
\end{equation*} | |||
$\beta$ er dermed gitt som alle punkter $(x,y,z)$ slik at | |||
\begin{align*} | |||
\left ([x,y,z]-A\right )\cdot \vec{N} & = 0 \\ | |||
\left ([x,y,z]-[0,0,4]\right )\cdot [4,-4,2] & = 0 \\ | |||
[x,y,z-4]\cdot [4,-4,2] & = 0 \\ | |||
4x-4y+2z -8 & = 0 \\ | |||
2x-2y+z -4 & = 0 | |||
\end{align*} | |||
Siden planene $\alpha$ og $\beta$ har parallelle normalvektorer, er planene parallelle. | |||
=== b) === | |||
Normalisert normalvektor for planene er $\frac{1}{\sqrt{2^2+2^2+1}}[2,-2,1]=\frac{1}{3}[2,-2,1]$.Vi vet at punktet $(0,0,4)$ ligger i planet $\beta$. Fra ligningen for planet $\alpha$ ser vi at punktet $(0,0,-2)$ ligger i $\alpha$. Vi beregner nå vektoren mellom disse to punktene: $[0,0,4]-[0,0,-2]=[0,0,6]$. Vektoren $[0,0,6]$ er altså en vektor mellom to punkter fra de to planene. Projiserer vi denne vektoren ned på enhetsnormalvektoren $\frac13 [2,-2,1]$ og tar absoluttverdien får vi avstanden mellom planene: | |||
\begin{equation*} | |||
|[0,0,6]\cdot \frac13[2,-2,1]|=|2|=2 | |||
\end{equation*} | |||
Avstanden mellom planene $\alpha$ og $\beta$ er derfor $2$. | |||
=== c) === | |||
Vi vet at normalvektoren til planene er parallell med linja $I$. Altså er $I$ parametrisert med parameter $t$ ved at $\vec{r}(t)=P+t[2,-2,1]=[5,-1,4]+[2t,-2t,t]=[5+2t,-1-2t,4+t]$. | |||
=== d) === | |||
$D$ ligger i planet $\alpha$, så vi må finne en $t$ slik at $(5+2t,-1-2t,4+t)$ tilfredsstiller ligningen for planet $\alpha$: $2x-2y+z+2=0$. Setter vi inn koordinatene i ligningen får vi at | |||
\begin{align*} | |||
2(5+2t)-2(-1-2t)+4+t+2 & = 0 \\ | |||
10+4t+2+4t+4+t+2 & = 0 \\ | |||
9t+18 &= 0 \\ | |||
t &=-2 | |||
\end{align*} | |||
Da blir $D(5-4, -1+4, 4-2)=D(1,3,2)$. Fremgangsmåten for å finne $E$ blir likedan. Vi må finne en $t$ slik at $(5+2t,-1-2t,4+t)$ tilfredsstiller ligningen for planet $\beta$: $2x-2y+z-4=0$: | |||
\begin{align*} | |||
2(5+2t)-2(-1-2t)+4+t-4 & = 0 \\ | |||
10+4t+2+4t+4+t-4 & = 0 \\ | |||
9t+12 &= 0 \\ | |||
t &=-\frac{4}{3} | |||
\end{align*} | |||
Vi får altså at $E(5-2\frac43, -1+2\frac43, 4-\frac43)=E(\frac73, \frac53,\frac83)$. | |||
=== e) === | |||
Kula har radius $1$, og senter i $(x_0,y_0,z_0)=\frac{D+E}{2}=(\frac53,\frac73,\frac73)$. Ligningen for kula er $(x-\frac53)^2+(y-\frac73)^2+(z-\frac73)^2=1$. | |||
Siste sideversjon per 24. mai 2015 kl. 08:50
Del 1
Oppgave 1
a)
1) $ f(x) = 3\sin 2x \\ u=2x, \quad u' = 2 \\ f'(x) = 2 \cdot 3 \cos 2x \\ f'(x) = 6\cos 2x$
2) $g(x) = x^2\sin x \\ u= x^2, \quad v = \sin x \\ g'(x) = 2x\sin x + x^2\cos x =x(2\sin x+x\cos x)$
3) $k(x) = 5\cos(\frac{\pi}{12}x-2)+7 \\ k'(x) = - \frac{5\pi}{12} \sin(\frac{\pi}{12}x-2)$
b)
$\int xe^{2x}dx = \frac12 x e^{2x} - \int \frac12 e^{2x}dx \\ = \frac 12 x e^{2x} - \frac 14 e^{2x} +C \\ = \frac 14 e^{2x}(2x-1) + C$
c)
$\int^7_3 \frac{2x}{x^2-4}dx \\ \frac{2x}{x^2+4} = \frac{A}{x-2}+ \frac{B}{x-2} \\ 2x= A(x+2) + B(x-2) \\ x=2 \Rightarrow A = 1 \\ x= -2 \Rightarrow B=1 \\ \int^7_3 \frac{2x}{x^2-4}dx =\int^7_3 \frac{1}{x-2}dx + \int^7_3 \frac {1}{x+2}dx \\ = [\ln|x-2|]^7_3 + [\ln|x+2|]^7_3 \\ = \ln5-\ln1+\ln9-\ln5 = \ln3^2 = 2\ln3$
d)
$y' -2y = 3 \\ y' \cdot e^{-2x}-2ye^{-2x} = 3e^{-2x} \\ (ye^{-2x})' =3e^{-2x} \\ ye^{-2x} = - \frac 32 e^{-2x} + C \\ y = - \frac 32 +Ce^{2x} \\y(0) = 8 \Rightarrow 8 = - \frac 32 + C \Rightarrow C = \frac{19}{2} \\ y = - \frac 32 + \frac{19}{2}e^{2x}$
e)
$1+e^{-x} + e^{-2x}+ .... \quad x > 0$
1) $k= \frac{e^{-x}}{1} = \frac{e^{-2x}}{e^{-x}} = e^{-x}$
$ -1 < e^{-x}<1 $ Dvs: rekken konvergerer.
2) $S = \frac{a_1}{1-k} = \frac{1}{1-e^{-x}} = \frac {e^x}{e^x -1}$
Oppgave 2
a)
$\vec{a}\cdot \vec{b} = [3,-1,2]\cdot [6,4,2]=3\cdot 6 - 1\cdot 4+2\cdot 2 = 18-4+4=18$
b)
$\vec{a}\times \vec{b} = [-2-8, -(6-12), 12+6]=[-10,6,18]$
c)
$\vec{a}-\vec{b}=[3,-1,2]-[6,4,2]=[-3,-5,0]$. Så $(\vec{a}-\vec{b})\cdot \vec{a}=[-3,-5,0]\cdot [3,-1,2]=-9+5=-4$
Oppgave 3
$f(x) = x \cdot e^x$
a)
$f'(x) = e^x +xe^x = (x+1)e^x \\ f´´(x) = e^x + (x+1)e^x = (x+2)e^x$
b)
Ekstremalpunkter er gitt ved å nullstille den deriverte, altså løse $f'(x)=(x+1)e^x=0$. Siden eksponentialfunksjonen aldri er $0$, må $x+1=0$, som gir bunnpunkt i $x=-1$ siden den dobbeltderiverte er positiv i $x=-1$.Koordinatet til vendepunktet blir $(-1, f(-1)) =(-1, -e^{-1})$. Vendepunkter finner vi fra nullpunktene til $f^{\prime\prime}(x)$, altså må vi løse $(x+2)e^x=0$, som har løsning $x=-2$. Koordinatet til vendepunktet blir derfor $(-2,f(-2))=(-2,-2 e^{-2})$.
c)
$ f^{(n)} (x) = (x+n) e^x \\ n = 1: \quad f'(x) = e^x + xe^x = (1+x)e^x$
Formelen stemmer for $n = 1$.
Setter $n = k$ og undersøker om formelen stemmer for $k + 1$:
$f^{(k+1)} = ((x+k)e^x)' = (x+k)'e^x + (x+k)(e^x)' = (x+k+1)e^x$
Man slutter av dette at formelen gjelder for alle naturlige tall.
Del 2
Oppgave 4
a)
25.mars svarer til dag $85$ etter nyttår. Altså er $t=85$. Vi har at $f(85) = 19 -4\cos(\frac{\pi \cdot 85}{180}) \approx 18,65 $. Altså begynner det å mørkne ca. kl. 18:39 på kvelden den 25. mars, ifølge modellen.
b)
Grafisk ser vi at likevektslinjen er $19$. Den største verdien $f(t)$ kan ha er $23$, så amplituden blir $23-19=4$. Amplituden kan også finnes direkte fra funksjonsuttrykket som absoluttverdien til faktoren foran $\cos$. Perioden er $360=12\cdot 30$. Det gjennomsnittlige tidspunkt når lyset slåes på, gjennom hele året, er kl. 19:00.
c)
Dette kan leses direkte fra grafen. Vi ser fra grafen over at det er to løsninger. Disse kan regnes ut, slik: \begin{align*} f(t) & = 18 \\ 19 - 4\cos( \frac{\pi \cdot t}{180}) & = 18 \\ t & =76 \quad \vee \quad t= 256 \end{align*} Lyset slåes på kl. 18:00 16. mars og 16. september.
d)
Dagslyset varer lengst i toppunktet til $f(t)$. Det svarer til at $\cos (\frac{\pi}{180}t)=-1$, altså når $\frac{\pi}{180}t = \pi$. Da er $t=180$, så dagslyset varer lengt midt i året, 30.juni.
Oppgave 5
a)
\begin{align*} \tan(u-v) & = \frac{\sin(u-v)}{\cos(u-v)} \\ & = \frac{\sin u \cdot \cos v - \cos u\cdot \sin v }{\cos u \cdot \cos v + \sin u \cdot \sin v} \\ & = \frac{ \frac {\sin u \cdot \cos v}{\cos u \cdot \cos v} - \frac {\cos u \cdot \sin v}{\cos u \cdot \cos v} }{ \frac {\cos u \cdot \cos v}{\cos u \cdot \cos v} + \frac{\sin u \cdot \sin v}{\cos u \cdot \cos v}} \\ & = \frac{\tan u - \tan v}{1 + \tan u \cdot \tan v} \end{align*}
b)
\begin{align*} f(x) & = \tan \alpha \\ &= \tan (u - v) \\ &= \frac{\tan u - \tan v}{1 + \tan u \cdot \tan v} \\ &= \frac{ \frac 4x - \frac 1x}{1 + \frac 4x \cdot \frac 1x} \\ &= \frac{4x-x}{x^2 + 4} \\ &= \frac{3x}{x^2 +4} \end{align*}
c)
<math>f'(x)= \frac{3(x^2+4)-3x \cdot 2x}{ (x^2+4)^2} = \frac{12-3x^2}{(x^2+4)^2} \\ f'(x)= 0 \Rightarrow 12-3x^2=0 \\ x= 2 \\ f(2) = \frac 34</math>
d)
Største synsvinkel:
<math>\frac 34 = \tan \alpha \\ \alpha = 36,9^{\circ}</math>
Oppgave 6
a)
$v_0 = 25 \text{m/s} \\ y- \text{fart} \\y' - \text{akslerasjon} \\ \\ y' = ky^2 \\ \text{Bestemmer}\,k: \\ -12 = k \cdot25^2 \\ k = 0.02 \\ \\ \frac{dy}{dx} = -0,02y^2 \\ \int{y^{-2}}dy = \int -0,02dx \\ -y^{-1}= -0,02x + c \\ y= \frac{1}{0,02x+c}$
b)
Ved tiden $x = 0$:
$y = \frac 1C \\ 25 = \frac 1C \\ c = 0.04 $
Farten til båten ved $x = 3$:
$y(3) = \frac {1}{0.06 + 0.04} = 10 \text{m/s}$
c)
Båten har forflyttet seg ca. $46$ meter på $3$ sekunder.
Oppgave 7
a)
Teller vi opp antall kvadrater får vi $1+2+3+4+5=15$. Hvert kvadrat har areal $\frac{1}{5^2}$, så arealet av figuren er $\frac{15}{25}=\frac{3}{5}$.
b)
I hver søyle er det $k$ antall kvadrater og hvert kvadrat har et areal $\frac{1}{n^2}$, så arealet av hele figuren blir $\sum_{k=1}^n k(\frac{1}{n})^2=\frac{1}{n^2}\sum_{k=!}^n k = \frac{1}{n^2}\frac{n(1+n)}{2}=\frac{1+n}{2n}$
En alternativ metode er å betrakte problemet geometrisk. Vi ser at arealet av figuren er halvparten av arealet til et kvadrat med sidelengder $1$ pluss halvparten av $n$ kvadrater med sidelengder $\frac{1}{n}$, altså er arealet av figuren $\frac12 + \frac12 \frac{n}{n^2}=\frac{1+n}{2n}$
Setter vi inn $n=5$ i summeformelen får vi $\frac{6}{10}=\frac{3}{5}$, som stemmer med utregningen i første deloppgave.
c)
$\lim_{n\to\infty}S_n = \lim_{n\to\infty} \frac{1+n}{2n} =\lim_{n\to\infty}\frac{\frac1n + 1}{2} = \frac12$.
Geometrisk ser vi at når $n$ vokser, så blir arealet av figuren tilnærmet halvparten av arealet av et kvadrat med sider $1$, altså $\frac12$.
Oppgave 8
a)
Punktene $A(0,0,4)$, $B(2,0,0)$ og $C(1,1,4)$ definerer et plan i $\mathbb{R}^3$. Vi starter med å beregne vektoren mellom punkt $A$ og $B$, som blir $B-A=[2,0,-4]$. Vektoren mellom punkt $A$ og $C$ blir $C-A=[1,1,0]$. Da har planet $\beta$ normalvektor $\vec{N}$ parallell med kryssproduktet mellom de to vektorene:
\begin{equation*} \vec{N}=[2,0,-4]\times [1,1,0]=[4,-4,2] \end{equation*}
$\beta$ er dermed gitt som alle punkter $(x,y,z)$ slik at
\begin{align*} \left ([x,y,z]-A\right )\cdot \vec{N} & = 0 \\ \left ([x,y,z]-[0,0,4]\right )\cdot [4,-4,2] & = 0 \\ [x,y,z-4]\cdot [4,-4,2] & = 0 \\ 4x-4y+2z -8 & = 0 \\ 2x-2y+z -4 & = 0 \end{align*}
Siden planene $\alpha$ og $\beta$ har parallelle normalvektorer, er planene parallelle.
b)
Normalisert normalvektor for planene er $\frac{1}{\sqrt{2^2+2^2+1}}[2,-2,1]=\frac{1}{3}[2,-2,1]$.Vi vet at punktet $(0,0,4)$ ligger i planet $\beta$. Fra ligningen for planet $\alpha$ ser vi at punktet $(0,0,-2)$ ligger i $\alpha$. Vi beregner nå vektoren mellom disse to punktene: $[0,0,4]-[0,0,-2]=[0,0,6]$. Vektoren $[0,0,6]$ er altså en vektor mellom to punkter fra de to planene. Projiserer vi denne vektoren ned på enhetsnormalvektoren $\frac13 [2,-2,1]$ og tar absoluttverdien får vi avstanden mellom planene:
\begin{equation*} |[0,0,6]\cdot \frac13[2,-2,1]|=|2|=2 \end{equation*}
Avstanden mellom planene $\alpha$ og $\beta$ er derfor $2$.
c)
Vi vet at normalvektoren til planene er parallell med linja $I$. Altså er $I$ parametrisert med parameter $t$ ved at $\vec{r}(t)=P+t[2,-2,1]=[5,-1,4]+[2t,-2t,t]=[5+2t,-1-2t,4+t]$.
d)
$D$ ligger i planet $\alpha$, så vi må finne en $t$ slik at $(5+2t,-1-2t,4+t)$ tilfredsstiller ligningen for planet $\alpha$: $2x-2y+z+2=0$. Setter vi inn koordinatene i ligningen får vi at
\begin{align*} 2(5+2t)-2(-1-2t)+4+t+2 & = 0 \\ 10+4t+2+4t+4+t+2 & = 0 \\ 9t+18 &= 0 \\ t &=-2 \end{align*}
Da blir $D(5-4, -1+4, 4-2)=D(1,3,2)$. Fremgangsmåten for å finne $E$ blir likedan. Vi må finne en $t$ slik at $(5+2t,-1-2t,4+t)$ tilfredsstiller ligningen for planet $\beta$: $2x-2y+z-4=0$:
\begin{align*} 2(5+2t)-2(-1-2t)+4+t-4 & = 0 \\ 10+4t+2+4t+4+t-4 & = 0 \\ 9t+12 &= 0 \\ t &=-\frac{4}{3} \end{align*}
Vi får altså at $E(5-2\frac43, -1+2\frac43, 4-\frac43)=E(\frac73, \frac53,\frac83)$.
e)
Kula har radius $1$, og senter i $(x_0,y_0,z_0)=\frac{D+E}{2}=(\frac53,\frac73,\frac73)$. Ligningen for kula er $(x-\frac53)^2+(y-\frac73)^2+(z-\frac73)^2=1$.