2P 2014 vår LØSNING

oppgaven som pdf

løsning 1 som pdf

løsning 2 som pdf

løsning 2 som LibreOffice Writer fil

løsning 2 GeoGebra-filer og regneark til løsningen

Oppgave 1

2, 5, 8, 10, 10, 15, 22, 28, 40, 50

Skriver tallene opp i stigende rekkefølge med tanke på median. Tall nummer fem er 10 og tall nummer seks er 15. Median bli gjennomsnittet av disse:

$\frac{10+15}{2}=12,5$

Median er 12,5

Gjennomsnitt: $\frac{2+5+8+10+10+15+22+28+40+50}{10}=19$

Gjennomsnittet er 19.

Variasjonsbredden er 50 - 2 = 48.

Oppgave 2

Får tallene på samme form.

$$\begin{gathered} (\frac{2}{3}{)}^2=\frac{4}{9} \\ (\frac{1}{4}{)}^0=1 \\ 6\cdot 2^{-3}=\frac{6}{8} \\ \frac{0,0016}{2\cdot {10}^{-3}}=\frac{16}{20}=\frac{8}{10} \end{gathered}$$

Fra minst til størst blir det: $\frac{4}{9},\frac{6}{8},\frac{8}{10},1$

eller

$(\frac{2}{3}{)}^2,6\cdot 2^{-3},\frac{0,0016}{2\cdot {10}^{-3}},(\frac{1}{4}{)}^0$

Dersom du synes dette er vannskelig å se kan du utvide brøkene slik at alle har samme nevner, da blir telleren avgjørende for størrelsen.

Oppgave 3

5 millioner = 5 000 000 = $5,0\cdot {10}^6$

150 milliarder = 150 000 000 000 = $1,5\cdot {10}^{11}$

$\frac{1,5\cdot {10}^{11}}{5,0\cdot {10}^6}$

Oppgave 4

$\frac{(2x{)}^4\cdot 2^{-1}}{8a^2}=\frac{2^4\cdot a^4\cdot 2^{-1}}{2^3\cdot a^2}=2^{4-1-3}\cdot a^{4-2}=a^2$

Oppgave 5

Man antar at resultatens fordeler seg jevnt utover intervallet i den enkelte klasse.

Poeng	Antall spillere, f	Klassemidtpunkt x	$x\cdot f$
[0, 40>	60	20	1200
[40, 80>	20	60	1200
[80, 120>	16	100	1600
[120, 180>	4	150	600
Total	100		4600

Gjennomsnitt: $\frac{4600}{100}=46$

Gjennomsnittet er 46 poeng.

Oppgave 6

Synnøve sykkler 6 km. Det bruker hun 20 munutter på, inkludert en pause på 4 minutter. Først sykkler hun, med jevn fart, 2 kilometer på 6 minutter. Det gir en fart på 20 km/h. (. ganger begge med 10) Hun har pause fra 6 til 10 minutter ute i turen. De siste 10 minuttene sykkler hun 4 km. med jevn hastighet. Om man ganger begge størrelsene med 6 finner man at dette gir en hastighet på 24 km/h.

Oppgave 7

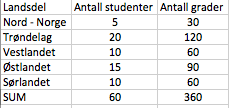
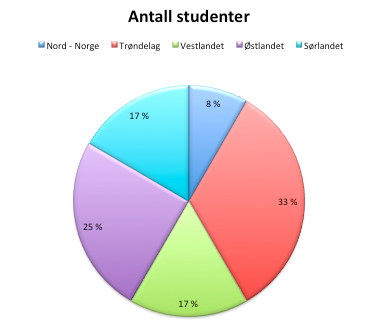
Dette er endel en oppgave og må gjøres med blyant, linjal og gradeskive. Vi har gjort den i Excel for at det skal se litt pent ut.

Det er 60 elever. I en sirkel er det 360 grader. En elev utgjør derfor 360 : 60 = 6 grader. Vi får da følgende tabell:

Oppgave 8

500 liter

2% forsvinner hvert år.

a)

Etter 12 år vil det være igjen:

$Igjen(12)=500\cdot 0,{98}^{12}$ liter.

b)

Det som har fordampet er forskjellen mellom det som var ved starten, og det som er igjen etter 20 år.

$Fordampet(20)=500-500\cdot 0,{98}^{20}$ liter

c)

2% av det som til enhver tid befinner seg på tønnen fordamper hvert år. Det første året fordamper 10 liter, da er det 490 liter igjen. 2% av 490 er mindre enn 10. Slik vil et stadig mindre og mindre volum fordampe, fordi det alltid er 2% av noe som blir mindre og mindre. Det vil være mere på tønna enn 250 liter etter 25 år.

Oppgave 9

a)

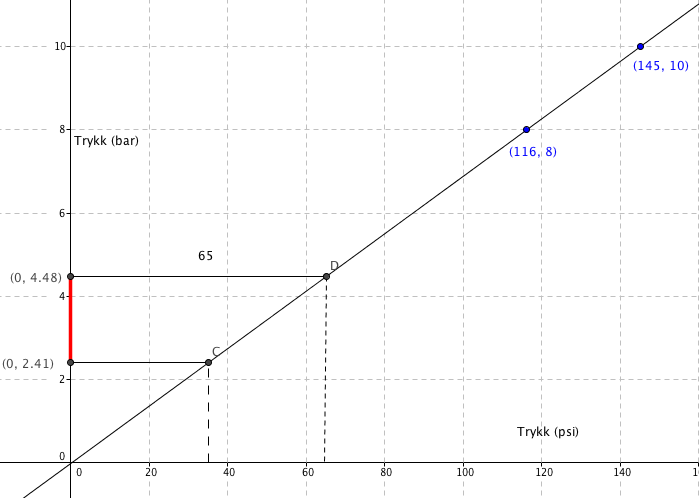
b)

Han bør ha mellom 2,4 og 4,5 bar i dekkene, avhengig av underlaget han skal sykkle på.

Oppgave 2

a)