S2 2015 vår LØSNING

Diskusjon av denne oppgaven

Oppgave 1

a)

$f^{\prime }(x)=e^{-2x}\cdot (-2)=-2e^{-2x}$

b)

Brukar brøkregelen med $u=x^2-1$ og $v=x$:

$$g^{\prime }(x)=\frac{u^{\prime }\cdot v-u\cdot v^{\prime }}{v^2}=\frac{2x\cdot x-(x^2-1)\cdot 1}{x^2}=\frac{2x^2-x^2+1}{x^2}=\frac{x^2+1}{x^2}$$

c)

Brukar produktregelen til å derivere $(3x+1)\cdot e^x$:

$h^{\prime }(x)=3\cdot e^x+(3x+1)\cdot e^x=(3x+4)e^x$

Oppgave 2

a)

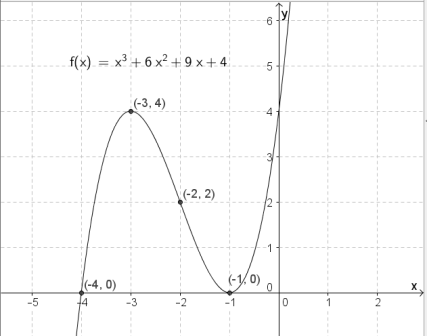
Jeg leser av nullpunktene på grafen:

$x=-3$, $x=-1$ og $x=3$.

Da vet vi at $(x+3)$, $(x+1)$ og $(x-3)$ er faktorer i polynomet $f(x)$.

$f(x)=(x+3)(x+1)(x-3)$

b)

Jeg bruker ett av nullpunktene, f.eks. $x=3$.

Vi vet at $f(x)=0$ for $x=3$:

$$\begin{gathered} f(3)=0 \\ {3}^3+3^2+k\cdot 3+k=0 \\ 27+9+3k+k=0 \\ 4k=-36 \\ k=-9 \end{gathered}$$

Oppgave 3

a)

En rekke er aritmetisk dersom differansen mellom et ledd og leddet foran er konstant.

$a_n-a_{n-1}=d$

b)

Av figuren ser vi at veggen er slik at $1$. rad (fra toppen) består av 1 murstein, 2. rad består av 2 murstein, 3. rad består av 3 murstein osv. Siste raden består av 20 murstein.

Summen av alle mursteinene blir da en aritmetisk rekke:

$1+2+3+\cdots +20$

Differansen $d$ mellom hvert ledd er 1. $a_1=1$ og $n=20$.

Vi bruker formelen for summen av en aritmetisk rekke:

$$\begin{gathered} S_n=\frac{a_1+a_n}{2}\cdot n \\ {S}_{20}=\frac{1+20}{2}\cdot 20=210 \end{gathered}$$

Mureren vil trenge 210 murstein til denne veggen.

Oppgave 4

a)

$$\begin{array}{rl}x& =0,555\dots \\ & =0,5+0,05+0,005+\dots \\ & =\frac{5}{10}+\frac{5}{100}+\frac{5}{1000}+\dots \\ & =\frac{5}{10}+\frac{5}{{10}^2}+\frac{5}{{10}^3}+\dots \end{array}$$

Dette er en geometrisk rekk med $k=\frac{1}{10}$ og $a_1=\frac{5}{10}$.

Siden $-1<k<1$, vil rekken konvergere med summen

$$\begin{gathered} s=\frac{a_1}{1-k} \\ x=\frac{\frac{5}{10}}{1-\frac{1}{10}}=\frac{\frac{5}{10}}{\frac{9}{10}}=\frac{5}{9} \end{gathered}$$

b)

$$\begin{array}{rl}y& =0,232323\dots \\ & =0,23+0,0023+0,000023+\dots \\ & =\frac{23}{100}+\frac{23}{10000}+\frac{23}{1000000}+\dots \\ & =\frac{23}{{10}^2}+\frac{23}{{10}^4}+\frac{23}{{10}^6}+\dots \end{array}$$

Dette er en geometrisk rekke med $k=\frac{1}{100}$ og $a_1=\frac{23}{100}$.

Siden $-1<k<1$, vil rekken konvergere med summen:

$$\begin{gathered} s=\frac{a_1}{1-k} \\ y=\frac{\frac{23}{100}}{1-\frac{1}{100}}=\frac{\frac{23}{100}}{\frac{99}{100}}=\frac{23}{99} \end{gathered}$$

Oppgave 5

a)

$f(-1)=(-1{)}^3+6\cdot (-1{)}^2+9\cdot (-1)+4=-1+6-9+4=0$

For å finne eventuelle andre nullpunkter kan vi bruke polynomdivisjon til å løse likningen $f(x)=0$.

Siden $f(x)=0$ for $x=-1$, vet vi at divisjonen $f(x):(x+1)$ går opp:

$(x^3+6x^2+9x+4):(x+1)=x^2+5x+4$

Bruker abc-formelen til å løse likningen $x^2+5x+4=0$:

$$\begin{gathered} x=\frac{-5\pm \sqrt{5^2-4\cdot 1\cdot 4}}{2}=\frac{-5\pm \sqrt{9}}{2}=\frac{-5\pm 3}{2} \\ x=-1\vee x=-4 \end{gathered}$$

Nullpunktene til $f$ er $x=-1$ og $x=4$.

b)

Grafen til $f$ har eventuelle topp- eller bunnpunkter der $f^{\prime }(x)=0$.

$f^{\prime }(x)=3x^2+12x+9=3(x^2+4x+3)$

Løser likningen $x^2+4x+3=0$:

$$\begin{gathered} x=\frac{-4\pm \sqrt{4^2-4\cdot 1\cdot 3}}{2\cdot 1}=\frac{-4\pm \sqrt{16-12}}{2}=\frac{-4\pm 2}{2} \\ x=-3\vee x=-1 \end{gathered}$$

$\Rightarrow f^{\prime }(x)=3(x+1)(x+3)$

Bruker det faktoriserte uttrykket til å tegne fortegnslinje for $f^{\prime }(x)$:

Av fortegnslinja ser vi at $f^{\prime }(x)$ skifter fortegn fra $+$ til $-$ i $x=-3$, og fra $-$ til $+$ i $x=-1$.

$$\begin{gathered} f(-3)=(-3{)}^3+6\cdot (-3{)}^2+9\cdot (-3)+4=-27+54-27+4=4 \\ f(-1)=0 \end{gathered}$$

Grafen til $f$ har et toppunkt i $(-3,4)$ og et bunnpunkt i $(-1,0)$.

c)

Grafen til $f$ har eventuelle vendepunkter der $f^{″}(x)=0$.

$f^{″}(x)=6x+12=6(x+2)$

$$\begin{gathered} 6(x+2)=0 \\ x=-2 \end{gathered}$$

Tegner fortegnslinje for $f^{″}(x)$:

Vi ser at $f^{″}(x)$ skifter fortegn når $x=-2$.

$f(-2)=(-2{)}^3+6\cdot (-2{)}^2+9\cdot (-2)+4=-8+24-18+4=2$

Grafen til $f$ har et vendepunkt i $(-2,2)$.

d)

Oppgave 6

a)

Summen av alle sannsynlighetsverdiene i en sannsynlighetsfordeling skal være lik 1.

Det gir oss første likning: $a+b+c=1$

Forventningsverdien regner vi ut slik: $\mu =E(X)=\sum x_i\cdot P(X=x_i)$ som gir:

$\mu =E(X)=0\cdot a+1\cdot b+2\cdot c=b+2c$

Det gir oss andre likning: $b+2c=\frac{1}{2}$

Variansen regner vi ut slik: $Var(X)=\sum (x_i-\mu {)}^2\cdot P(X=x_i)$ som gir:

$Var(X)=(0-\frac{1}{2}{)}^2\cdot a+(1-\frac{1}{2}{)}^2\cdot b+(2-\frac{1}{2}{)}^2\cdot c=\frac{1}{4}a+\frac{1}{4}b+\frac{9}{4}c$

Det gir oss tredje likning: $$\begin{gathered} \frac{1}{4}a+\frac{1}{4}b+\frac{9}{4}c=\frac{1}{2} \\ a+b+9c=2 \end{gathered}$$

b)

Jeg starter med andre likning: $b=\frac{1}{2}-2c$

Setter dette inn i første likning: $$\begin{gathered} a+\frac{1}{2}-2c+c=1 \\ a=\frac{1}{2}+c \end{gathered}$$

Setter inn i siste likning: $$\begin{gathered} (\frac{1}{2}+c)+(\frac{1}{2}-2c)+9c=2 \\ 8c=1 \\ c=\frac{1}{8} \end{gathered}$$

$$\begin{gathered} a=\frac{1}{2}+\frac{1}{8}=\frac{5}{8} \\ b=\frac{1}{2}-\frac{2}{8}=\frac{2}{8}=\frac{1}{4} \end{gathered}$$

Oppgave 7

a)

$x=90$ gir

$z=\frac{x-\mu }{\sigma }=\frac{90-100}{20}=\frac{-10}{20}=-\frac{1}{2}=-0,50$

Denne $z$-verdien kan vi slå opp i tabellen for standard normalfordeling:

$P(X\le 90)=P(Z\le -0,50)=0,3085$.

Sannsynligheten for at en tilfeldig valgt hjortebukk veier mindre enn 90 kg er ca. 31 %.

b)

$x=110$ gir:

$z=\frac{110-100}{20}=\frac{10}{20}=0,50$

$$\begin{gathered} P(90\le X\le 110)=P(-0,50\le Z\le 0,50) \\ =P(Z\le 0,50)-P(Z\le -0,50) \\ =0,6915-0,3085=0,3830 \end{gathered}$$

Sannsynligheten for at en tilfeldig valgt bukk veier mellom 90 og 110 kg er 38,3 %.

Oppgave 8

Jeg ser først på funksjonen $f$:

Når $x\to -\mathrm{\infty }$ vil $e^{-x}\to \mathrm{\infty }$.

Da vil $\frac{100}{1+e^{-x}}\to 0$ og $f(x)\to 0-25=-25$

Den eneste grafen som passer med dette er graf (4).

Nå ser vi på funksjonen $g$:

Når $x\to \mathrm{\infty }$ vil $e^{-(x-5)}\to 0$.

Da vil $g(x)\to \frac{100}{1+0}=100$

Den eneste grafen som flater ut ved 100, er graf (1).

Graf (4) hører til $f$, og graf (1) hører til $g$.

Oppgave 1

a)

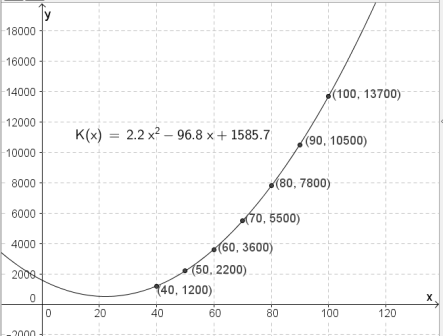
Jeg legger tabellen inn i regnearket i GeoGebra, høyreklikker og velger "Lag liste med punkt".

Så skriver jeg inn kommandoen "RegPoly[Liste1, 2]" siden oppgaven sier at vi skal finne et andregradsuttrykk.

Jeg får denne funksjonen:

$K(x)=2,2x^2-96,8x+1585,7$

b)

Overskuddet er størst når grenseinntekten er lik grensekostnaden.

Vi må altså finne $p$ slik at

$K^{\prime }(75)=I^{\prime }(75)$

Løser dette i CAS:

Overskuddet $O(x)=I(x)-K(x)$.

Dersom overskuddet skal bli størst mulig ved produksjon og salg av 75 enheter, må $p$ være 230.

Da er overskuddet 10669 kroner.

Oppgave 5

a)

Når grafen skjærer y-aksen, er $x=0$.

Regner ut $f(0)$:

$$f(0)=\frac{a}{1+b\cdot e^0}=\frac{a}{1+b}$$

b)

I vendepunktet er $f^{″}(x)=0$.

Jeg bruker CAS i GeoGebra til å løse likningen $f^{″}(x)=0$. Etterpå settter jeg løsningen inn i uttrykket for $f(x)$.

c)

Stigningstallet til tangenten i punktet $V$ er lik den deriverte av $f$ i punktet $V$.

Jeg regner ut $f^{\prime }(x)$, der jeg setter inn $x$-koordinaten til vendepunktet. (Som vi fant i oppg. b))